Для оценки состояния устойчивости откосов уступов и бортов разрезов на практике имеют наибольшее распространение следующие способы расчета:
− способ алгебраического сложения сил;
− графоаналитический способ (ВНИМИ).
В тех случаях, когда в массиве горных пород нет поверхностей ослабления, падающих в сторону выемки или горизонтальных, применяется схема расчета, характеризующаяся тем, что в этом случае поверхность скольжения можно принимать круглоцилиндрической, а коэффициент запаса устойчивости определять методом алгебраического сложения удерживающих и сдвигающих сил по этой поверхности.
Графоаналитический способ определения параметров устойчивых откосов (способ ВНИМИ) заключается в определении параметров предельного откоса (высота, угол наклона и ширина призмы возможного обрушения) по графикам Г. Л. Фисенко.
Широкое использование вычислительной техники потребовало разработки теоретически обоснованных численно- аналитических способов расчета, позволяющих исключить трудоемкие аналитические расчеты вручную и графические построения.
Массив горных пород является сложной физической средой, обладающей рядом специфических особенностей, которые во многом определяют его механическое состояние. Поэтому для математического описания происходящих в массиве процессов при разработке методов расчёта устойчивости откосов вынужденно прибегают к схематизации рассматриваемых явлений и свойств породного массива.

Рис. 1. Расчетная схема
В результате создается геомеханическая модель прибортового массива, приближенно отражающая действительную природу рассматриваемого процесса.
По мнению Г. Л. Фисенко геомеханическая модель строится на основе геологической модели для решения определённой проблемы определенными методами. Отличие расчётной модели от геологической состоит в том, что помимо геологических факторов она должна учитывать механизм того процесса, для изучения которого она предназначена, а также используемые при этом методы анализа. Одной из основных задач исследования механизма деформирования массива горных пород, является выявление формы и местоположения поверхности скольжения.
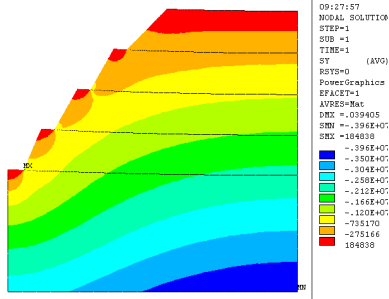
Рис. 2. Вертикальные напряжения
Для всего многообразия горно-геологических условий прибортового массива в результате проведённых исследований нами предлагается определение напряженно-деформированное состояния приоткосного массива, с применением численного метода конечных элементов.
Метод конечных элементов является численным методом решения дифференциальных уравнений, встречающихся в физике и технике.
Область применения метода конечных элементов существенно расширилась, когда было показано, что уравнения, определяющие элементы в задачах строительной механики, распространения тепла, гидромеханики, могут быть легко получены с помощью таких вариантов метода взвешенных невязок, как метод Галёркина или способ наименьших квадратов.
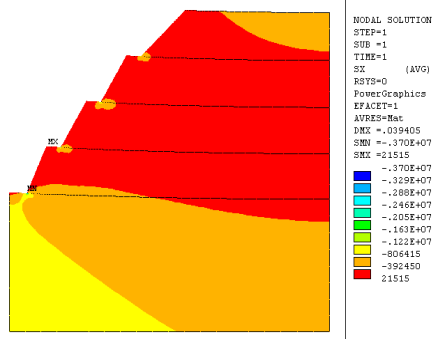
Рис. 3. Горизонтальные напряжения
Задачей исследований является определение параметров напряженно-деформированного (НДС) массива, влияющие на устойчивость бортов карьера. Рассматривается вертикальное сечение массива вокруг уступов.
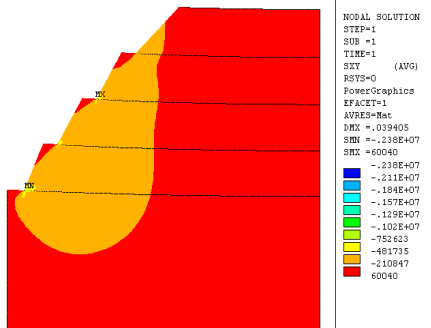
Рис. 4. Касательные напряжения
В качестве расчётной схемы выбрана прямоугольная плоскость, находящаяся в плоско деформированном состоянии и которая разбивается сеткой треугольных элементов, с соответствующими граничными условиями (рисунок 1).
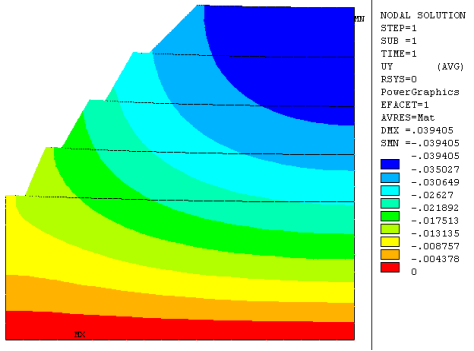
Рис. 5. Изолинии вертикальных смешений
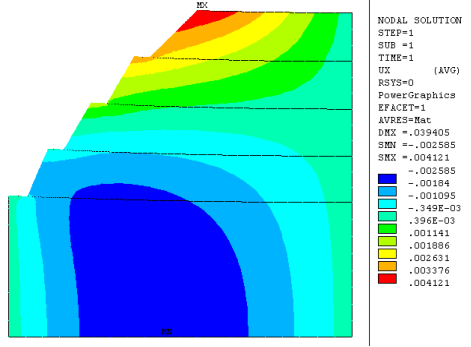
Рис. 6. Изолинии горизонтальных смещений
На расчётной схеме На границах АВ и СD отсутствуют горизонтальные, на АD вертикальные перемещения.
На рисунках 2–4 приведены изолинии горизонтальных, вертикальных и касательных напряжений для однородного массива горных пород т. е. при модуле упругости вмещающих пород Е =104 МПа, высота уступа — 30 м., плотность массива — 2000 кг/м3.
На рисунках 5 и 6 приведены изолинии вертикальных и горизонтальных смещений.
Литература:
- Ержанов Ж. С., Каримбаев Т. Д. Метод конечных элементов в задачах механики горных пород. — Алма-Ата: Наука, 1975. — 238 с.
- Тутанова М. С. Устойчивость карьерных бортов с учетом напряженно-деформированного состояния прибортового массива. «AKTUALNE PROBLEMY NOVOCZESNYCH NAUK — 2010», том 31, Przemysl Nauka 3 studia 2010. – C. 38–42.

