Применение автомата Мура для решения элементарных логических задач



В данной статье рассматривается создание автомата Мура на примере вычисления простейших логических операций. В ходе данной работы будет проведена оценка экономических затрат на построение схемы, а также оценку её быстродействия.

Принцип микропрограммного управления допускает, что цифровое устройство состоит из двух частей: операционного автомата (ОА) и управляющего автомата (УА) [1]. ОА выполняет элементарные операции (микрооперации) такие как сдвиг, алгебраическое сложение, конъюнкция и дизъюнкция. УА формирует последовательность управляющих сигналов, которые поступают к ОА и это даёт возможность реализовывать более сложные алгоритмы.

УА подразделяются на две большие группы: автоматы с жёсткой логикой и автоматы с программируемой логикой. В данной статье будет разработан автомат с жёсткой логикой. В свою очередь такие автоматы делятся на автоматы, выполненные по схеме Мили и по схеме Мура.

Для наглядного примера реализуем простейшую микропрограмму, выполняющую заданный порядок действий на основе входных данных. В качестве входных данных принимаются значения регистров RA, RB, RC которые задаются вручную до начала работы микропрограммы.

Опишем принцип работы микропрограммы. Общая схема приведена на рисунке 1.

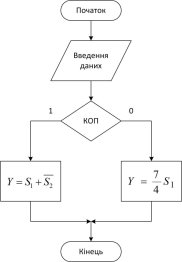
Рис. 1. Общий алгоритм вычисления формулы S

Возможны два варианта работы программы в зависимости от введённых данных. Если заданное условие выполняется, то необходимо вычислить аддитивный блок работы, иначе мультипликативный. Для вычисления блоков используются выражения S1 и S2, формулы для которых приведены ниже.

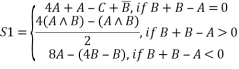
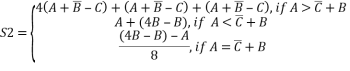
Функциональный алгоритм разработаем согласно входным данным. Сначала выполним загрузку входных данных в регистры RA, RB, RC. При составлении алгоритма необходимо уменьшить разнообразие команд, а также уменьшить количество операторных вершин. Из-за того, что невозможно загрузить за один такт работы данные сразу в три регистра, осуществим это за два такта. За первый так параллельно загрузим данные в регистры RA и RB с помощью шин Z₁ и Z₂, а за второй — в регистр RC через шину Z₁.

Далее необходимо построить операционный автомат. Чтобы построить структурную схему необходимо обозначить набор комбинационных схем: двуместные: {Sum, Sub, And}; одноместные: {Not, L2, L3, R1, R2, R3 }; распределить связи между регистра и локальными шинами А1, А2, А3: А1 = {RA, RB, RC, RD, RE}, А2 = {RA, RB, RD, RF, RE}, А3 = {RA, RB, RC, RD, RF, RE}; и обозначить обратные связи шин Z1 и Z2 с регистрами памяти: Z1 = {RA, RC, RD, RF, RE}, Z2 = {RB, RD, RF, RE}.

Каждое элементарное действие в схеме может выполняться только при наличии определённого управляющего сигнала yn (микрооперации):

y1–y3 — загрузка начальных данных на шины.

y4–y12 — загрузка данных в регистры памяти.

y13–y28 — загрузка из памяти на шины операндов А1, А2, А3.

y29–y31 — загрузка результатов двуместных операций на шину Z2.

y32–y37 — загрузка результатов двуместных операций на шину Z1.

Согласно с полученными данными формируем операционный автомат (Рис. 2).

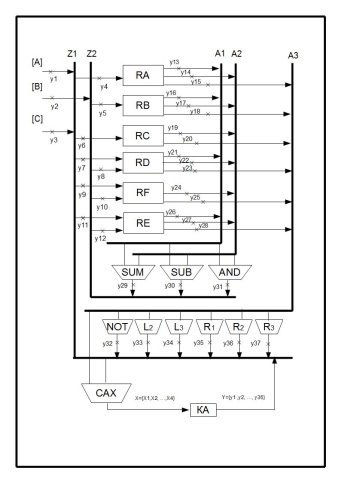
Рис. 2. Структурная схема операционного автомата

Шинный формирователь — это комбинационная схема, которая обеспечивает соответствие бита информации, который принимается на шину и проводника.

Формулы для i-го бита шинного формирователя Аі:

;

;

;

Формулы для i-го бита шинного формирователя Zi:

;

;

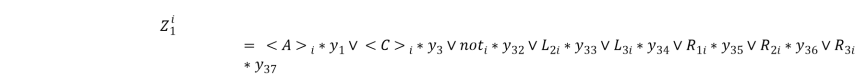Формулы для i-го бита шинного формирователя в заданном базисе:

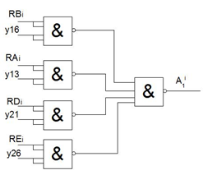
Рис. 3. Фрагмент схемы шинного формирователя

В результате получаем граф-схему алгоритма вычисления формулы S. Она служит начальными данными для синтеза управляющего автомата.

После создания граф-схемы алгоритма вычисления заданных формул, синтеза шинного формирователя и построения операционного автомата приступим к разработке управляющих автоматов. Один из автоматов будет построен на принципе конечного автомата Мура, другой — Мили.

Порядок синтеза автомата Мура [2]:

На первом этапе начальная и конечная вершины обозначаются одним состоянием. Затем отдельным состоянием обозначается вход каждой операторной вершины.

Построение таблицы переходов сводится к формированию по обозначенной ГСА таблицы, которая содержит столбцы:

a_m — начальное состояние

k(a_m) — код начального стостояния

a_s — следующее состояние

k(a_s) — код следующего состояния

X — логическое условие, при котором выполянется переход

Y — мокрокоманды, которые выполняются при переходе

F — функции возбуждения памяти

При кодировании состояний необходимо стараться уменьшить количество функция возбуждения, которые принимают единичное значение.

Построим таблицу дла автомата Мура (Табл. 1), проверка RD=0 обозначена как Х1, проверка RD<0 обозначена как Х2, код операции (КОП) — как Х3, проверка RA

Таблица 1

Прямая структурная таблица для автомата Мура

am	K(am)	as	K(as)	X	Y	F
a0	00000	a1	00001	1	-	S0
a1	00001	a2	00010	1	y1, y2, y4, y5	S1 R0
a2	00010	a3	00011	1	y3, y6, y16, y17, y29, y10	S0
a3	00011	a4	00100		y13, y24, y30, y8	S2 R1 R0
		a7	00111	*		S2
		a1o	01010	*		S3 R0
a4	00100	a5	00101	1	y21, y19, y30, y8, y18, y32, y0	S0
a5	00101	a6	00110	1	y21, y24, y29, y8, y15, y33, y4	S1 R0
a6	00110	a14	01110		y21, y27, y29, y12	S3
		a16	10000			S4 R2 R1
a7	00111	a8	01000	1	y15, y34, y11	S3 R2 R1 R0
a8	01000	a9	01001	1	y16, y27, y29, y12, y18, y33, y7	S0
a9	01001	a14	01110		y26, y22, y30, y10	S1 S2 R0
		a16	10000			S4 R3 R0
a10	01010	a11	01011	1	y13, y17, y31, y10	S0
a11	01011	a12	01100	1	y25, y33, y9	S2 R1 R0
a12	01100	a13	01101	1	y21, y24, y30, y8	S0
a13	01101	a14	01110		y23, y35, y11	S1 R0
		a16	10000			S4 R3 R2 R0
a14	01110	a15	01111	1	y20, y32, y9	S0
a15	01111	a19	10011		y16, y24, y29, y10	S4 R3 R2
		a24	11000			S4 R2 R1 R0
a16	10000	a17	10001	1	y28, y34, y7	S0
a17	10001	a18	10010	1	y21, y27, y30, y6	S1 R0
a18	10010	a0	00000	1	y23, y36, y7	R4 R1
a19	10011	a20	10100	1	y18, y33, y7	S2 R1 R0
a20	10100	a21	10101		y21, y17, y30, y8	S0
		a22	10110			S1
a21	10101	a29	11101	1	y21, y14, y29, y6	S3
a22	10110	a23	10111	1	y21, y14, y29, y8	S0
a23	10111	a29	11101	1	y23, y37, y7	S3 R1
a24	11000	a25	11001	1	y13, y19, y30, y10, y18, y32, y7	S0
a25	11001	a26	11010	1	y21, y24, y29, y10	S1 R0
a26	11010	a27	11011	1	y25, y33, y7	S0
a27	11011	a28	11100	1	y21, y24, y29, y8	S2 R1 R0
a28	11100	a29	11101	1	y21, y24, y29, y8	S0
a29	11101	a30	11110	1	y23, y32, y7	S1 R0
a30	11110	a0	00000	1	y26, y22, y29, y8	R4 R3 R2 R1

Функции возбуждения памяти в заданном базисе:

Уравнения выходных сигналов в заданном базисе:

;; ; ;; ;

; ;

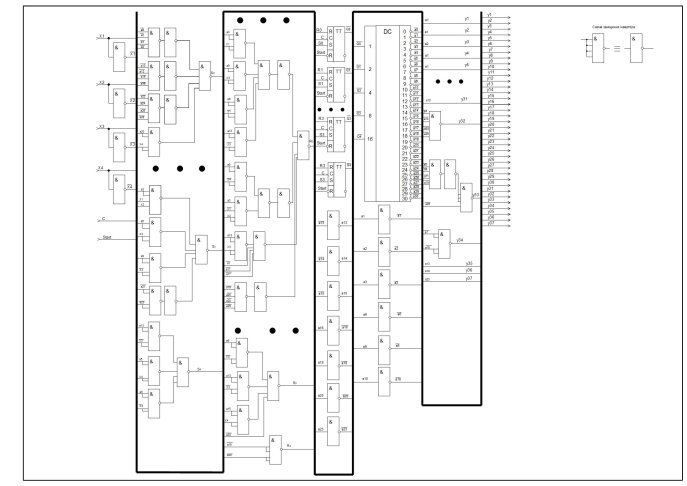
Рис.4. Сокращённая схема автомата Мура

Количество затраченных ресурсов на построение схемы составило 134 элемента. Исходя из того, что эти элементы имеют низкую себестоимость, можно сделать вывод, что схема обладает высокой экономической эффективностью, но низкой скоростью вычисления результата.

В дальнейшем эта же задача будет решена на автомате, спроектированном по принципу автомата Мили и проведено экономическое сравнение с данным автоматом.

Литература:

1. Баркалов А. А., Титаренко Л. А.. Прикладная теория цифровых автоматов.. — Донецк: ДонНТУ, Технопарк ДонНТУ УНИТЕХ, 2010. — 320 с.
2. Баркалов А. А., Титаренко Л. А.. Синтез операционных устройств. — Донецк: РВА ДонНТУ, 2003. — 306 с.