Исследование множественного рождения частиц в адрон-адронных столкновениях при высоких энергиях



Статья посвящена рассмотрению средней множественности заряжённых частиц при высоких энергиях и применению некоторых теоретических моделей к экспериментальным данным.

Ключевые слова: физика высоких энергий, инклюзивные процессы, масштабная инвариантность, адрон-адронные столкновения

На современном этапе развития физики высоких энергий изучение процессов множественного рождения частиц является одной из центральных проблем физики элементарных частиц.

В настоящее время, в основном, изучаются характеристики одной частицы или нескольких независимо от поведения других вторичных частиц (инклюзивные процессы). В работах, рассматривающих общие свойства инклюзивных реакций, показано, что при высоких энергиях в сильных взаимодействиях, возможно, имеет место так, например масштабная инвариантность [1]. Это принципиальный вопрос и ему посвящено большое число экспериментов.

В этой статье экспериментальные результаты по средней множественности заряженных частиц сравниваются с теоретическими моделями.

Как известно, что практически невозможно исследовать процессы множественного рождения с фиксированным числом вторичных частиц, как это было сделано при ( — энергия налетающей частицы в лабораторной системе координат). Аналогичная ситуация имеет место в отношении установления природы всех вторичных частиц. Имеется ряд теоретических моделей, которые рассматривают инклюзивные реакции и предсказывают основные их характеристики при высоких энергиях.

Основная идея применения статистики для вычисления характеристик множественных процессов впервые была высказана итальянским физиком Э.Ферми. В модели Ферми предполагалось, что в адрон-адронных столкновениях образуется единая компаунд — система, из которой должны вылететь, не взаимодействуя, все конечные частицы.

Новая модель стала широко применяться для объяснения экспериментальных данных при низких энергиях (), когда рождаются одна-две новые частицы.

В начале результаты имели хорошее согласие с предсказаниями статистической модели. Однако при переходе к большим обнаружилось несогласие экспериментальных данных с этой моделью. Главная причина заключается в том, что в подавляющем большинстве соударений отнюдь не справедлива основная гипотеза образования единой компаунд-системы. Налетающая частица обычно проскакивает вперед, отдавая на образование новых частиц лишь часть своей энергии («лидирующая частица»).

Далее выяснилось, что с ростом энергии первичной частицы, применимость модели Ферми ограничена событиями с большой множественностью вторичных частиц.

На основе модели Ферми, Померанчук и Ландау в одно и тоже время построили более современную статистическую модель [2].

Померанчук предполагал, что при соударении двух адронов образуется компаунд-система, а частицы взаимодействуют друг с другом до тех пор, пока температура системы не станет (- масса -мезона). При этом объём системы расширяется, а множественность частиц в конечном состоянии растет.

Основные выводы из статистической модели Ферми не согласуется на наблюдаемой, эксперименте анизотропией угловых распределений вторичных частиц, особенно нуклонов, постоянством полных сечений при высоких энергиях и малой величиной среднего поперечного импульса частиц.

Тем не менее, статистическая модель удовлетворительно описывает ряд характеристик взаимодействий — распределения по полной энергии вторичных частиц в системе центр масс, по эффективным массам систем частиц, в которых отсутствуют резонансы и рост средней множественности от энергии. Средняя множественность заряженных частиц по модели Ферми-Ландау имеет следующее соотношение

,

а модель Померанчука даёт

Фейнбергом показано, что зависимость от энергии для статистических подсистем

.

Кроме того, по предсказанию статистической модели, основную долю вторичных частиц составляют π-мезоны (80–90 %). При этом образование π-мезонов (π⁺, π^-, π⁰) происходит с равной вероятностью. Как показано Фейнбергом процессы генерации частиц при высоких энергиях могут быть частично описаны статистическими моделями.

Существующие модели для описания процессов множественного рождения построены на основе двух типов неупругих взаимодействий: дифракционных и периферических. Для пояснения рассмотрим процесс столкновения двух адронов а и b при высоких энергиях, когда в конечном состоянии рождается определенное число частиц определенного типа. По-видимому, при высоких энергиях основной вклад в этот канал дают те события, которые соответствуют обмену вакуумными квантовыми числами между группами образовавшихся частиц. Общая форма произвольного процесса имеет вид

Квантовые числа частиц а и b совпадаютсквантовыми числами групп частиц () и () соответственно. Причем инвариантная масса каждой из групп частиц конечна и слабо зависит от S при (S — полная энергия). Квантовые числа системы частиц () совпадают с вакуумными. Здесь частицы а_i и b_i являются продуктами дифракции а и b соответственно, а частицы с_i продуктами пионизации.

Из дифракционной модели следует, что полное сечение рассматриваемого процесса остаётся постоянным, а средняя множественность растет с энергией логарифмически. Действительно, сечение при больших множественностях выражается соотношением (). Средняя множественность в таком случае (при и ) имеет вид

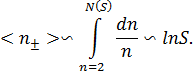
(где ).

Теперь перейдем к рассмотрению некоторых свойств мультипериферической модели. Мультипериферическая модель впервые была рассмотрена Амати, Фубини, Стангеллини и Тонини (AFST — модель, см. рис. 1).

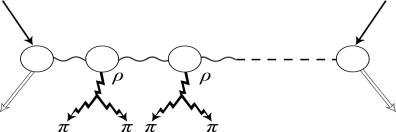
Рис. 1. Фейнмановская диаграмма модели AFST (мультипериферическая модель) полностью периферического взаимодействия

Многие экспериментальные и теоретические работы утверждают, что существенный вклад в полное сечение взаимодействия адронов при высоких энергиях дают процессы мультипериферического типа. Характерная особенность этих процессов состоит в том, что все рожденные частицы имеют малые поперечные импульсы, а их продольные импульсы упорядочены, так что импульс каждой следующей частицы меньше чем импульс предыдущей. При этом полные энергии соседних адронов ² и квадраты переданных импульсов невелики (не растут с ростом полной энергии). Если ограничиться только такими процессами, то можно вычислить сечение рассеяния адронов при высоких энергиях. Мультипериферические процессы объясняют многие качественные и количественные стороны сильных взаимодействий (при ): постоянное полное сечение, логарифмический рост множественности при возрастании энергии, масштабную инвариантность для инклюзивных реакций и факторизацию.

Логарифмический рост множественности является наиболее характерным предсказанием мультипериферических моделей и основным отличием их от моделей статистического типа.

В настоящее время для сравнения с экспериментальными результатами для неупругих процессов при высоких энергиях часто пользуются другим вариантом мультипериферической модели, предложенной Чаном, Лоскиевичем и Аллисоном (CLA — модель).

В CLA модели амплитуда представляется в виде суммы парциальных периферических диаграмм. Амплитуды для отдельной диаграммы записывается

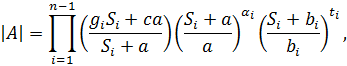
где п — число частиц в канале: , , и — параметры (универсальные константы); — точка пересечения i-й траектории Редже с осью t = 0; — квадрат переданного 4-импульса от падающей частицы к i-й; — квадрат инвариантной энергии частиц i и i+1 за вычетом квадрата суммы их масс покоя. Возможные для рассматриваемой топологии событий диаграммы получаются с учетом всех перестановок вторичных частиц, соответствующих обмену квантовыми числами известных частиц.

Модель удовлетворительно описывает такие характеристики взаимодействий как угловые распределения барионов и мезонов в системе центра масс, распределение вторичных частиц по продольному и поперечному импульсу и зависимость среднего поперечного импульса от продольного. Однако при низких множественностях наблюдается расхождение предсказаний модели с экспериментом. Это расхождение обусловлено, вероятно, влиянием образования резонансов, не учитываемого в данной модели. В дальнейшем развитии модели были предприняты попытки включить образование резонансов. В этом случае в узлах диаграммы образуются двухпионные резонансы (бозоны). Предсказания CLA — модели, полученные после этого, лучше согласуются с экспериментом. Однако в этом случае необходимо вводить в модель для каждой реакции эмпирические параметры (вероятности рождения резонансов), что существенно снижает общность модели.

По мультипериферической модели зависимость множественности вторичных заряженных частиц от энергии имеет вид [3].

Многие теоретические модели приводят к пуассоновскому или дираковскому распределению генерированных частиц [4].

Литература:

1. Абдурахимов А. У., Зайнабидинов С. З., Курбанов А. О., Мадаминов Х. М. Множественные процессы и масштабная инвариантность // Материалы VIII Конференции «РНПК». — Ташкент:, 2015. — С. 26–28.
2. Ландау Л. Д. // Известия АН СССР. — 1953. — № 17. — С. 51.
3. Абдурахимов А. У., Мадаминов Х. М., Зиёитдинов Ж. Н. Исследование средней множественности заряженных частиц адрон-адронных взаимодействиях при высоких энергиях (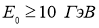).// Материалы IX Конференции «РНПК». — Ташкент:, 2016. — С. 232–234.
4. Абдурахимов А. У., Мадаминов Х. М., Зиёитдинов Ж. Н. Электрон и дельта-функция Дирака // Молодой ученый. — 2017. — № 1. — С. 1–4.