Обзор моделей распространения информации в социальных сетях



Обзор моделей распространения информации в социальных сетях

Горковенко Дмитрий Константинович, аспирант

Байкальский государственный университет

Введение

Анализ социальных сетей используется в целях маркетинга, бизнес-аналитики для улучшения процессов взаимодействия с клиентами. Инструменты анализа позволяют оценить индивидуальные и групповые предпочтения клиентов, выявить тренды интересов и в дальнейшем решать важные стратегические задачи фирмы.

В настоящее время социальные сети играют фундаментальную роль в распространении информации [1-4]. Рассмотрим два основных способа получения информации. Информация может поступить через связи в социальных сетях, либо через средства массовой информации (далее – СМИ). Оценка эффекта от распространения информации через СМИ была сложной задачей. Однако, с появлением веб-блогов и других сетевых медиа (новостные порталы, форумы и пр.), анализировать распространение информации стало проще. Вся информация хранится в сети в открытом доступе, пользователи открыто делятся своими мнениями по поводу информации как в текстовом виде, так и через рейтинговые системы (например, отметки «мне нравится», «поделится»). Это все позволяет более точно изучать процессы диффузии информации, оценивать эффект от распространения. Однако, моделирование диффузии в социальных сетях остается сложной задачей. Довольно сложно получить большое количество разнообразной информации из разных источников, обработать и отследить элементы социальных сетей такие как: рекомендации, ссылки, теги, сообщения, фразы и «мемы» [3].

Процесс распространения удобно поделить на две части: непосредственно распространение информации и изменение мнений агентов сети о информации. Существуют различные работы, посвященные изучению как распространению информации [5-7], так и изучению изменения мнений в социальной сети [6, 9-16]. Процесс распространения информации в социальной сети через узлы связей похож на эпидемию [17, 18]. Скорости распространения информации очень высоки (при условии, что информация новая и вызывает интерес), распространение начинается с малых групп и переходит на все большие группы, пока не достигнет пика и не пойдет на спад.

Распространение информации в социальных сетях

Модель SIR

Детерминированная модель эпидемии SIR (susceptible – infected- removed) описывает способ передачи эпидемии от одного индивида (агента) к другому. Процесс Имеет параметр затухания [7]. Состояние агента можно описать тремя типами: уязвимое, зараженное, невосприимчивое.

Количество агентов в сети можно выразить как , где – количество уязвимых агентов, – количество зараженных агентов, – количество невосприимчивых агентов. Невосприимчивое состояние можно интерпретировать как потеря интереса к новости и дальнейшее нежелание распространять её. В модели используются следующие параметры:

— средняя частота заражения;

— постоянная средняя скорость «выздоровления» в единицу времени;

Модель можно представить в виде системы уравнений:

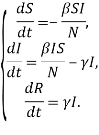
Расширенная модель SIR

Социальная сеть обладает изменчивостью во времени – это означает, что агенты могут присоединиться к сети или покинуть сеть. Обозначим параметром среднюю частоту присоединения к сети в единицу времени. Параметром будем считать среднюю частоту выхода агента из сети в единицу времени. Система уравнений примет следующий вид:

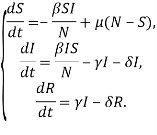
Вероятность перехода из невосприимчивого состояния в уязвимое введем параметр . Добавим данное условие в систему уравнений модели:

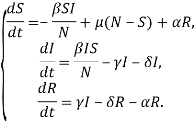
Модель Далея-Кендалла

Известен метод Далея-Кендалла описанный в 1965 году [6] – математическая модель имитации процесса распространения информации (слухов), так же называется DK модель. Данная модель делит население на три разные группы:

— группа, которая начинает распространение слуха ();

— группа, которая после получения слуха продолжает распространять его ();

— группа, которая после получения слуха принимает решение не распространять его ().

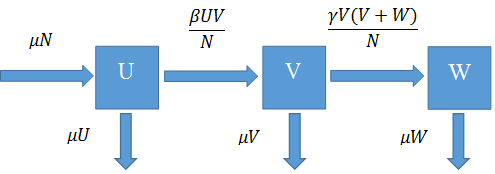
Рисунок 1. DK модель распространения слухов.

Модель, представлена на рисунке 1. число участников процесса распространения. Слух распространяется с вероятностью . Степень принятия слуха определена параметром . Когда распространитель слухов сталкивается с аудиторией , то растространение прекращается и вероятность что это произойдет равна . Слух теряет свою ценность с течением времени. Такая вероятность определяется фактором . Это можно объяснить тем, что слух перестает быть новинкой или не остается частей, которые можно передать. Модель можно представить в виде уравнений:

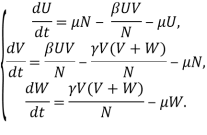
Решение системы можно представить в виде [20]:

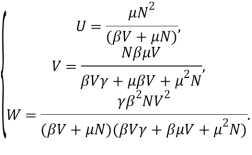
Определим и , запишем решение системы в виде:

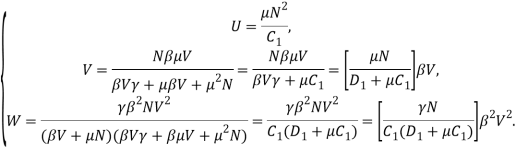
Клеточный автомат

Клеточный автомат — это дискретная динамическая система, включающая однородные клетки соединенные друг с другом. Все клетки образуют клеточный автомат [19]. Состояние каждой клетки определяется клетками, находящимися в окрестности данной клетки. Набор «ближайших соседей» называется окрестностью конечного автомата с номером . Состояние клеточного автомата в момент времени определяется следующим образом:

где правило, которое может быть выражено (например в язык булевой алгебры), соседи, шаг. Клеточный автомат определен правилами:

— изменение значений каждой клетки происходит одновременно (шагом является изменение единицы времени);

— сеть клеточного автомата является однородной, т.е. правила изменения состояния одинаковы для всех ячеек;

— клетка может влиять, только на клетки соседей;

— число состояний клетки конечно.

Теория клеточных автоматов используется для анализа диффузии инноваций, этот процесс очень похож на распространение новостей в интернете. Простейшая функция преобразования модели отвечает следующим правилам: индивидуум соответствует одной клетке, которая может принимать два состояния: 1 – новость принята, 0 – новость не принята. Предполагается что, однажды приняв информацию, состояние остается неизмененным. Автомат принимает решение о принятии новости ориентируясь на мнение ближайших соседей, если среди соседей поддержали инновацию и вероятность принятия новости (генерируется в ходе работы модели), тогда если где фиксированное пороговое значение, клетка принимает инновацию. Кроме того, могут быть наложены дополнительные условие на тип новости: клетка располагает свежими новостями (черный цвет), у клетки находится устаревшая информация (серый цвет), клетка не располагает информацией или забыла о ней (белый цвет).

Правила распространения новости:

— в начале каждая клетка закрашена белым цветом, кроме одной черной клетки (которая получила новость);

— белая клетка может изменить цвет на черный или остаться белой (это означает приняла новость или осталась в неведении);

— белая клетка меняет свой цвет, если условие выполняется в модели распространения диффузий(число черных клеток, если , то увеличивается в раза);

— если ячейка черная и все ячейки вокруг только черные или серые, она меняет свой цвет на серый (новость устаревает);

— если ячейка серая и ячейки вокруг только черные или серые, то она меняет свой цвет на белый (информация забыта).

Изменение мнений агентов

Кроме распространения информации в сети интересно рассмотреть процесс формирования и динамики мнений в социальной сети. После получения какого-либо сообщения агент социальной сети формирует мнение о нем. Рассмотрим известные модели влияния в социальных сетях.

Модели с порогами

Агент может находится в активном и неактивном состояниях, причем возможен переход только из неактивного состояния в активное (обратный переход не допускается). Если агент испытывает влияние каждого своего -го соседа в сети так, что выполняется условие , и становится активным в зависимости от выбранного им порога (значение может быть фиксированным для всех агентов [15] или может быть выбрано случайным образом в соответствии с некоторым вероятностным распределением[16]), то условие активации: [14].

Модель независимых каскадов

Данная модель принадлежит к моделям систем взаимодействующих частиц. Состояние агента определяется аналогично узлу в модели с порогами. Если агент становится активным, то на следующем шаге (строго на следующем) он может активировать соседей с вероятностью [17].

Модель сетевой автокорреляции

В работе [20] модель изменения мнений представлена в виде детерминированной системы. Мнения агентов представлены в виде вектора действительных чисел . Изменение мнений агентов во времени описаны уравнением , где – матрица влияний, – величина влияния агента на агента .

Модель адаптивно-подражательного поведения (МАПП)

МАПП рассматривается в работе [21] и описана в рамках теории игр как , где – множество стратегий участников игры, – распределение игроков по стратегиям, – выигрыш игроков, использующих стратегию . На каждом шаге агент с индексом с некоторой интенсивностью переходит в адаптивное состояние, при котором он пересматривает свое мнение (стратегию). В адаптивном состоянии агент меняет свое мнение на мнение агента в соответствии с вероятностью . Далее сравнивается альтернативная и текущая стратегия. Если выбранная для сравнения стратегия лучше исходной (дает агенту больший выигрыш), то с вероятностью игрок меняет свое мнение.

Марковская модель влияния

При исследовании социальных явлений многие исследователи используют марковские цепи [13, 14]. В работе [8] описано применение марковских цепей для изучения динамики влияний в социальных сетях. Динамику влияний опишем марковским процессом, а мнения будем рассчитывать при помощи матрицы влияний. Рассмотрим данную модель более подробно.

Введем в работу нашего автомата дополнительный шаг: изменение мнений. Агенты в сети влияют друг на друга и степень влияния зададим в виде квадратной матрицы размерности , где обозначается степень доверия -го агента -му агенту. Обозначим понятия влияние и доверия, будем считать что эти два понятия являются противоположными в следующем смысле: выражение «степень доверия -го агента -му равна » тождественно по смыслу выражению «степень влияния -го агента на -го равна » [21]. Будем считать, что агент достоверное знает только «свою» строку матрицы кому и насколько он доверяет. Так же введем условие нормировки для матрицы :

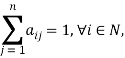
т.е. предположим, что «суммарное доверие» агента равно единице. Это условие означает, что матрица является стохастической по строкам. Агент может доверять самому себе, т.е.

Если -й агент доверяет -му, а -й доверяет , то это означает следующее: -й агент косвенно влияет на -го (хотя -й агент может не знать о его существовании). Все это определяет формирования мнений членов социальной сети.

В момент времени у каждого агента есть мнение по некоторому вопросу, положим что мнение -го агента отражает вещественное число . Мнения всех агентов сети в момент времени отражает вектор столбец мнений размерности . Агенты в социальной сети взаимодействуют, обмениваясь мнениями. В следующий момент времени мнение каждого агента зависит от мнений агентов, которым он доверяет. Будем считать изменение мнений линейным, .т.е. мнение агента является взвешенной суммой мнений агентов, которым он доверяет (весами являются доверия ):

В векторной записи изменение мнений агентов можно записать в виде . При условии, что число агентов в сети не изменяется (как и их матрица влияния), то можно записать и т.д. При достаточно долгом взаимодействии мнения агентов будут стремится к их результирующему значению .

Имея уравнение изменения мнений агентов (выражение (1)), можно решать задачу управления — воздействия на агентов социальной сети с целью формирования определённых мнений. Есть некоторый управляющий орган, которому известна матрица влияний. Воздействие заключается в изменении вектора начальных мнений. Введем вектор управления , воздействие на шаге можно записать в виде .

Пусть имеется целевая функция — критерий эффективности управления — зависит от итоговых мнений агентов и вектора управления. Задачу управления можно записать в виде:

Задача будет сведена к выбору агентов, на которых имеет смысл воздействовать и выборе меры воздействия на конкретного агента.

Заключение

Данная статья посвящена методам моделирования распространения информации в социальных сетях и изучению изменения мнений посредством информационного управления. Планируется использовать данные, полученные с помощью алгоритмов генерации социальных сетей. Такие алгоритмы позволяют задать различные варианты социальных сетей, проверить модели на разных условиях для исследования ситуаций, в которых модель лучше всего будет адаптирована. Описано применение клеточных автоматов для моделирования процесса распространения информации в социальных сетях. Благодаря применению марковских цепей для описания процесса изменения мнений существует возможность решать задачу информационного влияния в социальных сетях. Что необходимо для оптимального выбора агентов, на которых нужно оказывать влияние для достижения необходимого результата.

В дальнейшем планируется, после тестирования моделей на сгенерированных данных, апробация модели на реальных данных, полученных из социальных сетей. Это позволит внести корректировки в модели для дальнейшего анализа и использования моделей на практике. Построенные и апробированные модели будут сформированы в виде программного пакета для анализа распространения информации в социальных сетях и оценки информационного влияния.

Литература:

1. M. Cha, H. Haddadi, F. Benevenuto, and K. P. Gummadi. Measuring User Influence in Twitter: The Million Follower Fallacy. In ICWSM ’10 , 2010.
2. M. Goetz, J. Leskovec, M. Mcglohon, and C. Faloutsos. Modeling blog dynamics. In ICWSM, 2009.
3. J. Leskovec, L. Backstrom, and J. Kleinberg. Meme-tracking and the dynamics of the news cycle. In KDD ’09, 2009.
4. D. Liben-Nowell and J. Kleinberg. Tracing information flow on a global scale using Internet chain-letter data. PNAS, 105(12):4633–4638, 2008.
5. Носова М. В., Сенникова Л. И. Моделирование распространения информации в децентрализованных сетевых системах с нерегулярной структурой // Новые информационные технологии в автоматизированных системах. 2014. №17.
6. Daley DJ, Kendall DG, Stochastic rumors, J. Inst. Math. Appl. 142(1965), pp. 42-55.
7. Kermack, W. O.; McKendrick, A. G. (1927). "A Contribution to the Mathematical Theory of Epidemics". Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences. 115 (772): 700. Bibcode:1927RSPSA.115..700K. doi:10.1098/rspa.1927.0118. JSTOR 94815.
8. Губанов Д.А., Новиков Д.А., Чхартишвили А.Г. «Социальные сети: модели информационного влияния, управления и противоборства», 2010 – 228 стр.
9. Granovetter M. Threshold Models of Collective Behavior // American Journal of Sociology. 1978. V. 83, № 6. P. 1420-1443.
10. Kempe D., Kleinberg J., Tardos E. Maximizing the Spread of Influence through a Social Network / Proceedings of the 9-th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. 2003. P. 137 – 146.
11. Myerson R.B. Game Theory: Analysis of Conflict. — London: Harvard Univ. Press, 1991.
12. Goldenberg J., Libai B., Muller E, Talk of the Network: A Complex Systems Look at the Underlying Process of Word-of-Mouth // Marketing Letters. 2001 № 2. P. 11-34.
13. De Groot M.H. Reaching a Consensus // Journal of American Statistical Assotiation. 1974. № 69. P. 118-121.
14. Робертс Ф.С. Дискретные математические модели с приложениями к социальным, биологическим и экологическим задачам. — М.: Наука, 1986.
15. Friedkin N.E. Structural Cohesion and Equivalence Explanations of Social Homogeneity // Sociological Methods and Research. 1984. № 12. P. 235-261.
16. Васин А.А., Краснощеков П.С., Морозов В.В. Исследование операций. — М.: Издательство Академия, 2008.
17. H. W. Hethcote. The mathematics of infectious diseases. SIAM Review, 42(4):599–653, 2000.
18. Башабшех Мурад Махмуд, Масленников Борис Иванович, Скворцов Андрей Викторович Комбинированная имитационная модель пространственного распространения эпидемических заболеваний по холере на основе вероятностного клеточного автомата // Интернет-журнал Науковедение. 2013. №3 (16).
19. John Von Neumann, John; Burks, Arthur W. (1966), Theory of Self-Reproducing Automata. University of Illinois Press, Urbana and London 1966.
20. R. Isea and R. Mayo-García. Mathematical analysis of the spreading of a rumor among different subgroups of spreaders. Pure and Applied Mathematics Letters (2015), Vol. 2015, pp 50-54.
21. Губанов Д.А. Обзор онлайновых систем репутации/доверия. Интернет конференция по проблемам управления. М.: ИПУ РАН, 2009. 25с.