Приведена методика расчета формирования ветровых волн на водотоках (проточные водохранилища, крупные и малые реки, большие каналы) с учетом встречных и попутных течений и ограниченностью разгона берегами.
Ключевые слова: формирования ветровых волн, встречные и попутные течение, сохранения волнового действия, спектральная плотность, время распространения волн
There is given a technique of procedure of the formation of wind waves on streams (flow-through reservoirs, large and small rivers, large channels), taking into account oncoming and passing currents and limited dispersal banks.
Keywords: the formation of wind waves, counter-current, wave action conservation, spectral density, time of wave propagation
Факторами, определяющими генерацию ветровых волн на крупных водотоках (проточные водохранилища, крупные реки, большие каналы) по сравнению с открытым морем, являются течение и ограниченность разгона берегами. Совместное действие обоих факторов изучалось в [1, 2, 3, 4, 6, 7, 8, 10]. Сделаем краткий обзор соответствующей теории, положенной в основу методики расчета формирования ветровых волн на водотоках.
Для ветровых волн на крупномасштабном течении основным динамическим уравнением является уравнение сохранения волнового действия, которое применительно к рассматриваемой задаче можно записать в виде:
![]() ,(1)
,(1)
где:
![]() (2)
(2)
спектральная плотность волнового действия, ![]() - пространственный амплитудный спектр волн, r — частота, соответствующая спектральной компоненте
- пространственный амплитудный спектр волн, r — частота, соответствующая спектральной компоненте ![]() в точке
в точке ![]() в момент времени t в системе отсчета, движущейся со скоростью течения
в момент времени t в системе отсчета, движущейся со скоростью течения ![]() . Принцип сохранения волнового действия справедлив для волн в движущейся среде, был установлен Bretherton, Garret в 1969 г. [9] и развит для волн на воде Уиземом.
. Принцип сохранения волнового действия справедлив для волн в движущейся среде, был установлен Bretherton, Garret в 1969 г. [9] и развит для волн на воде Уиземом.
В одномерном случае уравнение (1.1) упрощается следующим образом:
![]() .(3)
.(3)
Характеристики уравнения (3):
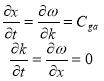 ,(4)
,(4)
где Cga — абсолютная групповая скорость, Cga=Cgr+U. В соответствии с (3) и (4) условие на характеристиках имеет вид:
![]() .(5)
.(5)
В установившемся режиме, при достижении достаточного времени волновое действие перестает зависеть от времени, а является только функцией разбега. При этом, уравнение (1.5) принимает совсем простой вид:
![]() .(6)
.(6)
Следовательно, используя метод характеристик и разделяя в уравнении (1.6) переменные, можно решение уравнения (3) записать в следующем неявном виде:
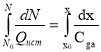 ,(7)
,(7)
где
![]() (8)
(8)
является граничным условием. Так как групповая скорость при постоянных глубине и скорости течения не зависит от координаты, то правая часть уравнения (7) приводится к виду:
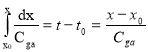 ,(9)
,(9)
где t-t0 — время распространения волн с групповой скоростью от граничного створа. Из (7) и (9) следует, что следующее преобразование координаты (при x0=0)
![]() (10)
(10)
где Cg0 — групповая скорость на неподвижной воде, дает на расстоянии разбега x на течении величину волнового действия N(x), равную N0(X) — величине волнового действия на длине разбега X на неподвижной воде. Таким образом, соотношение (10) определяет эффективную длину разгона для ветровых волн на течении.
Более подробно определение эффективной длины разгона для волн на течении рассмотрено в [6], где, в частности, показано, что если угол между векторами ветра и течения равен , то эффективная длина разгона определяется соотношением:
![]() , (11)
, (11)
где C gr — групповая скорость волн в системе координат, связанной с течением.
Понятие эффективной длины разгона для волн на течении дает правильную качественную тенденцию влияния течения на развитие волн. Действительно, на глубокой воде ![]() и на попутном течении (U>0) из (1.10) следует, что X/x<1, т. е. эффективная длина разгона меньше фактической. Наоборот, на встречном течении (U<0) из (10) следует, что X/x>1, т. е. эффективная длина разгона больше фактической, геометрической длины. Такой эффект течения соответствует данным, полученным в аэрогидродинамических каналах, где на попутном течении ветровые волны меньше, а на встречном течении больше, чем при отсутствии течения при прочих равных условиях.
и на попутном течении (U>0) из (1.10) следует, что X/x<1, т. е. эффективная длина разгона меньше фактической. Наоборот, на встречном течении (U<0) из (10) следует, что X/x>1, т. е. эффективная длина разгона больше фактической, геометрической длины. Такой эффект течения соответствует данным, полученным в аэрогидродинамических каналах, где на попутном течении ветровые волны меньше, а на встречном течении больше, чем при отсутствии течения при прочих равных условиях.
Эффективная длина разгона может быть определена из уравнения (11), в котором необходимо задать величину относительной групповой скорости. Для этого может быть использована экспериментальная зависимость для частоты максимума спектра волн в системе координат течения:
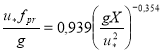 (12)
(12)
где u* — скорость трения ветра в неподвижной системе координат. Если перейти в соотношении (12) к скорости ветра и средней частоте в спектре с помощью следующих соотношений:
![]() ,(13)
,(13)
то выражение (12) принимает вид:
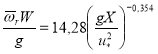 ,(14)
,(14)
где r — средняя относительная круговая частота. Тогда для средней групповой скорости получаем:
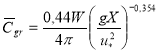 .(15)
.(15)
А для эффективной длины разгона из соотношения (11) получается следующее неявное уравнение:
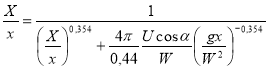 .(16)
.(16)
Численное решение уравнения (16) показано на рис.1. На рис.1а решение относится к попутному течению, когда ![]() и X/x<1. На рис.1б показано решение для встречного течения:
и X/x<1. На рис.1б показано решение для встречного течения: ![]() и X/x>1. Кривые на рис.1 наглядно демонстрируют, насколько может быть важен фактор течения, который может увеличивать или уменьшать длину разгона, особенно на ограниченных длинах разгона.
и X/x>1. Кривые на рис.1 наглядно демонстрируют, насколько может быть важен фактор течения, который может увеличивать или уменьшать длину разгона, особенно на ограниченных длинах разгона.
Введение эффективной длины разгона позволяет использовать для расчета средних высоты и периода волн на течении следующие формулы ГОИН-СоюзМорНИИпроекта [5]:
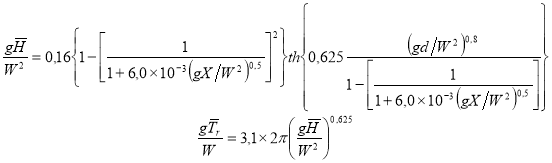 ,(17)
,(17)
где Tr — период волн в движущейся системе координат (в системе течения), d — глубина воды на разгоне. Как показано в [5], зависимости (17) согласуются для случая отсутствия течения с большим объемом данных натурных измерений волн.
При прогнозировании ветровых волн на ограниченных акваториях (крупные реки, каналы, водохранилища, береговая зона моря) необходимо учитывать ограничение разгона береговой линией. Этот фактор в условиях узостей или сложной конфигурации береговой линии может быть не менее важен, чем течение.
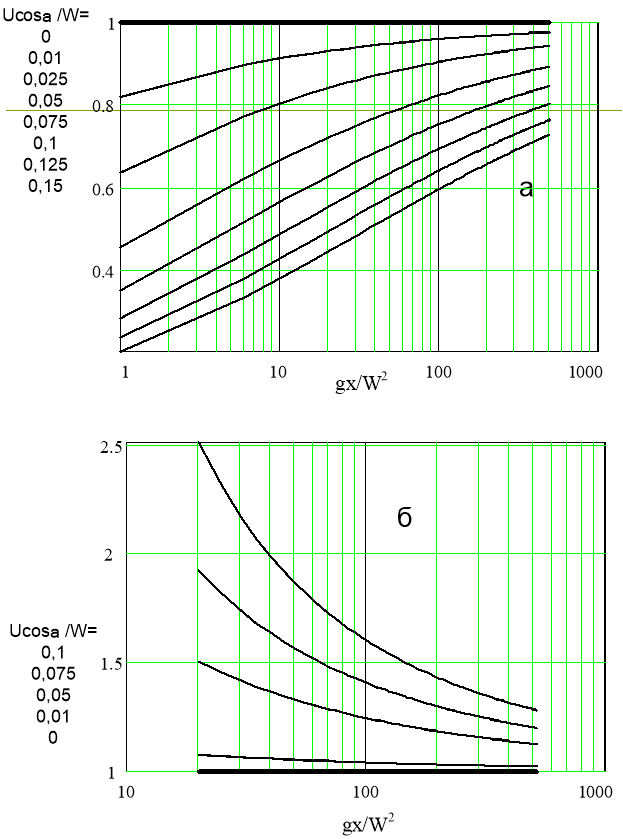
Рис. 1. Безразмерная длина разгона для ветровых волн на течении: а — на попутном течении, б — на встречном
Здесь также используется эффективная длина разгона, которую будем называть эффективной по ограничению разгона. Последняя величина определяется интегрированием длин разгона, измеренных от расчетной точки до пересечения с линией берега, по углу между локальным и генеральным направлениями скорости ветра:
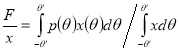 ,(18)
,(18)
где ’ — растр углов эффективного волнообразующего действия ветра, p() — весовая функция.
Растр эффективного волнообразования принимается равным 90 градусов в обе стороны от генерального направления для сложного очертания береговой линии и от 30 до 90 градусов в случае водотоков. Вид весовой функции зависит от распределения скорости ветра по направлениям и от местных условий. Так при ’=300 и p()=1 получается часто используемое для каналов решение:
![]() ,(19)
,(19)
где b — ширина канала. Вид функции (19) показан на рис.2.
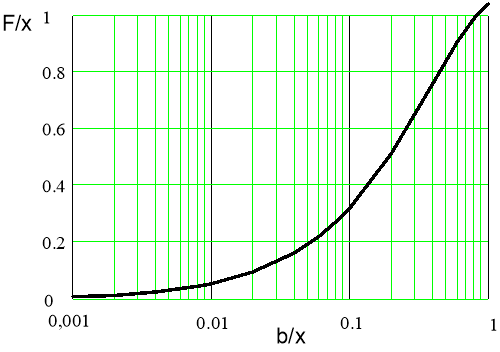
Рис. 2. Влияние относительной ширины русла на разгон волн
Методика расчета, учитывающая влияние как течения, так и сложной конфигурации береговой черты, состоит в следующем и используется далее для расчета размеров ветровых волн в районе исследуемого перехода. Принципы методики подробно изложены в работах [7,8].
Алгоритм представляет обобщение метода расчета ветровых волн при сложной конфигурации береговой черты. Из расчетной точки с интервалом 22,5 градуса в обе стороны от главного луча с номером n=1 проводят дополнительные лучи с номерами ![]() . Затем по каждому лучу определяется эффективная длина разгона по течению:
. Затем по каждому лучу определяется эффективная длина разгона по течению:
![]() ,(20)
,(20)
где — длина расчетного участка, (X/x)i определяется по формуле (16), в которой участвует соответствующая проекция скорости течения. Луч продолжается до пересечения с линией берега. В случае относительно небольших разгонов можно пренебречь искривлением волнового луча и использовать соотношение (20) для луча целиком.
Далее, для каждого волнового луча по первой формуле (1.17) вычисляется средняя высота волн, средняя высота волн для исследуемой акватории определяется взвешенным осреднением в соответствии с рекомендациями [13]:
![]() .(21)
.(21)
Затем по второй из формул (17) определяется средний период волн.
Для перехода от средних высоты и периода волн к высоте и периоду заданной обеспеченности в системе используется функция распределения высот ветровых волн в форме распределения Рэлея, которая предполагается справедливой и для эффективного разгона. В частности, для определения высоты и периода значительных волн можно применить соотношения:
![]() .(22)
.(22)
Как показывают измерения, для встречного течения существует особенность, относящаяся к начальному участку разгона. На этом участке формируемые ветровые волны распространяются вниз по течению, а по ветру, т. е. вверх по течению распространяются группы волн. Естественно предположить, что для данной волны длина начального участка определяется соотношением:
![]() ,(23)
,(23)
Что, используя выражение (15) для групповой скорости, можно записать в виде:
![]() .(24)
.(24)
Если решать для луча на встречном течении уравнения (24) и (16) совместно, то можно учесть эффект начального участка.
Разработанная методика подтверждена натурными измерениями, выполненными на Каракумском канале авторами, а также данными измерений САНИИРИ на нескольких среднеазиатских каналах [6]. Для представления о диапазонах выполненного сопоставления, данные измерений автора вместе с данными расчетов представлены в табл.1.1.
Таблица 1
Сравнение результатов расчета высот ветровых волн сданными измерений
|
Длина разгона, м |
Ширина канала, м |
Глубина воды, м |
Скорость ветра, м/с |
Скорость течения, м/с |
Средняя высота волн, см | |
|
Измерения |
Расчет | |||||
|
256 |
134 |
4,6 |
5,3 |
-0,42 |
4,5 |
4,3 |
|
258 |
134 |
4,6 |
6,9 |
-0,42 |
5,8 |
6,7 |
|
258 |
134 |
4,6 |
4,1 |
-0,42 |
3,3 |
3,0 |
|
795 |
167 |
3,8 |
5,7 |
0,42 |
6,0 |
6,1 |
|
795 |
167 |
3,8 |
5,8 |
0,42 |
6,3 |
6,2 |
|
137 |
55 |
3,2 |
9,4 |
-0,55 |
8,0 |
5,8 |
|
198 |
55 |
3,2 |
6,1 |
-0,55 |
5,6 |
3,7 |
|
180 |
50 |
2,1 |
15,8 |
-0,53 |
14,0 |
14,0 |
|
125 |
50 |
2,1 |
17,2 |
-0,53 |
13,0 |
11,0 |
|
180 |
50 |
2,1 |
6,0 |
-0,53 |
1,6 |
1,5 |
Из таблицы видно, что сравнение результатов расчета высот ветровых волн с данными измерений дают хорошее соотношение.
В заключении можно сделать следующий вывод, что при расчете образования ветровых волн на течении в проточных водохранилищах, крупных и малых реках, и больших каналах можно воспользоваться предлагаемой методикой расчета.
Литература:
- Атажанов А., Кантаржи И. Г., Сапова Н. О. Развитие метода прогноза ветровых волн на водотоках. Труды ВНИИ ВОДГЕО, М., ВОДГЕО, 1989, 40–45.
- Заиров Х. И.. Листровой П. П., Масумов Р. Р. Прогноз элементов ветровых волн в крупных каналах. Гидротехническое строительство, 12, 1986, 44–46.
- Кантаржи И. Г. Метод прогноза ветровых волн на водотоках. Тр. ВНИИ ВОДГЕО, М, ВОДГЕО, 1987, 60–68.
- Кантаржи И. Г., Дрейзис Ю. И., Чеботкевич В. О. Прогноз ветровых волн в крупных каналах и проточных водохранилищах. Гидротехника и мелиорация, 1987, 2, 24–27.
- Масс Е. И., Кантаржи И. Г. и др. Метод расчета ветровых волн в больших каналах. Водные ресурсы, 1988, 1, 60–67.
- Рекомендации по расчету ветровых волн и транспорта наносов в больших каналах. Авторы: Е. И. Масс, И. Г. Кантаржи и др., М., ЦНИИС, 1986, 63 стр.
- Рекомендации по гидравлическому расчету крупных каналов. Авторы: Н. А. Ржаницын, В. С. Алтунин, Т. Г. Войнич-Сяноженцкий, Е. И. Масс, В. К. Дебольский, И. Г. Кантаржи и др. ГКНТ СССР, Союзгипроводхоз, М., 1986, 153 стр.
- Bretherton F. P., Garret C. J. R. Wave trains in inhomogeneous moving media. Proc. Roy. Soc., 1969, A, 302, 529.
- Kato H., Tsuruya H., Doi T., Mijarari Y. Experimental study of wind waves generated on water currents. 2nd report, Rep. Port Harbor Res. Inst. 1976, 15(4), 3–46.
- Kato H., Tsuruya H., Terakawa H. Experimental study of wind waves generated on water currents. 3rd report. Wave forecasting methods and its experimental confirmation. Rep. Port Harbor Res. Inst. 1981, 20(3), 94–129.

