Специфика многих современных задач биологии и медицины требует знания генома живых организмов, состоящего из нуклеотидных последовательностей дезоксирибонуклеиновой кислоты (ДНК).
На сегодняшний день существуют и применяются сборщики ДНК, собравшие уже множество известных геномов. Однако когда речь заходит о геномах большой длинны, осложненных значительным количеством повторяющихся участков, то гарантировать однозначную сборку генома становится невозможно. Также большинство сборщиков запрограммированы на работу с входными данными, полученными из строго определённых типов секвенаторов. Такой подход сокращает возможную область применения сборщиков и не удовлетворяет идеологии свободнораспространяемого ПО.
В данной работе представлено описание сборщика лишенного вышеперечисленных недостатков и показан пример его работы.
Описание алгоритма
Как и большинство современных сборщиков, предлагаемый подход использует парные чтения, получаемые из секвенаторов нового поколения, и в связи с этим работает на основе алгоритма использующего граф де Брёйна.
Разделим работу сборщика на следующие этапы:
- Нумерация чтений — каждое чтение получает уникальный идентификационный номер, позволяющий однозначно восстановить нуклеотидную последовательность в пределах одного чтения во время обхода графа.
- Построение графа де Брёйна и выбор числа k — любой граф может иметь вершины и рёбра. В нашем случае вершинами являются k — меры. Ребро из вершины 1 в вершину 2 проводится только тогда, когда суффикс длинны k — 1 из k — мера представляющего вершину 1, равняется префиксу k — мера вершины 2, т. е. ребро, по сути, является (k + 1) — мером.
- Упрощение графа. Если в графе находится путь, у которого входящие и исходящие степени всех внутренних вершин равны 1, то такой путь заменяется ребром.
-
Нахождение перспективных вершин. Для нахождения перспективных k — меров будем полагать, что вероятность нахождения вершины в исходном геноме тем выше, чем большее количество исходящих ребер она имеет. Обозначим
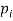 как количество всех исходящих ребер для вершины
как количество всех исходящих ребер для вершины 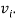 Тогда общее число всех исходящих ребер:
Тогда общее число всех исходящих ребер: 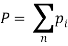 , где n — общее количество всех вершин. Найдем среднее значение исходящих ребер N для всего графа.
, где n — общее количество всех вершин. Найдем среднее значение исходящих ребер N для всего графа. 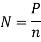 . Перспективными будем называть вершины имеющие значение исходящих вершин больше N. Количество перспективных вершин может варьироваться в разных библиотеках чтений от 5 % до 10 %.
. Перспективными будем называть вершины имеющие значение исходящих вершин больше N. Количество перспективных вершин может варьироваться в разных библиотеках чтений от 5 % до 10 %.
- Построение контигов. Для построения контигов используются начальные вершины обхода, хранящиеся в массиве перспективных вершин.
Реализация ирезультаты
Предложенный алгоритм был реализован на языке программирования Python и был протестирован на синтетической библиотеке чтений. Для хранения графа де Брёйна использовалась хэш-таблица, где ключом является k — мер (вершина графа), а значением исходящие рёбра и идентификационные номера чтений из которых были получены эти рёбра.
Синтетический геном имеет длину порядка 100000 нуклеотидов, средний размер чтений составляет 50 нуклеотидов, число чтений 13168. В эксперименте был проведен анализ качества контигов в зависимости от значения параметра k. Для этого для всех k множества {16, 20,26} была запущенна сборка.
В каждом случае было определено и записано качество картирования, насколько хорошо контиги картировались на референсный геном: считалась доля числа контигов, в которых доля правильных нуклеотидов была больше заданного порога. Результаты приведены в таблице 1.
Таблица 1
Результаты эксперимента по сборке синтетического генома для разных значений k
|
Длинна k— мера |
Качество картирования,% |
|
16 |
70 % |
|
20 |
81 % |
|
26 |
97 % |
По итогам проверки качества сборки было выбрано значение k = 26.
После получения графа де Брейна встала необходимость произвести сжатие элементарных путей. Был применен алгоритм сжатия, который позволил удалить около 20000 вершин из 111277. В результате получился граф готовый к построению контигов за приемлемое время. Характеристики полученных контигов представлены в таблице 2.
Таблица 2
Характеристики контигов для оптимального значения k— мера
|
Длина k-мера |
Количество контигов |
Максимальная длина контига |
Минимальная длина контига |
Средняя длина контига |
|
26 |
12809 |
11454 |
1602 |
6398 |
Время работы сборщика составило 452 минуты, из которых 22 минут заняло построение графа, 2 минут построение сжатого графа, и 428 минут сборка контигов. Необходимо отметить, что предложенный алгоритм является только частью процесса сборки геномной последовательности и полученные фрагменты нуждаются в дальнейшей обработке.
Заключение
В результате работы был разработан прототип сборщика, основанный на графе де Брёйна, который в перспективе позволит справиться с проблемой повторов в больших геномах. В будущем планируется, во-первых — переписать сборщик на более быстрый язык, например C++, во-вторых — использовать в его работе технологию параллельных вычислений CUDA.
Литература:
- Illumina [Электронный ресурс]: официальный сайт компании // Режим доступа: http://www.illumina.com/.
- Butler, J. Allpaths: de Novo assembly of whole-genome shotgun microreads / J. Butler. — Genome Research, 2008. — 496p.
- Daniel, R. Velvet: Algorithms for de Novo short read assembly using de bruijn graphs. Genome Research / R. Daniel. — Lecture Notes Comput., 2008. — 554p.

