Математическое моделирование структуры полимерных смесей на основе каучук-термопласт



Целенаправленное изменение значений потребительских и технологических свойств можно обеспечить изменением фазовой структуры полимерной композиции. Потенциальные возможности отдельных полимеров по расширению значений эксплуатационных свойств давно исчерпаны. Удовлетворение постоянно возрастающих требований потребителей по расширению областей использования и замене традиционных материалов металлов, дерева привело к созданию многокомпонентных смесей и сплавов. В случае научно обоснованного выбора отдельных компонентов, технологии и режимов переработки имеется возможность формирования фазовой структуры композиции, сочетающей наилучший набор необходимых значений полезных свойств.

Современные теории смешения основаны на идеализированном подходе к строению смесей. Моделируя один из компонентов в виде сферы и предполагая отсутствие межфазного слоя, структуру композиции каучук- термопласт можно представить в виде идеализированного агрегата. Размеры частиц компонента и его концентрация в композиции определяют размеры элементарной ячейки, габариты которой можно оценить по моделям куба или тетраэдра [1, 2].

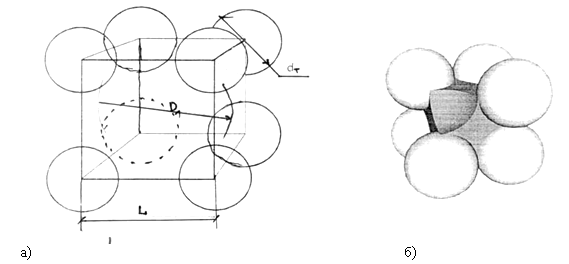
Рис. 1. Кубическая модель структуры смеси: а) схематическое изображение; б) объёмное изображение (без верхнего левого шара)

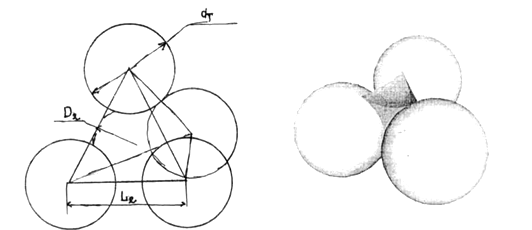
Рис. 2. Тетраэдрическая модель структуры смеси: а) схематическое изображение; б) объёмное изображение (без верхнего шара)

На рисунках 1, 2 схематично и объёмно изображены идеализированные модели композиции каучук — термопласт.

Массовая концентрация компонентов С_М, подсчитывается по формуле:

С_мт= (1)

где G — масса компонентов, индексы «т« и «к« соответствуют термопласту и каучуку.

При известных плотностях компонентов — ρ_т и ρ_к, можно рассчитать объёмную концентрацию компонентов С_о:

(2)

С_оm = 1 — С_ок(3)

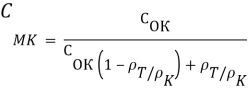(4)

Размер гранул термопласта и его концентрация в композиции определяют размеры элементарной ячейки, габариты которой можно оценить по предлагаемым моделям куба или тетраэдра.

Для менее плотного расположения частиц, описываемого моделью куба, при размерах гранул термопласта d_т, величина элементарной ячейки L₁ определяется уравнением

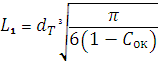(5)

Аппроксимируя форму частицы каучука в рассматриваемом агрегате в виде сферы, можно рассчитать её максимальный диаметр D₁, определяемый как расстояние между поверхностями сфер двух частиц термопласта, расположенных по диагоналям куба (рисунок 4):

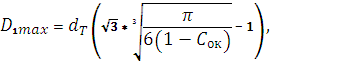(6)

где С_{ок —} объёмная концентрация каучука в диапазоне ;

— предельная концентрация каучука, при которой происходит касание гранул термопласта, расположенных по углам кубической модели.

Из условия: L₁ = d_m можно найти величину :

(7)

При меньших концентрациях каучука наиболее вероятно расположение частиц термопласта по углам тетраэдра. Для тетраэдрического расположения частиц термопласта (рисунок 2) размер ячейки L₂ определяется как:

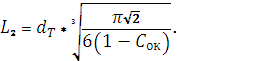(8)

Максимальный размер сферы каучука расположенный между сферами термопласта определяется следующей зависимостью:

(9)

где, С_ок — объёмная концентрация каучука в диапазоне ;

предельная объёмная концентрация каучука в агрегате, которой происходит касание гранул термопласта, расположенных по углам тетраэдра.

Из условия: L₂ = d_t определяется :

(10)

При таком соотношении компонентов структура материала представляет собой соприкасающиеся друг с другом, упакованные в виде тетраэдра, гранулы термопласта, а объём между ними заполнен частицами каучука.

При , рассчитанной для тетрагональной упаковки гранул термопласта, образование монолитной структуры возможно только за счёт деформации частиц полимера и уменьшения расстояний между центрами частиц, т. к. объёма каучука недостаточно, чтобы заполнить образовавшееся при этой упаковке пространство между частицами.

Исходя из приведённых расчётов, следует, что в зависимости от соотношения компонентов смеси, возможно, образование семи типов базовых структур. На рисунке (рисунок 3) представлены возможные структуры композиций во всём концентрационном диапазоне.

При объёмном содержании термопласта С_т= 1,000 создание монолитной массы возможно только при деформировании, и уменьшении расстояния между центрами сфер термопласта. При этом частицы термопласта теряют свою сферическую форму.

На концентрационном участке С_т > 0,662 — плотная тетраэдрическая упаковка гранул термопласта, пространство между гранулами заполнено частично воздухом, частично каучуком.

При С_т =0,662 — монолитная масса с плотной тетраэдрической упаковкой гранул термопласта с полностью заполненным пространством между гранулами каучуком.

В диапазоне содержания термопласта 0,662>С_т>0,523 — монолитная масса с рыхлой упаковкой гранул термопласта в виде тетраэдра и плотной кубической упаковкой, вокруг которых расположен каучук.

При С_т=0,523 — монолитная масса плотно кубически упакованных гранул термопласта в матрице каучука.

При Ст>0,523 — монолитная масса из рыхло упакованных гранул термопласта в кубическую решетку, расположенную в матрице каучука.

При С_т =0 — монолитная матрица каучука.

Таким образом, после завершения этапа загрузки и уплотнения композиция каучук-термопласт, в зависимости от соотношения компонентов, входит в стадию диспергирующего смешения в виде одной из указанных структур.

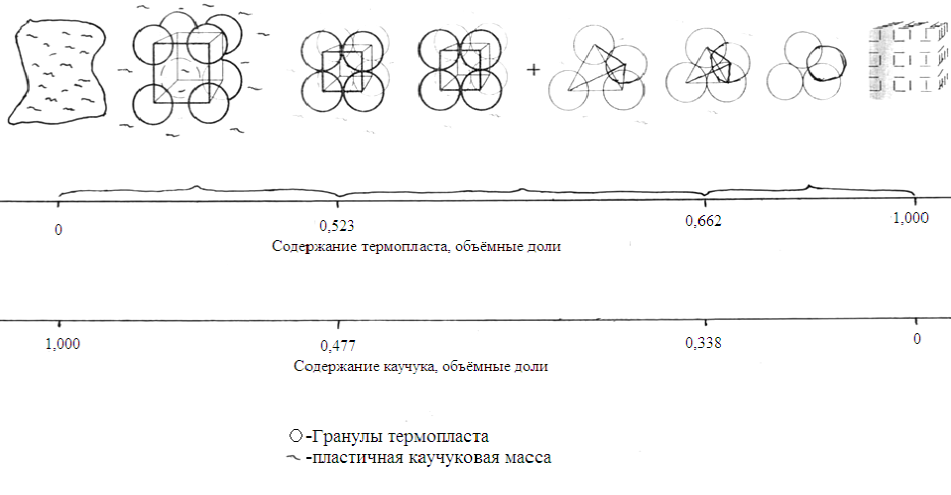
Рис. 3. Геометрическое моделирование фазовых структур смеси каучук-термопласт на всём концентрационном диапазоне

Приведённые геометрические модели не учитывают многие факторы, определяющие структуру двухкомпонентных систем, и могут быть использованы только для первичной оценки структуры композиции. Переход термопластов в расплав на втором этапе создания ТПР изменяет структуру композиции и на этом этапе процесса геометрические модели уже далеки от действительности.

Таким образом, становится очевидно, что изменение содержания компонентов приводит к изменению фазовой структуры композиции. Между размерами дисперсной фазы и дисперсионной среды существует прямая корреляция. Размеры частиц дисперсной фазы определяют размеры дисперсионной матрицы.

Литература:

1. Ким В. С. Исследования смешивающий способности экструзионных машин и разработка основ теории и методов расчёта- процессов смешения полимерных материалов в экструдерах. — М.: МИХМ, 1975. – 460 с.
2. Ахназарова С. Х. Методы оптимизации эксперимента в химический технологии. – М.: Высшая школа, 1985. – 327 с.