Самым дешевым и распространенным источником реактивной мощности в системах электроснабжения (СЭС), является управляемая батарея статических конденсаторов (БСК) [4, 5]. При включении и отключении БСК имеют место переходные процессы при коммутации емкостей.
Подключение БСК к СЭС сопровождается большими бросками тока по причине того, что незаряженная емкость при подключении к сети вызывает короткое замыкание согласно второму закону коммутации (напряжение на емкости не может измениться скачком) [1]. Ток в этот момент времени ограничен только сопротивлением сети, к которой подключается БСК [2]. В качестве доказательства рассмотрим следующую (простейшую) схему (рис.1), в которой возникает вышеописанный переходный процесс [3].

Рис. 1. Исследуемая схема
Пусть на вход схемы подано синусоидальное напряжение u(t), которое можно описать следующим уравнением:
u(t)=Umsinωt
После замыкания ключа (коммутация) имеем переходный процесс. Составим для этого случая уравнение по второму закону Кирхгофа:
u=uR+uc=iR+ uc
Согласно второму закону коммутации (напряжение на емкости скачком измениться не может) можно записать
uс(0-)= uc(0+)
Далее распишем напряжение на емкости uc(t) в виде суммы принужденной и свободной составляющих.
uC(t)= uспр(t)+uссв(t),
где uСсв(t)=Aept= Ae(-t/RC) — свободная составляющая.
С учетом последнего соотношения уравнение колебания напряжения на емкости запишем как
uc(t)= ucпр(t)+Ae(-t/RC)
Следующим этапом расчета будет нахождение принужденной составляющей напряжения, которая легко находится через принужденную составляющую тока.
Принужденную составляющую тока (в комплексном виде) можно найди следующим образом:
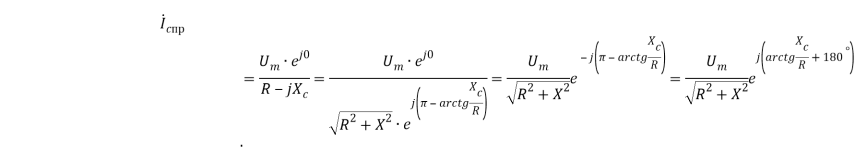
Тогда принужденная составляющая напряжения находится как произведение комплекса принужденной составляющей тока и комплексного емкостного сопротивления:
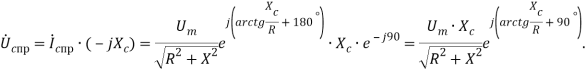
Теперь, когда мы знаем выражение для принужденной составляющей, мы можем найти и свободную составляющую напряжения в нулевой момент времени (при t=0+):
uc(0)= ucпр(0)+ucсв(0).
Подставляя uспр(0) в последнее выражение и, учитывая, что e0=1, получаем простейшее уравнение, из которого легко можно найти постоянную интегрирования А:
ucпр(0)+A=0,
откуда
A=- ucпр(0)=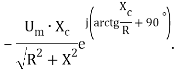
Окончательное выражение, описывающее колебания напряжения в режиме переходного процесса на емкости, равно:
uc(t)=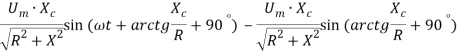 .
.
Для иллюстрации переходного процесса рассмотрим математическую модель, разработанную в программном комплексе «Matlab — Simulink».
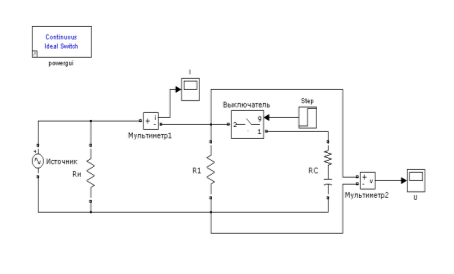
Рис. 2. Модель СЭС
Для получения более наглядной картинки переходного процесса внесем небольшое изменение в схему — параллельно источнику подключим активное сопротивление. Подобное изменение исходной схемы нам необходимо для того, чтобы увидеть изменение режима работы СЭС при подключении к ней БСК.
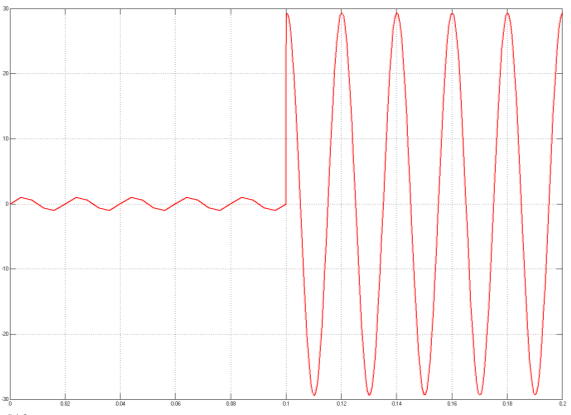
Рис. 3. Осциллограмма тока (осциллограф I)
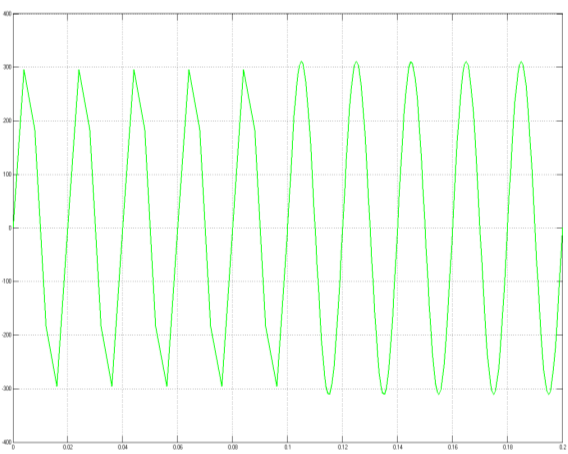
Рис. 4. Осциллограмма напряжения (осциллограф U)
Осциллограммы тока и напряжения для модели (рис.2) представлены на рисунках 3 и 4 соответственно. Глядя на представленные осциллограммы видно, что изменение режима работы рассматриваемой системы изменяется в момент времени t=0,1 с. Именно в этот момент наблюдается переход нашей системы из одного установившегося состояние в другое (имеет место переходный процесс). При подключении БСК к сети наблюдается бросок тока, как было сказано ранее.
Литература:
- Балабанов, М. С. Выбор коммутационной аппаратуры для устройств компенсации реактивной мощности / М. С. Балабанов // Ползуновский вестник. — 2014. — № 4. — С. 28–34.
- Коваленко, Д. В. Неисправности батарей статических конденсаторов, возникающих при наличии высших гармоник в системах электроснабжения / Д. В. Коваленко // Молодой ученый. — 2016. — № 19 (123). — С. 69–72.
- Основы теории цепей / Г. В. Зевеке, П. А. Ионкин, А. В. Нетушил, С. В. Страхов. — Москва: Энергия, 1975. — 751 с.
- Тихончук, Д. А. Вероятность повторных пробоев в выключателях разных типах при коммутации батарей статических конденсаторов 110 кВ / Д. А. Тихончук // Промышленная энергетика. — 2013. — № 6. — С. 38–42.
- Тихончук, Д. А. Коммутация батареи статических конденсаторов высокого напряжения выключателем с одним приводом: диссертация на соискание ученой степени канд. техн. наук: 05.09.03 / Тихончук Дмитрий Александрович. — Уфа, 2014. — 232 с.

