Основная задача искусственной нейронной сеть Хэмминга [1] заключается в решении задач классификации бинарных входных векторов. В основе работы этой сети лежат процедуры, направленные на выбор в качестве решения задачи классификации одного из эталонных образов, наиболее близкого к поданному на вход сети зашумленному входному образу, и отнесение данного образа к соответствующему классу.
Классическая нейронная сеть Хэмминга может дать только один релевантный ответ в результате своей работы. В случае, если на самом деле имеется несколько ответов с одинаковой или относительно мало различающейся релевантностью, такой результат работы может оказаться нежелательным для практических нужд.
Способ модернизации нейронной сети Хэмминга, предложенный автором данной статьи, решает эту проблему.
Формальная постановка задачи.
Дано:
Обучающее множество ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Задача:
Надо построить сеть, реализующую такую функцию F(X), чтобы для любого ![]() , такого что (
, такого что (![]() ),
), ![]() ,…,
,…, ![]() , где
, где ![]() . Здесь
. Здесь ![]() – гиперпараметр нейронной сети (то есть параметр, настраиваемый вручную при конструировании сети). Этот гиперпараметр равняется максимальному количеству ответов нейронной сети. Также есть гиперпараметр ε, который будет использоваться в модуляторе (элементе нейронной сети Хэмминга, добавление которого является частью её модернизации).
– гиперпараметр нейронной сети (то есть параметр, настраиваемый вручную при конструировании сети). Этот гиперпараметр равняется максимальному количеству ответов нейронной сети. Также есть гиперпараметр ε, который будет использоваться в модуляторе (элементе нейронной сети Хэмминга, добавление которого является частью её модернизации).
Описание обучающего множества.
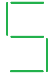
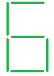
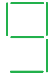
Обучающим множеством будет набор векторных представлений чисел, изображённых на рисунке 1. Каждый элемент любого такого вектора будет показывать, присутствует ли линия в графическом изображении номера, соответствующего этому вектору, на конкретной позиции, соответствующей этому элементу. К примеру, вектор, поставленный в соответствие графическому изображению цифры «0» из рисунка 1, имеет вид ![]() , а вектор, соответствующий цифре «5» –
, а вектор, соответствующий цифре «5» – ![]() .
.

Рис. 1. Примеры графических изображений цифр, составляющих обучающую выборку
Принцип работы и архитектура классической искусственной нейронной сети Хэмминга.
Нейронная сеть Хэмминга состоит из нескольких слоёв (см. рис. 2):
- Слой 1 – для вычисления расстояния Хэмминга.
- Слой 2 – слой MaxNet для выявления наименьшего расстояния Хэмминга.
- Слой 3 – слой, состоящий из пороговых функций для получения ответа вида: 1 для «победителя» (самого ближайшего объекта обучающей выборки по отношению к данному) и 0 для всех остальных.
- Слой 4 выходной слой, возвращающий вектор, поставленный в соответствие «победителю».
В первом, втором и третьем слоях находится столько нейронов [1], сколько было объектов в обучающей выборке. В последнем, выходном, слое находится столько нейронов, какова длина векторов, поставленных в соответствие объектам. Каждому из обучающих объектов ставится в соответствие нейрон первого слоя, веса которого инициализируются элементами вектора этого объекта. В слое MaxNet инициализируются веса связей между нейронами этого слоя следующими величинами:
- 1, если связь идёт из нейрона в него же самого,
-
случайной величиной из интервала
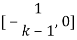 (
( – это количество обучающих примеров), если связь соединяет два различных нейрона. В выходном слое каждому нейрону поставлен в соответствие какой-либо элемент вектора объекта. И веса связей этого нейрона инициализируются либо -1, либо 1. Это зависит от того, какое значение имеет данный элемент вектора у объектов, соответствующих связям этого нейрона.
– это количество обучающих примеров), если связь соединяет два различных нейрона. В выходном слое каждому нейрону поставлен в соответствие какой-либо элемент вектора объекта. И веса связей этого нейрона инициализируются либо -1, либо 1. Это зависит от того, какое значение имеет данный элемент вектора у объектов, соответствующих связям этого нейрона.
Принцип работы заключается в том, что в слое MaxNet вычисляется объект обучающей выборки, ближайший к поданному на вход нейронной сети объекту, на основе данных о расстояниях, вычисленных в первом слое.
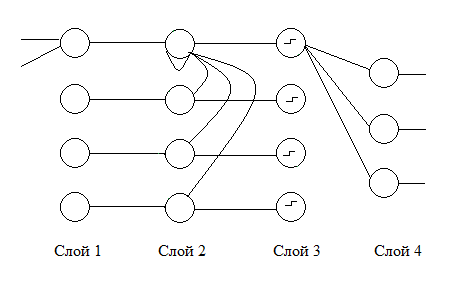
Рис. 2. Архитектура классической искусственной нейронной сети Хэмминга
Модернизация искусственной нейронной сети Хэмминга.
Помимо уже описанных элементов архитектуры сети появляются новые:
- модулятор понижения степени близости по расстоянию Хэмминг между предыдущим «победителем» и объектом, поданным на вход,
- временная память, хранящая изначальные расстояния от объектов обучающей выборки до объекта, поданного на вход (рис. 3).
Отличие этой нейронной сети от классической заключается в том, что проводится ![]() -ое количество запусков процесса соревнования в слое MaxNet. После каждого такого запуска «победитель» запоминается, и в начале следующего запуска его мера близости до объекта, поданного на вход, искусственно занижается на
-ое количество запусков процесса соревнования в слое MaxNet. После каждого такого запуска «победитель» запоминается, и в начале следующего запуска его мера близости до объекта, поданного на вход, искусственно занижается на ![]() . Таким образом, вероятность повторной победы «победителя» при следующем запуске снижается при условии, что существуют объекты обучающей выборки, мера близости от которых до поданного на вход объекта не превышает меру близости от этого объекта до «победителя».
. Таким образом, вероятность повторной победы «победителя» при следующем запуске снижается при условии, что существуют объекты обучающей выборки, мера близости от которых до поданного на вход объекта не превышает меру близости от этого объекта до «победителя».
Тестовые данные.
Модернизированная искусственная нейронная сеть Хэмминга с гиперпараметрами c = 3, ε = 0.3 была обучена на графических изображениях чисел от 0 до 9 (см. рис. 1) и протестирована на этих же изображениях и на изображениях, которые не являются изображениями чисел, но похожи на них. Результаты тестирования можно увидеть в таблице 1.
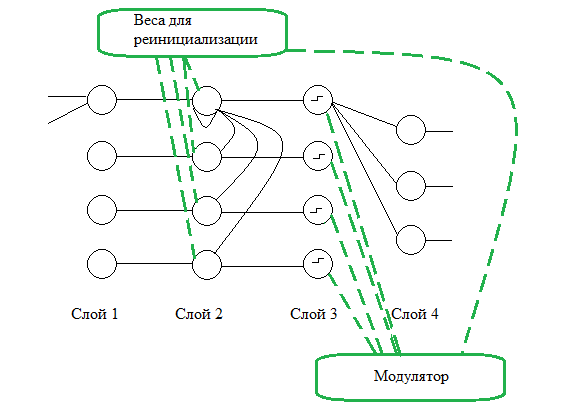
Рис. 3. Архитектура модернизированной искусственной нейронной сети Хэмминга
Таблица 1
Результаты тестирования модернизированной искусственной нейронной сети Хэмминга (с = 3, ε= 0.3)
|
Поданный на вход объект |
Первый ответ нейронной сети |
Второй ответ нейронной сети |
Третий ответ нейронной сети |
|
|
|
|
пропуск |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
пропуск |
Из таблицы 1 видно, что сеть для входных изображений находит наиболее похожие на них изображения из обучающей выборки, иногда эта сеть дважды выдаёт один и тот же ответ (в таком случае ставится пропуск), иногда сеть сначала выдаёт менее релевантные ответы (это может быть обусловлено случайным фактором выбора весов).
Программную реализацию варианта модернизации нейронной сети Хэмминга, предложенной автором данной статьи, можно найти по следующей ссылке https://github.com/alex27594/hamming_neural_network.git.
Литература:
- Круглов В. В., Борисов В. В. Искусственные нейронные сети. Теория и практика. — 2-е изд., стереотип. — М.: Горячая линия-Телеком, 2002. — 382 с.