Термин вейвлет ввели в своей статье Гроссманн и Морле в середине 80-х годов XX века связано было это с анализом свойств сейсмических и акустических сигналов. Их работа стала началом интенсивного изучения вейвлетов в последующее десятилетие рядом таких учёных, как Добеши (Dobechies), Мейер (Meyer), Малл (Mallat), Фарж (Farge), Чуи (Chui) [1].
В переводе с английского wavelet — всплеск. Вейвлеты представляют собой функции в виде маленьких волн (всплесков) с нулевым интегральным значением и имеющими локализацию по оси переменной (t или x), способность к сдвигу и масштабированию (сжатию или растяжению).
Существует большое разнообразие типов вейвлетов. Но на практике пользуются вейвлетом Хаара. Так как он является самым простым и хорошо локализованным во временной области.
Мы же в дальнейшем будем пользоваться вейвлетом Добеши. Данный вейвлет является несимметричным и широко используемым на практике.
В настоящее время большую популярность для анализа нестационарных режимов в электроэнергетике приобрело вейвлет-преобразование. Существует несколько видов вейвлет-преобразований.
Но в основе любого лежат две непрерывных и зависящих друг от друга функции, которые интегрируются по некоторой переменной. Эти функции носят названия вейвлет-функции и масштабирующей функцией.
Для наглядности понимания двух функций рассмотри самый простой тип вейвлета- вейвлет Хаара. На рисунке 1 представлены масштабирующая и детализирующая функции (вейвлет-функция) вейвлета Хаара.
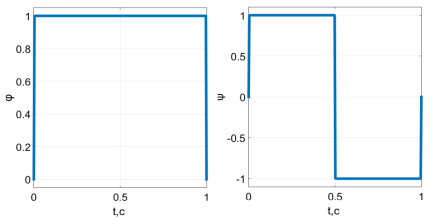
Рис. 1. Масштабирующая и детализирующая функции вейвлета Хаара
Также приведём данные функции и для вейвлета Добеши второго порядка, представленные на рисунке 2.
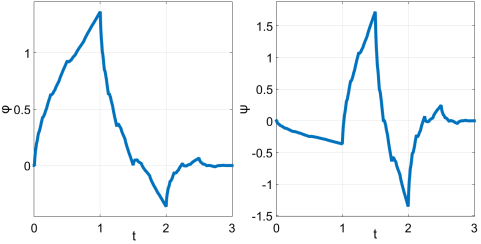
Рис. 2. Масштабирующая и детализирующая функции вейвлета Добеши
Проблема высших гармоник и интергармоник в электроэнергетике.
Внимание в данный момент приобретает обеспечение качества электроэнергии, которая должна соблюдать определённые требования. Из-за постоянного роста количества электрических приёмников возникают высшие гармоники. А составляющие гармоник тока и напряжения ведут в свою очередь к возникновению проблем качества электрической энергии. Когда происходит отклонение напряжения от номинального значения происходит увеличение потребляемой мощности. То есть наличие в сигналах высших гармоник и интергармоник ведёт к увеличению мощности.
Эффекты, вызываемые высшими гармониками напряжения и тока.
Все эффекты можно разделить на две группы: мгновенного и длительного возникновения.
Проблемы мгновенного возникновения включают:
1. Искажение формы питающего напряжения.
2. Падение напряжения в распределительной сети.
3. Эффект гармоник, кратных трем.
4. Резонансные явления на частотах высших гармоник.
5. Повышенный акустический шум в электромагнитном оборудовании.
6. Вибрация в электромашинных системах.
Проблемы длительного возникновения включают:
1. Нагрев и дополнительные потери в трансформаторах и электрических машинах.
2. Нагрев конденсаторов.
3. Нагрев кабелей распределительной сети.
Интергармоники также, как и высшие гармоники оказывают влияние на электроэнергетическую систему, но их влияние всё же сильнее. Так как из-за появления интергармоник образуются потери мощности электрической энергии.
Источниками интергармоник являются люминесцентные лампы, сварочные аппараты, электроприводы и др. (рисунке 3).
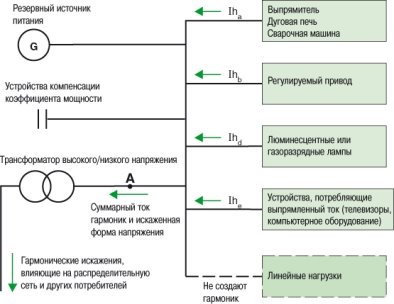
Рис. 3. Источники интергармонических составляющих
Согласно ГОСТу 32144–2013 нормирование интергармонки в России не производится.
Поэтому для исследования показателей качества электроэнергии большое значение имеет идентификация как высокочастотных составляющих, так и интергармонических.
Идентификация высокочастотных составляющих.
Собрав имитационную модель узла нагрузки системы электроснабжения в Matlab и Simulink. Используя литературу [2]. Снимем с показаний осциллографа графики токов и напряжений, которые представлены на рисунке 4.
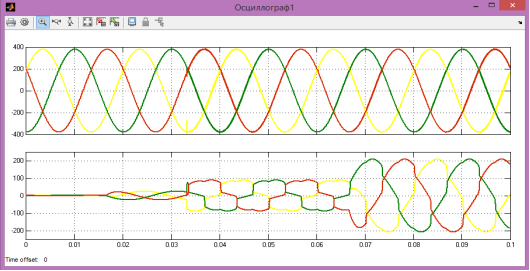
Рис.4. Графики токов и напряжений, снятые с показания осциллографа
На рисунке 4 изображены графики токов и напряжений. Отметим, что на графике токов явно выражено влияние нелинейной нагрузки. А на графике напряжений наличие гармоник невозможно увидеть. Попробуем решить эту проблему с помощью вейвлет-преобразования.
Проведём вейвлет-преобразование полученных сигналов тока (рисунок 6) и напряжения (рисунок 5) вейвлетом Добеши второго порядка (db2) до 5 уровня.
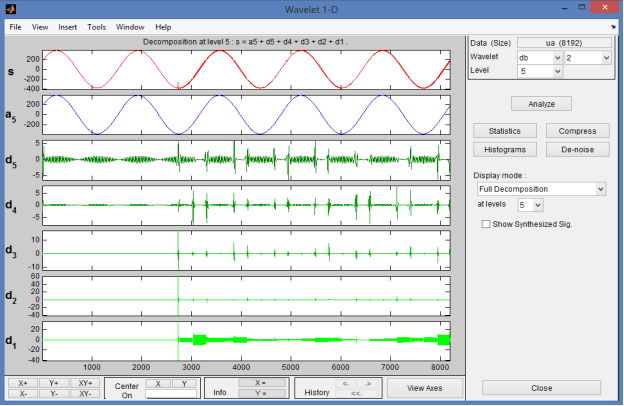
Рис. 5. Разложение сигнала напряжения
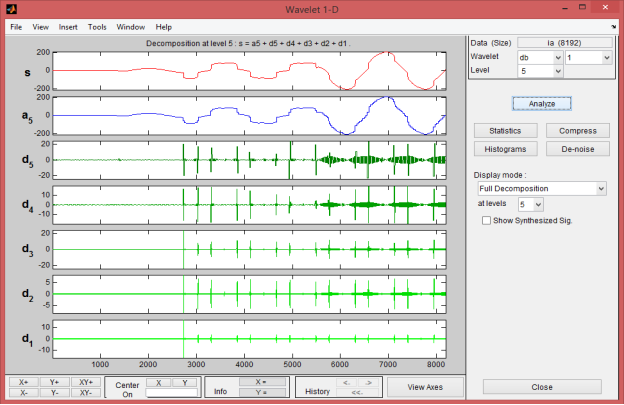
Рис. 6. Разложение сигнала тока
Поэтому мы заметили, что при вейвлет-преобразовании учитываются гармонические составляющие как в графике тока, так и в графике напряжения. Также при использовании вейвлет-преобразования мы можем определить точное время, когда происходит изменение нормального режима, то есть подключение нагрузки. Наличие нагрузки заметно на амплитудном значении тока и подключение нелинейной нагрузки, которая видна по искажению кривой тока.
Вывод.На данный момент важным является обеспечение качества электроэнергии, которая должна соблюдать определённые требования. Из-за постоянного роста количества электрических приёмников возникают высшие гармоники. В данной статье показано, что с помощью вейвлет-преобразование можно обнаружить высокочастотные составляющие и избежать негативного влияния.
Литература:
- Дьяконов, В. П. От теории к практике. Вейвлеты [Текст]: учебное пособие / А. Н. Дьяконов. — М: Салон-Р. — 2003. — 440 с.
- Черных, И. В. Моделирование электротехнических устройств в MatlabSimPowerSystems и Simulink [Текст] / И. В. Черных. — М.: ДМК Пресс. — 2007. -288 с.







