В представленной работе рассматривается метод получения концентрации свободных носителей заряда в сильнолегированном азотом карбиде кремния политипа 4H. Определение концентрации осуществляется путем рассмотрения спектра отражения, полученного с помощью фурье-спектроскопии, исследуемого образца карбида кремния. Для точного определения используется моделирование в математическом пакете Mathcad.
Ключевые слова: карбид кремния, легирование, фурье-спектроскопия, спектр отражения, моделирование, плазменный резонанс, Mathcad, концентрация свободных носителей заряда
На сегодняшний день карбид кремния, в основном, используется в силовой электронике, микроэлектронике специального назначения, полупроводниковой элементарной базе, работающих в экстремальных условиях. Таким образом очень важно проводить качественный анализ карбида кремния, использующегося в данных устройствах. Это возможно с помощью фурье-спектроскопии.
- Карбид кремния.
Карбид кремния является неорганическим бинарным химическим соединением кремния и углерода, при взаимодействии, образующих непрямозонную полупроводниковую кристаллическую структуру.
1.1 Политипизм.
Политипизм является частным случаем полиморфизма и наблюдается в некоторых кристаллах со слоистой структурой. Политипные модификации построены из одинаковых слоев или слоистых «пакетов» атомов и различаются способом и периодичностью наложения таких пакетов или слоев. Известно, что карбид кремния при комнатных температуре и давлении, может существовать в виде различных политипных форм. На данный момент количество известных политипов кремния составляет около двухсот пятидесяти в любом политипе карбида кремния сохраняется ближний порядок, то есть атом углерода, находится в тетраэдрическом окружении атомов кремния и наоборот. Воспроизведение того или иного политипа зависит от многих факторов таких как: температура и скорость роста, состав кристаллизационной среды, тип легирующих примесей и др. [1]
1.2 Свойства карбида кремния.
− Большая ширина запрещенной зоны (варьирующаяся от 2,3 до 3,3 эВ для различных политипов) — данное свойство обеспечивает, приборам, созданным на основе SiC, работу в большом интервале температур, а также способность излучать в диапазоне от 0.38 до 0.78 микрометров [2].
− Теплопроводность (3–5 Вт/см2). Благодаря высокой теплопроводности SiC, приборы могут работать при больших плотностях тока и высоких уровнях мощности, эффективно рассеивая избыток тепла.
− Термическая стабильность, характеризуемая температурой Дебая. Данная характеристика определяет температуру, при которой возникают упругие колебания кристаллической решетки с максимальной частотой. При превышении данной температуры, колебания могут стать неупругими, что приведет к разрушению материала.
− Наличие собственной подложки, которая может иметь проводимость n или p типа, также у карбида имеется собственный окисел SiO2.Это способствует тому, что на основе SiC можно создавать любые типы полупроводниковых структур, которые могут быть использованы в создании приборов в областях микро, СВЧ, мощной и сильноточной электроники, фотодетекторов, фото — электро — преобразователей ультрафиолетового излучения.
− Радиационная стойкость (за счет высокой энергии дефектообразования 25 –35 эВ) — означает, что параметры полупроводника или прибора который на нем основываются останутся неизменными при взаимодействии с радиоактивным излучением. При облучении полупроводников возникают радиационные дефекты — глубинные центры в полупроводнике акцепторной или донорной природы. Если рассматривать полупроводник n типа, то в результате облучения, возникает радиационный дефект акцепторной природы и электроны из зоны проводимости переходят на этот уровень. Вследствие этого проводимость материала уменьшается, при больших дозах облучения полупроводник может стать изолятором [3].
- Спектроскопия.
Спектрометр — это оптическое устройство, предназначенное для регистрации и исследования оптических спектров в ультрафиолетовой, видимой и инфракрасной областях. Обработка которых, необходима для таких видов деятельности как: количественный анализ и контроль качества продукции в химической, нефте — химической, фармацевтической, пищевой и парфюмерной промышленности, осуществление экологического контроля, криминалистическая и другие виды экспертиз, также данное устройство используется для качественного и количественного анализа выращенных кристаллических структур, использующихся в полупроводниковой промышленности.
2.1 Фурье-спектрометр.
В основе работы любого фурье-спектрометра лежит явление интерференции электромагнитного излучения. Главным элементом оптической схемы фурье-спектрометра является интерферометр Майкельсона. Он позволяет получить интерферограмму — сигнал, регистрируемый в зависимости от оптической разности хода лучей. С помощью преобразования Фурье из полученной интерферограммы можно вычислить спектр, с помощью которого получается информация о оптических свойствах исследуемых образцов [4]. На рисунке 1 изображена упрощенная схема фурье-спектрометра (Vertex 80 Bruker) на котором проводилось исследование.
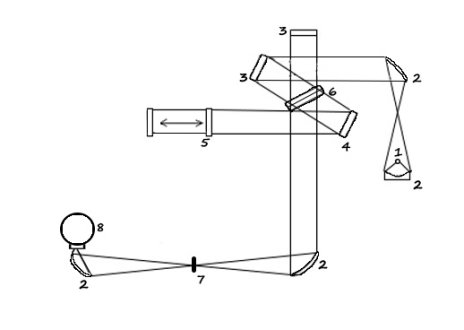
Рис. 1. 1 — Источник света; 2 — Параболические зеркала; 3 — Плоские зеркала; 4 — Подстроечное зеркало; 5 — Подвижное зеркало; 6 — Светоделитель; 7 — Кювета с исследуемым образцом; 8 — Детектор
2.2 Исследуемый образец карбида кремния.
Исследуемый образец представляет собой толстую пластину сильнолегированного монокристаллического карбида кремния черного цвета выращенного по методу ЛЭТИ. Ввиду того, что данный образец сильно поглощает свет в ультрафиолетовом, видимом и ближнем и среднем инфракрасном диапазонах, исследование его свойств по спектрам поглощения не представляется возможным.
2.3 Явление плазменного резонанса.
Плазменный резонанс — обуславливается колебанием свободных носителей заряда относительно решетки с некой частой:
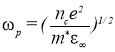 ,(1)
,(1)
где nc — концентрация свободных носителей заряда (см-3); m* — эффективная масса свободных носителей заряда (кг) (const); e — заряд электрона (Кл); ![]() – оптическая диэлектрическая постоянная (const). [5]
– оптическая диэлектрическая постоянная (const). [5]
Таким образом, плазменный резонанс напрямую зависит от концентрации свободных носителей заряда. На спектре отражения в ик области, изображенного на рисунке 2, частоту плазменного резонанса можно наблюдать в области, находящейся за фононной областью отражения.
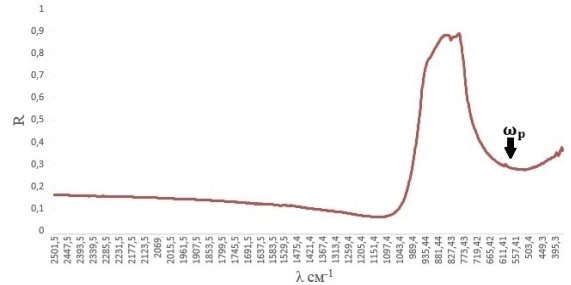
Рис. 2. Положение частоты плазменного резонанса в сильнолегированном азотом карбиде кремния (4H)
- Нахождение концентрации свободных носителей заряда по спектру отражения.
Если подробней рассмотреть формулу № 1, можно заключить, что все параметры кроме частоты плазменного резонанса и концентрации свободных носителей заряда являются константами. Таким образом, получение величины концентрации собственных носителей заряда возможно только с помощью точного определения частоты плазменного резонанса.
3.1 Моделирование спектра отражения.
Для получения величины частоты плазменного резонанса необходимо смоделировать имеющийся спектр в математическом пакете Mathcad, путем вывода коэффициента отражения, и вычисления волновых чисел из уравнения диэлектрической проницаемости [5]:
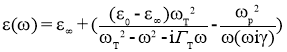 ,(2)
,(2)
где ε(ω) — относительная диэлектрическая проницаемость;
Для определения концентрации в легированным азотом карбиде кремния по спектру отражения, очень важно смоделировать спектр отражения так, чтобы он максимально совпадал с экспериментальным, поэтому для расчета коэффициента отражения используется метод наименьших квадратов:
![]() ,(3)
,(3)
где R — коэффициент отражения; n — коэффициент преломления; k — коэффициент экстинкции;
Чтобы обеспечить правильность расчета, коэффициенты преломления и экстинкции должны рассчитываться из формулы комплексной относительной диэлектрической проницаемости [1]:
![]() (4)
(4)
ε1 — вещественная часть относительной диэлектрической проницаемости; ε2 — мнимая часть относительной диэлектрической проницаемости;
![]() (5)
(5)
![]() (6)
(6)
Путем решения приведенной выше системы уравнений, получаем выражение для коэффициента преломления:
![]() (7)
(7)
С помощью дальнейших вычислений получаем корни данного уравнения:
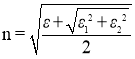 (8)
(8)
И следующий из него коэффициент экстинкции:
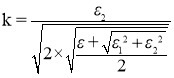 (9)
(9)
Для построения смоделированного спектра отражения необходимо задать три неизвестных переменных (![]() ), притом отклонение расчетного коэффициента отражения должно стремиться к значению близкому к нулю (метод наименьших квадратов), для обеспечения правильного построения спектра. Важно обратить внимание, что среди неизвестных переменных имеется частота плазменного резонанса, это позволяет в случае верно смоделированного спектра использовать полученное значение частоты для расчета концентрации свободных носителей заряда. Ниже приведены экспериментальный и смоделированный спектры.
), притом отклонение расчетного коэффициента отражения должно стремиться к значению близкому к нулю (метод наименьших квадратов), для обеспечения правильного построения спектра. Важно обратить внимание, что среди неизвестных переменных имеется частота плазменного резонанса, это позволяет в случае верно смоделированного спектра использовать полученное значение частоты для расчета концентрации свободных носителей заряда. Ниже приведены экспериментальный и смоделированный спектры.
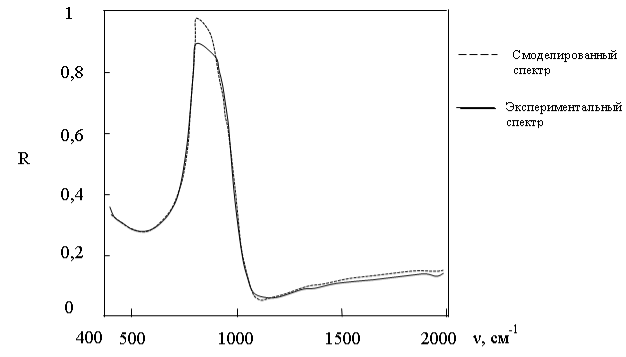
Рис. 3. Экспериментальный и смоделированный в Mathcad спектры сильнолегированного азотом 4H карбида кремния
Заключение.
Данный метод позволяет получить концентрацию свободных носителей заряда для сильнолегированного азотом карбида кремния с помощью спектра отражения. Особенность данного метода состоит в том, что он достаточно прост для воспроизведения, а также является весьма точным. Для исследуемого образца была найдена частота плазменного резонанса 639,2 см-1 и следующая из неё величина концентрации свободных носителей заряда 1,59×1019.
Литература:
- Пихтин А. Н. Оптическая и квантовая электроника: учебник для вузов. Москва: Издательство «Высшая школа», 2001. 573 с.
- Карбид кремния: технология, свойства, применение / О. А. Агеев, А. Е. Беляев, Н. С. Болтовец, В. С. Киселев, Р. В. Конакова. Харьков: Издательство «ИСМА», 2010. — 532 с.
- Радиационная стойкость широкозонных полупроводников (на примере карбида кремния) / А. А. Лебедев, В. В. Козловский, Н. Б. Строкан, Д. В. Давыдов, А. М. Иванов и др. СПб.: Физика и техника полупроводников, 2002, том 36, вып. 11.
- Инфракрасная спектроскопия / И. В. Колесник, Н. А. Саполетова. Москва: Издательство «МГУ им М. В. Ломоносова», 2011. — 88 с.
- Уханов Ю. И. Оптические свойства полупроводников СПб.: Издательство «Наука», 1977. 139–338 с.
- Spectroscopic analysis of electrical properties in polar semiconductors with over — damped plasmons / S. Nakashima, H. Harima // Journal of Applied Physics. 2004, Vol. 95, № 7, pp. 3541–3546.







