В начале данной статьи рассматриваются основные принципы и геометрия плазмонных взаимодействий на границе проводящей и диэлектрической среды. Далее предлагается математическая модель и алгоритм для моделирования спектров плазмонных взаимодействий. В завершении статьи представлена компьютерная программа для моделирования плазмонных спектров.
Ключевые слова: плазмоника, плазмонные спектры, динамическая проводимость, поверхностные электромагнитные волны, динамический коэффициент распространния, математическое моделирование
Сегодня весь земной шар опутан оптическими волокнами, по которым передаются колоссальные потоки информации, закодированной в световых сигналах. Устройства, манипулирующие видимым светом и другими электромагнитными волнами, могли бы прийти на смену электронным цепям в микропроцессорах и других микросхемах. Однако, одним из существенных недостатков такой передачи является фундаментальное ограничение, связанное с дифракционным пределом, который определяет минимальный размер оптических элементов передачи (половина длинны волны передаваемых волн).
Одним из вариантов «обхода» данного ограничения является использование плазмонных взаимодействий на границе раздела металл-диэлектрик. В 1980-х гг. было экспериментально установлено, что при определенных условиях между световыми волнами, направленными на границу раздела между металлом и диэлектриком, и подвижными электронами на поверхности металла возникает резонансное взаимодействие. Иными словами, электроны начинают колебаться в такт с колебаниями электромагнитного поля над металлом. В результате возникают поверхностные плазмоны.
Базовые принципы плазмоники
Падающий свет на рисунке 1 проходит сквозь прозрачную среду 1 с относительно большим показателем преломления, и попадает на тонкую металлическую пленку 2 под углом, превышающим угол полного внутреннего отражения. Часть света проникает в металл и возбуждает колебания свободных электронов металла (электронной плазмы). И в этой плазме возникают поверхностные плазмонные волны.
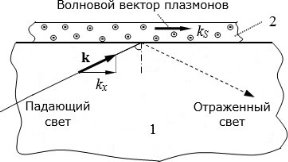
Рис. 1. Схема оптического возбуждения поверхностных плазмонов. 1 — прозрачная среда с высоким показателем преломления; 2 — тонкая металлическая пленка
Одной из главных проблем, препятствующей использования поверхностных плазмонов в проектировании и при изготовлении современных микросхем является относительно быстрое затухание плазмонной волны (порядка нескольких десятков нанометров) на поверхности полупроводника. Существует несколько путей решения данной проблемы. Одним из них является нахождение оптимальных длин волн, а следовательно и частот, излучения для возбуждения поверхностных плазмонов. Для этих целей далее предложен метод расчета плазмонных спектров, а также представлена компьютерная программа выполняющая расчеты данным методом.
Математическое моделирование плазмонных спекров
Для моделирования плазмонных эффектов была выбрана относительно простая структура изображённая ни рисунке 2.
Тонкая плёнка, состоящая из одного либо нескольких атомных слоёв исследуемого материала, нанесена на полупроводниковую подложку. По направлениям осей z и x подложка считается условно бесконечной, а по направлению оси y имеет ширину — d.
Дисперсионное уравнение для двумерных плазмонных волн распространяющихся по поверхности данной структуры имеет вид:
(1)
где 
волновой вектор, 
частота плазмонной волны, 
— диэлектрическая постоянная окружающей среды, 
— диэлектрическая постоянная полупроводниковой подложки, 
— динамическая проводимость исследуемого полупроводникового слоя.
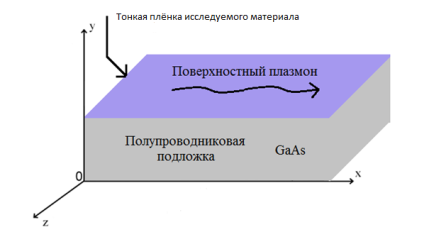
Рис. 2. Схематическое представление базовой структуры для моделирования плазмонных эффектов
Из выражения (1) следует, что значение волнового вектора, а следовательно, и длинна затухания напрямую зависят от динамической проводимости (зависимой от частоты) полупроводникового слоя. В случае моноатомного слоя исследуемого материала динамическая проводимость равна [1]:
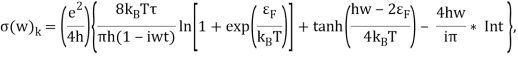(2)
где e — заряд электрона, h — редуцированная постоянная планка, kB — постоянная Больцмана, 
и T — время свободного пробега и температура газа носителей заряда в исследуемом материале, 
— эффективная энергия Ферми, Int определяется выражением:
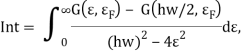(3)
определяется выражением:
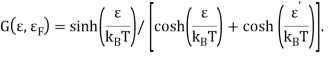(4)
Решай уравнения Максвелла для данной структуры получаем [2]:
(5)
где n — коэффициент преломления среды, 
— комплексный индекс распространения, c — скорость света, 
электрическая постоянная.
Решая уравнение (5) относительно 
, становится возможным найти коэффициент распространения Re() и коэффициент абсорбции (усиления) q = Im()*w/c, который фактически и является плазмонным спектром. В случае когда коэффициент преломления среды n равен единице получаем:
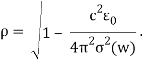(6)
Программа для расчета плазмонных спектров
Ввиду сложности расчетов плазмонных спектров на большом диапазоне частот вручную, была написана компьютерная программа по расчету и графическому представлению спектров, а также некоторых других параметров представленной выше структуры. В качестве платформы для написания программы была выбрана платформа Microsoft.NET 4.
Данная программа предназначена для расчета следующих параметров:
– значений действительной и мнимой части комплексной проводимости;
– значений действительной и мнимой части коэффициента поверхностного распространения плазмонных волн;
– значения коэффициента абсорбции поверхностных плазмонных волн.
Все вышеперечисленные значения рассчитываются в зависимости от следующих входных параметров:
– диапазон входных частот;
– количество контрольных расчётных точек (количество шагов);
– количества моноатомных слоёв нанесённых на полупроводниковую подложку;
– энергии Ферми () каждого из моноатомных слоёв;
– времени свободного пробега (
) носителей заряда в каждом из моноатомных слоёв;
– температура газа свободных носителей заряда (T) в каждом из моноатомных слоёв;
– параметры аппроксимации некоторых используемых функций
На рисунке 3 проиллюстрирована работа программы: в верхнем левом углу изображен график зависимости комплексной динамической проводимости от частоты, в нижнем левом — зависимость комплексного коэффициента проводимости от частоты, в верхнем правом зависимость коэффициента адсорбции от частоты, что фактически является плазмонным спектром.
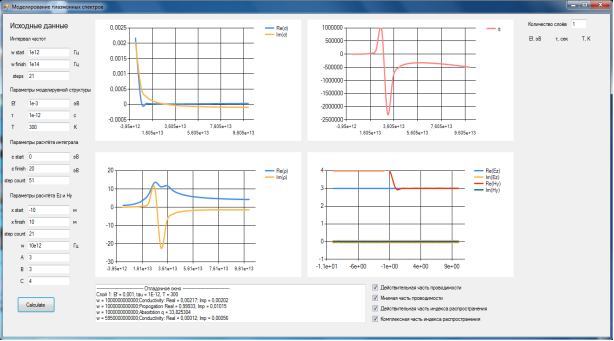
Рис. 3. Программа для моделирования плазмонных спектров
Заключение
На сегодняшний момент использование поверхностных плазмонных взаимодействий на границе диэлектрической и проводящей среды является перспективным направлением для дальнейшего развития быстродействия вычислительной техники.
Литература:
- Мельников В. С., Полищук О. В., Попов В. В. Полное преобразование поляризации терагерцового излучения массивом графеновых микролент без использования магнитного поля // Изв. Сарат. ун-та. Нов. сер. Сер. Физика. 2015. Т.15, вып. 3.
- Dubinov A. A., Aleshkin V. Ya., Mitin V., Otsuji T., Ryzhii V. Terahertz surface plasmons in optically pumped graphene structures // J. Phys.: Condens. Matter. 2011. V. 23. P. 145302.
