В данной работе была рассмотрена многошаговая задача поиска неподвижного объекта, спрятанного среди n коробок, за k шагов, в которой обучающийся ищущий стремится минимизировать затраты ресурсов, требуемые на нахождение объекта при условии, что вероятность найти объект при просмотре верной коробки не равна единице. Обучаемость ищущего заключается в запоминании коробок, в которых уже был произведен поиск. Была рассмотрена математическая модель данной задачи для поиска объекта, находящегося в одной из n коробок, за k шагов, основанная на принципе оптимальности Беллмана и состоящая из k рекуррентных уравнений. После был реализован программный алгоритм решения данной задачи для случая n коробок и k шагов на языке программирования C#, после чего был произведен анализ некоторых решений.
Поиск различных объектов издревле представляет собой одну из ключевых сторон человеческой активности. В работе [1] процесс поиска определяется как целенаправленное обследование конкретной области пространства для обнаружения находящегося там объекта. Обнаружением объекта можно считать получение информации о его местоположении путем установления с ним прямого энергетического контакта. Это вполне естественная проблема, с которой мы сталкиваемся на ежедневной основе. К примеру, перед тем как уходить утром на работу, необходимо собрать определенный набор вещей (ключи, кошелек, документы), которые в свою очередь необходимо локализовать. Их местоположение многообразно, и есть потребность свести количество времени, затраченное на поиск, к минимуму. Отходя от подобных бытовых проблем, можно расширить список задач до локализации поврежденных файлов компьютера, разведки месторождений нефти или поиска заблудившегося в лесу человека.
Одним из путей исследования поиска является построение и анализ математических моделей, отображающих объективные закономерности поиска и позволяющие установить связь между условиями его выполнения и его результатами, с целью дальнейшего анализа критериев эффективности поиска.
Полное и систематическое изложение теории решения поисковых задач было приведено в работах [2,4]. Следует заметить, что в мировой литературе по теории игр существует очень много работ в этой области прикладной математики, однако все еще остаются нерешенными задачи даже в самых простых случаях. И здесь вопрос связан со сложностью решения уравнения Беллмана для задач большой размерности.
В данной работе речь пойдет о многошаговой задаче поиска неподвижного пассивного объекта в дискретной среде, идеей для рассмотрения которой послужила статья [3]. Многошаговость задачи обусловлена повторяющейся процедурой поиска.
Постановка задачи
Пусть дано дискретное множество местоположений объекта (в дальнейшем, коробок). Игрок H выбирает коробку и прячет в ней объект. Игрок S пытается обнаружить его. Событие, заключающееся в обнаружении объекта при просмотре верной коробки, не достоверное, т. е. объект может быть не найден, даже если он был в этой коробке. Каждый просмотр коробки требует затрат некоторых ресурсов (например, энергии или времени). Поиск продолжается до исчерпания числа попыток. При нахождении предмета игрок S вознаграждается. Игрок S стремится свести затраты своих ресурсов к минимуму.
В данной работе поставлены следующие задачи:
- Составить теоретико-игровую модель рассматриваемой задачи с обучающимся ищущим, т. е. ищущий располагает информацией, в каких коробках уже был произведен поиск, и на основе этой информации осуществляет следующий шаг;
- Обеспечить программную реализацию, способную решать данную задачу для k-шагового поиска объекта в N коробках;
- Проанализировать решения некоторых задач.
Построение модели
Игрок H выбирает одну из N коробок, пронумерованных от 1 до N, и прячет в ней объект. Игрок S осуществляет поиск объекта в одной из них. Каждый просмотр i-й коробки,
может быть осуществлен путем затрат ресурса 
. Также определим вероятность 
обнаружить объект в коробке i, при условии, что он в ней находится. Если игрок S находит объект, он получает вознаграждение в виде величины 
.
Обозначим за 
смешанную стратегию игрока H. Игрок S имеет представление о стратегии игрока H. Зная его, он стремится пройти через серию поисков с минимальными затратами. Обозначим за 
минимальные ожидаемые затраты игрока S на n-м шаге поиска и составим соответствующее нашим условиям уравнение Беллмана минимальных ожидаемых затрат :
(1)
где 
Вектор 
отвечает за способность игрока S обучаться в процессе поиска. Осуществляя неудачный поиск в какой-либо коробке, игрок запоминает, что в этой коробке предмета найдено не было и, в связи с этим, меняет приоритеты поиска в сторону остальных коробок. Новые вероятности 
определяются в соответствии со следующими формулами:
(2)
Строго говоря, вектор являет собой апостериорную вероятность распределения объекта по коробкам при условии, что был произведен неудачный просмотр i-й коробки. Иными словами, вероятность того, что объект находится в i-й коробке после произведенного в ней неудачного поиска, уменьшится, в то время как вероятности нахождения объекта в остальных коробках увеличатся.
Пользуясь уравнениями (1), (2) можно определить минимальные потери 
игрока S на шаге n, в том случае, если он производил поиски по оптимальной последовательности коробок 
.
Программная реализация
Программная реализация поставленной задачи была произведена при помощи языка программирования C#. Основную сложность в процессе реализации составила способность к обучению игрока S, т. е. изменение вектора 
распределения объекта по коробкам в ходе игры. Вследствие этого возникает большое количество различных векторов 
. К примеру, в задаче поиска объекта среди трех коробок, уже на 3-м шаге будет 27 возможных вариантов выбора коробки (см. Рис. 1). В связи с этим, алгоритм программы оказался чрезвычайно ресурсоемким (запоминание и оперирование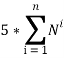 
количеством переменных), что сильно ограничивает класс доступных решению задач, ввиду недостаточной мощности ЭВМ, на которой производились вычисления.
На вход программы подаются значения: N — число коробок, n — число шагов, t — затраты ресурсов, a — выигрыш игрока S, вектор вероятностей p и вектор x. На выходе получаем значения оптимальных затрат
и оптимальный путь поиска по коробкам.
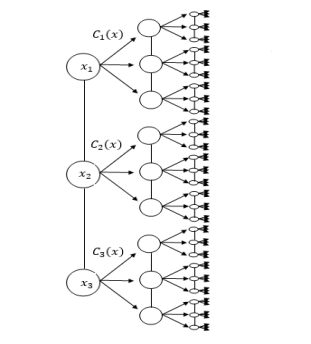
Рис. 1: Поиск среди 3-х коробок
Анализ численных примеров
Пример 1
Рассмотрим задачу за следующими условиями:
В результате работы программы получаем следующие значения:
Произведем вычисления функции минимальных затрат для значений
и рассмотрим зависимость прироста функции минимальных затрат от количества шагов игры. Результаты приведены в таблице 1. Как можно видеть, значения функции прироста являются убывающей последовательностью, что говорит о том, что функция минимальных затрат предположительно может быть ограничена сверху, т. е. затраты ресурсов, необходимых на поиск, могут быть ограничены. К сожалению, установить дальнейшее поведение последовательности прироста не удалось, ввиду невозможности решать данную задачу для большего числа шагов (т. к. ресурсоемкость алгоритма превысила имеющуюся). Из имеющихся данных можно выдвинуть два предположения:
- Функция прироста стремится к нулю, т. е. функция минимальных затрат имеет предел сверху;
- Функция прироста может принимать отрицательные значения, т. е. функция минимальных затрат начинает убывать после некоторого n.
Пример 2
Рассмотрим задачу за следующими условиями:
В результате работы программы получаем следующие значения:
Отрицательные затраты на поиск будем называть выгодой игрока S. Аналогично примеру 1 произведем вычисления для . Из представленных результатов в таблице 2 можно сделать вывод о том, что игроку S выгодно искать объект дольше, т. к. его выгода от этого только лишь увеличится. Численно установить наличие ограниченности снизу у функции минимальных затрат не удалось ввиду превышения ресурсоемкости. Более того, функция прироста ведет себя неоднозначно (наличие скачков).
Таблица 1
Результаты примера 1
|
n |
|
|
|
1 |
4.4296 |
- |
|
2 |
8.1622 |
3.7326 |
|
3 |
11.2042 |
3.042 |
|
4 |
13.5754 |
2.3712 |
|
5 |
15.3034 |
1.728 |
|
6 |
16.68715 |
1.38375 |
|
7 |
17.81158 |
1.12443 |
Таблица 2
Результаты примера 2
|
n |
|
|
|
1 |
0.04368 |
- |
|
2 |
0.2886 |
0.24492 |
|
3 |
-0.5334 |
-0.822 |
|
4 |
-1.8918 |
-1.3584 |
|
5 |
-3.7338 |
-1.842 |
|
6 |
-3.8673 |
-0.1335 |
|
7 |
-4.17878 |
-0.31148 |
Пример 3
Рассмотрим задачу за следующими условиями:
В результате работы программы получаем следующие значения:
В данном примере игрок S знает, что объект наиболее вероятно расположен в 4-ой коробке (
), однако найти его там довольно сложно (
). В результате видно, что игроку S выгодно совсем не обыскивать 4-ю коробку, а отдать предпочтения другим коробкам.
Выводы
В результате анализа численных решений ряда задач были сделаны следующие выводы:
– Игроку S в процессе поисков порой выгодно вовсе игнорировать ту коробку, в которой объект наиболее вероятно находится;
– В данном классе задач существует подкласс, в котором игроку S выгодно искать объект как можно дольше, т. к. его выгода от этого только лишь увеличится. Численно установить наличие предела выгоды в подобных задачах не удалось ввиду недостатка ресурсоемкости ЭВМ;
– В данном классе задач существует подкласс, в котором прирост функции затрат игрока S с ростом шагов является убывающей последовательностью, т. е. затраты могут быть ограничены. Справедливость этого утверждения для большого числа шагов в данных задачах установить не удалось.
Литература:
- Абчук В. А., Суздаль В. Г. Поиск объектов. М.: Сов. радио, 1977. 336 c.
- Петросян Л. А, Гарнаев А. Ю. Игры поиска. СПб.: Изд-во СПбГУ, 1992. 216 c.
- Gal S. A discrete search game // SIAM J. Appl. Math. 1974. Vol 27. No 4, P. 641–648.
- Garnaev A. Search Games and Other Applications of Game Theory.Heidelberg, N-Y.: Springer, 2000. 145 c.
