В статье обоснованы основные параметры вертикальных ножей на плоскорежущей лапе комбинированного рыхлителя, обеспечивающие агротехнические требования технологического процесса послойной обработки солонцов при наименьших тяговых сопротивлениях.
Ключевые слова: разрушение столбцов, просыпание гумуса, вынос неплодородного слоя на поверхность поля, вспушенность, резание почвы, тяговое сопротивление, высота и углы заточки и установки ко дну борозды вертикального ножа.
Лемех плоскорежущей лапы, подрезая солонцовый горизонт, частично крошит его нижнюю часть, а верхняя часть этого горизонта остается без изменения [1, с. 36]. Слабое разрушение данной части объясняется тем, что влажность его всегда низкая и для разрушения требуется большее напряжение. Поэтому для разрушения монолитности горизонта необходимы дополнительные деформаторы в виде вертикальных ножей (рис.1).
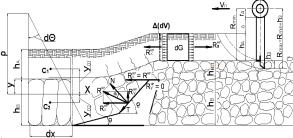
Рис. 1. Расчетная схема к обоснованию технологии послойной обработки комбинированного рыхлителя
Необходимая степень разрушения данного горизонта зависит от высоты и расстояния между вертикальными ножами [2, с. 42]. Технологический процесс послойной обработки обеспечивается при высоте ножей-рыхлителей не больше глубины обработки и не меньше мощности солонцового и подсолонцового горизонтов (рис. 1).
![]() , (1)
, (1)
где ![]() – глубина обработки, м;
– глубина обработки, м;
![]() – высота вертикального ножа, м;
– высота вертикального ножа, м;
![]() – мощность солонцового и подсолонцового горизонтов, м.
– мощность солонцового и подсолонцового горизонтов, м.
Высота вертикального ножа с учетом мощности верхнего слоя равна
![]() , (2)
, (2)
где ![]() – мощность верхнего слоя, м;
– мощность верхнего слоя, м;
При перемещении почвы по поверхности лемеха происходит частичное крошение нижнего слоя, в результате чего высота профиля пласта почвы увеличивается на величину, равную вспушенности ![]() . Тогда высота вертикального ножа с учетом вспушенности определяется выражением
. Тогда высота вертикального ножа с учетом вспушенности определяется выражением
![]() , (3)
, (3)
Для солонцов Западного Казахстана мощность гумусового слоя колеблется в пределах 0,06…0,12м, при глубине их обработки 0,30м и принятой величине вспушенности 0,04м, высота вертикальных ножей должна быть 0,28…0,22м. Таким образом, высота ножей определяется из технологических параметров процесса послойной обработки почвы.
Для определения расстояния между ножами представим рабочий орган как двугранный клин, на котором установлены параллельно два вертикальных ножа толщиной ![]() и углом заточки
и углом заточки ![]() (рис. 2). Относительная деформация почвы, находящиеся между двумя вертикальными ножами определяется уравнением
(рис. 2). Относительная деформация почвы, находящиеся между двумя вертикальными ножами определяется уравнением
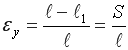 , (4)
, (4)
где ![]() – первоначальная ширина пласта, равная расстоянию между осевыми линиями соседних ножей, м;
– первоначальная ширина пласта, равная расстоянию между осевыми линиями соседних ножей, м;
![]() – ширина пласта после деформаций, равная расстоянию между внутренними боковыми поверхностями соседних ножей, м.
– ширина пласта после деформаций, равная расстоянию между внутренними боковыми поверхностями соседних ножей, м.
Для определения ![]() рассмотрим элементарный объем почвы, находящейся между ножами под действием главных напряжений
рассмотрим элементарный объем почвы, находящейся между ножами под действием главных напряжений ![]() . В связи с тем
. В связи с тем ![]() , то относительная деформация вдоль оси
, то относительная деформация вдоль оси ![]() на основании обобщенного закона Гука равна
на основании обобщенного закона Гука равна
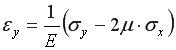 , (5)
, (5)
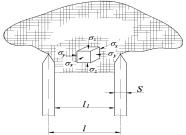
Рис. 2. Схема к обоснованию расстояния между вертикальными ножами
При достижении критической величины деформации ![]() происходит разрушения пласта. Зависимость изменения расстояния между ножами от критической величины относительной деформации почвы приведена на рисунке 3. Из графика видно, что расстояния между ножами зависит от их толщины, физико-механических свойств почвы (модули деформации
происходит разрушения пласта. Зависимость изменения расстояния между ножами от критической величины относительной деформации почвы приведена на рисунке 3. Из графика видно, что расстояния между ножами зависит от их толщины, физико-механических свойств почвы (модули деформации ![]() и сдвига
и сдвига ![]() , коэффициент Пуассона
, коэффициент Пуассона ![]() ).
).
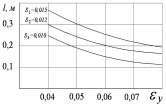
Рис. 3. Зависимость расстояния между вертикальными ножами от величины критической относительной деформации почвы
В. А. Баладинский рекомендует для тяжелых глинистых почв, какими являются солонцы, принимать значение ![]() [3, с. 84]. Тогда расстояние между ножами должны быть 0,17…0,25м при толщине ножей 0,01…0,015м.
[3, с. 84]. Тогда расстояние между ножами должны быть 0,17…0,25м при толщине ножей 0,01…0,015м.
Окончательный выбор расстояния между ножами требует экспериментального определения физико-механических свойств почвы ![]() ,
,![]() ,
, ![]() .
.
Углы заточки и установки ко дну борозды вертикального ножа влияют на его тяговое сопротивление. Для обоснования угла заточки рассмотрим процесс взаимодействия ножа с солонцовым горизонтом с позиции контактной задачи теории упругости. При этом допустим, что почва линейно-деформируемая среда до пределов ее разрушения [4, с.11].
В реальных условиях работы лезвия ножа быстро приобретают форму закругленной поверхности [5, с.27]. Поэтому форму режущей части ножа примем в виде клина с закругленной вершиной радиусом ![]() мм, почву в виде упругой полуплоскости (рис.4).
мм, почву в виде упругой полуплоскости (рис.4).
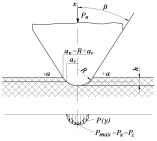
Рис. 4. Схема взаимодействия клина с почвой
Вершина клина является частью цилиндра – сегмента. Поэтому распределение давления в зоне контакта закругленного клина с почвой выражается уравнением [6, с.58]
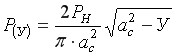 , (6)
, (6)
где ![]() – усилие воздействия ножа на почву, кН;
– усилие воздействия ножа на почву, кН;
![]() – полуширина участка контакта, м;
– полуширина участка контакта, м;
![]() – координата точки, в которой определяется давление, м.
– координата точки, в которой определяется давление, м.
Полуширина участка контакта закругленной части клина с почвой определяется выражением
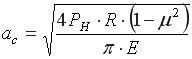 (7)
(7)
Отсюда определяем усилие воздействия ножа на почву
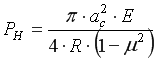 (8)
(8)
При внедрении ножа в почву на глубину, равную высоте сегмента ![]() , т.е. до точки перехода закругленной части в клин, полуширина контакта сегмента с почвой
, т.е. до точки перехода закругленной части в клин, полуширина контакта сегмента с почвой ![]() будет равна полуширина контакта клина с почвой
будет равна полуширина контакта клина с почвой ![]() или радиусу
или радиусу![]() закругления,
закругления, ![]()
Давление в средней части ножа при ![]() ,
, ![]() (рис. 4). Максимальное давление равно
(рис. 4). Максимальное давление равно
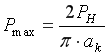 (9)
(9)
Тогда усилие внедрения ножа в почву
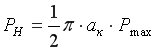 (10)
(10)
Полуширина контакта клина с почвой, выраженная через параметры клина
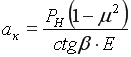 , (11)
, (11)
где ![]() – половина угла заточки ножа, м.
– половина угла заточки ножа, м.
Совестно решая формулы (9), (10) и (11), определяем половину угла заточки ножа без учета трения почвы
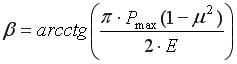 (12)
(12)
С учетом физико-механических свойств почвы, формула примет вид
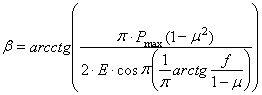 , (13)
, (13)
где ![]() – коэффициент трения почвы о сталь.
– коэффициент трения почвы о сталь.
Построим графические зависимости угла заточки ножа ![]() от коэффициента Пуассона
от коэффициента Пуассона ![]() (рис. 5) и влажности
(рис. 5) и влажности ![]() солонцового слоя (рис.6), используя значения коэффициента внешнего трения солонцов по Ю. А. Тагину.
солонцового слоя (рис.6), используя значения коэффициента внешнего трения солонцов по Ю. А. Тагину.
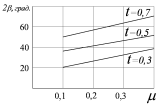
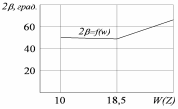
Рис. 5. Влияние коэффициента Пуассона ![]() и влажности
и влажности ![]() солонцового слоя на угол заточки вертикальных ножей
солонцового слоя на угол заточки вертикальных ножей
Величина угла заточки ножа с увеличением коэффициента Пуассона и коэффициента внешнего трения возрастает. С увеличением влажности почвы до 19% угол заточки остается постоянным, а затем возрастает. Оптимальная влажность для солонцов 18…25%, при которой почва хорошо крошится и расходуется на ее обработку минимальное количество энергии [7, с.16]. Этой влажности почвы соответствует теоретический оптимальный угол заточки ![]() (рис. 5), который близок к экспериментальному значению угла заточки ножа для глинистых почв [8, с. 49].
(рис. 5), который близок к экспериментальному значению угла заточки ножа для глинистых почв [8, с. 49].
Таким образом, полученная зависимость позволяет определить оптимальный угол заточки ножа с учетом региональных особенностей почв.
Сила сопротивления резанию вертикальным ножом зависит не только от угла его заточки, но и от угла наклона его ко дну борозды [9, с.73]. Наименьшая энергоемкость технологического процесса соответствует к резанию со скольжением. Для определения угла наклона ножа ко дну борозды рассмотрим его воздействие на почву и укажем все составляющие результирующей силы ![]() (рис. 6).
(рис. 6).
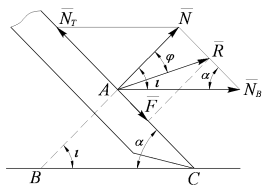
Рис. 6. Схема к определению угла - установки вертикальных ножей ко дну борозды
Почва будет перемещаться по ножу, если касательная составляющая нормальной силы ![]() будет больше, чем максимальная сила трения
будет больше, чем максимальная сила трения ![]() почвы о его поверхность
почвы о его поверхность ![]() . Если учесть, что
. Если учесть, что 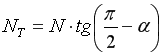 ,
, ![]() , то условие скольжения можно записать в следующем вид
, то условие скольжения можно записать в следующем вид
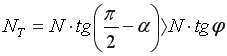 , (14)
, (14)
где ![]() – нормальная сила, кН;
– нормальная сила, кН;
![]() – угол наклона ножа ко дну борозды, град;
– угол наклона ножа ко дну борозды, град;
![]() – угол трения, град.
– угол трения, град.
Это условие выполняется при неравенстве 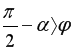 . При оптимальной влажности солонцового горизонта
. При оптимальной влажности солонцового горизонта ![]() угол трения имеет значение
угол трения имеет значение ![]() . Тогда угол наклона ножей должен быть
. Тогда угол наклона ножей должен быть ![]() . Это обеспечивает резание со скольжением и приведет к снижению энергоемкости рабочего органа. Однако в этом случае возникает возможность перемещения солонцового горизонта на поверхность поля, что нельзя по агротехническим требованиям. Поэтому устанавливать ножи ко дну борозды под углом меньше 530 нерационально.
. Это обеспечивает резание со скольжением и приведет к снижению энергоемкости рабочего органа. Однако в этом случае возникает возможность перемещения солонцового горизонта на поверхность поля, что нельзя по агротехническим требованиям. Поэтому устанавливать ножи ко дну борозды под углом меньше 530 нерационально.
Литература:
- Нуралин Б. Н., Обоснование схемы комбинированного рыхлителя для мелиоративной обработки солонцов/ Б. Н. Нуралин, И. Я. Штейнерт, Д. В. Сакара// Журнал «Уральские нивы». – Свердловск, 1985, №10. – С.58.
- Нуралин Б. Н., Совершенствование конструкции плоскорежущей лапы для почвозащитной и влагосберегающей технологий обработки почвы/ Б. Н. Нуралин, Н. А. Кантарбаев // Научно-практический журнал ЗКАТУ им. Жангир хана «Наука и образование». – Уральск, 2013, №4. – С.112-117.
- Баладинский В. А., Динамическое разрушение грунтов / В. А. Баландинский. – Киев, КГУ, 1973. – 243с.
- 4. Бабицский Л. Ф., Исследование и обоснование геометрических параметров зубчатого рабочего органа культиваторов для противоэрозионной обработки почвы/ Л. Ф. Бабицский// Автореф. дис. … канд. техн. наук. – Челябинск,1979. – 20 с.
- Цитович Н. А., Механика грунтов. –М.: Высшая школа 1983. – 288с.
- Штайерман И. Я., Контактная задача теории упругости / И. Я. Штайерман. – М.: Госиздат, 1949. – 270с.
- Тагин Ю. А., Исследование технологических свойств солонцовых почв Барабинской низменности в целях обоснований рациональной технологии их обработки/ Ю. А. Тагин // Автореф. дис. … канд. техн. наук. – Омск, 1970. – 28с.
- Далин А. Д., Ротационные землеройные и грунтообрабатывающие машины / А. Д. Далин, П. В. Павлов. – М.:Машгиз, 1950. – 250с.
- Зеленин А. Н., Основы разрушения грунтов механическими способами / А.Н. Зеленин. – М., 1968. – 372с.

