Определение наилучших вероятностей мутации генетического алгоритма в сетях с двухфазной маршрутизацией
Авторы: Сапрыкин Алексей Николаевич, Гончарова Дарья Игоревна, Малютина Екатерина Витальевна
Рубрика: 3. Автоматика и вычислительная техника
Опубликовано в
III международная научная конференция «Технические науки в России и за рубежом» (Москва, июль 2014)
Дата публикации: 03.07.2014
Статья просмотрена: 238 раз
Библиографическое описание:
Сапрыкин, А. Н. Определение наилучших вероятностей мутации генетического алгоритма в сетях с двухфазной маршрутизацией / А. Н. Сапрыкин, Д. И. Гончарова, Е. В. Малютина. — Текст : непосредственный // Технические науки в России и за рубежом : материалы III Междунар. науч. конф. (г. Москва, июль 2014 г.). — Т. 0. — Москва : Буки-Веди, 2014. — С. 54-57. — URL: https://moluch.ru/conf/tech/archive/90/5946/ (дата обращения: 27.04.2024).
Рассматривается влияние степени мутации генетического алгоритма на его производительность, вычисляется оптимальное значение параметров мутации для хромосом в условиях использования генетического алгоритма в сетях с двухфазной маршрутизацией.
Ключевые слова: сети с двухфазной маршрутизацией, программно определяемые сети, технология открытых потоков, генетические алгоритмы, мутация.
На данный момент компьютерные сети стали неотъемлемой частью инфраструктуры современного мира. Важным показателем для них является простота настройки и программирования с учетом нужд индивидуальных пользователей. Технология открытых потоков OpenFlow позволяет применять в обычных телекоммуникационных сетях инновационные протоколы маршрутизации и коммутации. С одной стороны, возможность применения OpenFlow полностью реализует свой потенциал в области экспериментальных исследований гетерогенных маршрутизаторов сетей с высокой плотностью портов.
С другой стороны, перспективным является применение технологии открытых потоков при многопотоковой маршрутизации, в условиях которой она является наиболее эффективным решением. В работах [1, 2] предлагается инновационный подход, который подразумевает одновременное использование технологии открытых потоков в сетях с двухфазной многопотоковой маршрутизацией.
Основой данного подхода является нахождение распределений времени передачи пакетов в сети с двухфазной маршрутизацией для контроля параметра качества сети — вариации времени передачи пакетов. Агрегирования потоков происходит на двух уровнях — на уровне базового канала в пределах одной фазы сети и на уровне двух путей между узлами двухфазной сети.
Использование генетического алгоритма для оптимизации информационных потоков в рассмотренных сетях обусловлено неэффективностью применения стандартных методов поиска в силу большого количества комбинаций исходных данных. В сети с двухфазной маршрутизацией, состоящей из 32 узлов, передается 10 потоков. Каждый из них распределяется между двумя трактами передачи, а соотношение между частями потока определяется произвольно. В таком случае число возможных комбинаций распределения потоков можно вычислить по формуле:
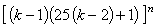 , (1)
, (1)
где k обозначает число узлов в сети, а n — количество потоков. Тогда число неповторяющихся комбинаций распределения потоков составит 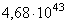 .
.
Одним из наиболее важных параметров генетического алгоритма является вероятность мутации. Слишком большое значение вероятности мутации может привести к слишком быстрой смены потомков без использования их полного потенциала, в то время как правильная настройка данного параметра позволит быстрее и точнее решать поставленные задачи.
Существуют различные подходы к определению вероятности мутации 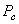 [3, 4]. Как правило, значение
[3, 4]. Как правило, значение 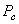 колеблется в пределах 0.5 ~ 1.0. Однако приведенные значения не могут быть генерализированы вследствие того, что они были рассмотрены для решения частных проблем. Все это обуславливает необходимость индивидуального подбора значения вероятности мутации в каждом отдельно взятом случае.
колеблется в пределах 0.5 ~ 1.0. Однако приведенные значения не могут быть генерализированы вследствие того, что они были рассмотрены для решения частных проблем. Все это обуславливает необходимость индивидуального подбора значения вероятности мутации в каждом отдельно взятом случае.
Для определения влияния изменения уровня мутации представим ряд тестов, которые должны выявить наилучшие значения процента мутации. Поиск особей с наилучшими значениями функции полезности производится по следующему алгоритму:
Шаг 1. Запуск алгоритма. Создание начальной популяции
Шаг 2. Определение функции полезности особей.
Шаг 3. Достигнуто ли необходимое значение функции полезности? Если да, то переходим к шагу 5. Иначе переходим к шагу 4.
Шаг 4. Новый отбор. Скрещивание и мутации особей. Создание новой популяции. Переход к шагу 2.
Шаг 5. Выбор наилучшей особи. Конец поиска.
В соответствии с данным алгоритмом каждая особь ранжируется в зависимости от значения функции полезности. Целью оптимизации всей сети считаем сведение к минимуму 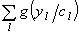 при предельно допустимых значениях средней задержки передачи потока и ее вариации в пути l, где l — порядковый номер линии сети,
при предельно допустимых значениях средней задержки передачи потока и ее вариации в пути l, где l — порядковый номер линии сети, 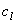 — фиксированная предельная скорость передачи данных по линии l.
— фиксированная предельная скорость передачи данных по линии l. 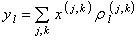 — объем трафика по каждой линии, где
— объем трафика по каждой линии, где 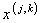 – скорость трафика, входящего в маршрутизатор j, который предназначен маршрутизатору k. Штрафная функция g является выпуклой, неубывающей и дважды дифференцируемой функцией, которая налагает штраф при увеличении нагрузки линии. В качестве штрафной функции выбирается экспоненциальная функция.
– скорость трафика, входящего в маршрутизатор j, который предназначен маршрутизатору k. Штрафная функция g является выпуклой, неубывающей и дважды дифференцируемой функцией, которая налагает штраф при увеличении нагрузки линии. В качестве штрафной функции выбирается экспоненциальная функция.
В результате проведенного исследования, были проведены симуляции нескольких тестовых сценариев. Эксперименты проводились на компьютере со следующими характеристиками: Intel Core i7 2,0 GHz, RAM 8Gb.
Используемые в экспериментах параметры генетического алгоритма были установлены следующим образом: размер популяции — 40 особей, вероятность скрещивания — 0.8, число поколений — 100. Процент мутации варьировался от 0.01 до 0.5, причем для каждой отдельно взятой серии экспериментов вероятность мутации оставалась постоянной. Таким образом были использованы 10 возможных значений вероятности мутации: 0.01/0.03/0.05/0.07/0.1/0.15/0.2/0.3/0.4/0.5. Были рассмотрены сети с двухфазной маршрутизацией, состоящие из 8, 16 и 32 узлов. Вследствие стохастического характера генетических алгоритмов для каждого варианта было проведено 30 экспериментов.
Таблица 1
Значения функции полезности для различных значений вероятности мутации в сетях с двухфазной маршрутизацией из 8 узлов
|
Вероятность мута-ции |
Функция полезности, условные единицы |
||
|
Сеть из 8 узлов |
|||
|
Средний результат |
Лучший результат |
Худший результат |
|
|
0,01 |
339,1 |
285 |
409 |
|
0,03 |
275,5 |
243 |
313 |
|
0,05 |
272,4 |
243 |
320 |
|
0,07 |
270,6 |
221 |
350 |
|
0,1 |
268,9 |
245 |
306 |
|
0,15 |
280,2 |
247 |
325 |
|
0,2 |
299,8 |
263 |
325 |
|
0,3 |
305,9 |
263 |
370 |
|
0,4 |
322,6 |
267 |
380 |
|
0,5 |
337,8 |
288 |
415 |
|
0,01 |
339,1 |
285 |
409 |
|
0,03 |
275,5 |
243 |
313 |
|
0,05 |
272,4 |
243 |
320 |
Таблица 2
Значения функции полезности для различных значений вероятности мутации в сетях с двухфазной маршрутизацией из 16 и 32 узлов
|
Вероятность мута-ции |
Функция полезности, условные единицы |
Функция полезности, условные единицы |
||||
|
Сеть из 16 узлов |
Сеть из 32 узлов |
|||||
|
Средний результат |
Лучший результат |
Худший результат |
Средний результат |
Лучший результат |
Худший результат |
|
|
0,01 |
626,9 |
542 |
726 |
1435,8 |
1323 |
1549 |
|
0,03 |
535,5 |
479 |
592 |
1438,9 |
1278 |
1530 |
|
0,05 |
534,2 |
505 |
572 |
1477,4 |
1372 |
1622 |
|
0,07 |
544,4 |
515 |
594 |
1487,2 |
1416 |
1559 |
|
0,1 |
551,3 |
501 |
582 |
1532 |
1401 |
1683 |
|
0,15 |
598,1 |
547 |
726 |
1567,8 |
1464 |
1660 |
|
0,2 |
620,9 |
579 |
681 |
1669,9 |
1585 |
1789 |
|
0,3 |
625,9 |
574 |
696 |
1738,6 |
1561 |
1908 |
|
0,4 |
663,9 |
625 |
737 |
1686,7 |
1530 |
1881 |
|
0,5 |
730,6 |
643 |
834 |
1722,8 |
1605 |
1850 |
В таблицах 1 и 2 содержатся средние, лучшие и худшие результаты функции полезности для различных значений вероятности мутации.
Эксперименты показали, что увеличение процента мутации с 0.05 до 0.5 значительно ухудшает средние результаты функции полезности. Однако, следует учитывать, что дальнейшее уменьшение процента мутации оказывает негативное влияние на значение функции полезности.
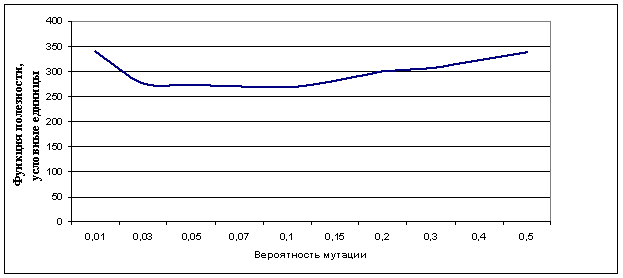
Рис. 1. Средние значения функции полезности, полученные за 30 экспериментов для различных значений вероятности мутации для сети с двухфазной маршрутизацией из 8 узлов
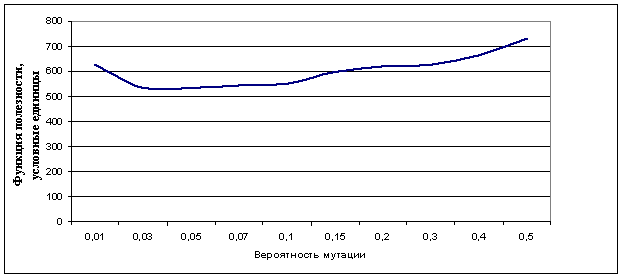
Рис. 2. Средние значения функции полезности, полученные за 30 экспериментов для различных значений вероятности мутации для сети с двухфазной маршрутизацией из 16 узлов
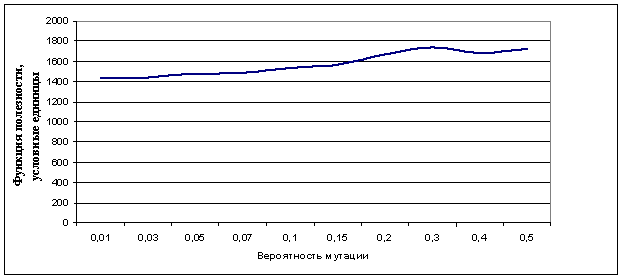
Рис. 3. Средние значения функции полезности, полученные за 30 экспериментов для различных значений вероятности мутации для сети с двухфазной маршрутизацией из 32 узлов
Для лучшей интерпретации полученные числовые результаты были визуализированы в рис. 1–3. Графические результаты показывают, что оптимальное значение мутации колеблется в рамках от 5 до 10 процентов для сетей с двухфазной маршрутизацией, состоящих не более чем из 32 узлов. Отклонение от этих показателей в большую или меньшую сторону приводит к ухудшению результатов. Таким образом, правильный выбор значения вероятности мутации генетического алгоритма значительно улучшает его точность.
Литература:
1. Ижванов Ю. Л., Корячко В. П., Шибанов А. П., Сапрыкин А. Н., Лукьянов О. В. Оптимизация сети с дозированной балансировкой нагрузки // Научно-технический журнал «Системы управления и информационные технологии». Москва-Воронеж, 2012. № 3(49). С. 37–42.
2. Корячко В. П., Шибанов А. П., Сапрыкин А. Н. Расчет вариации времени передачи пакетов в сети с двухфазной маршрутизацией [Электронный ресурс]: Труды XII всероссийского совещания по проблемам управления. — Электрон, дан. — М.: ИПУ РАН, сор. 2014. — 1 электрон, опт. диск (CD-ROM): зв., цв.12 см. — Систем. требования: ПК с процессором 486 DX2–66; 8 Мб ОЗУ; Microsof Windows 3.1 или Windows 95; 2-скоростной дисковод CD-ROM; видеокарта SVGA 256 цв.; зв. карта 16 бит стандарта МРС; стереоколонки или наушники. — Загл. с этикетки диска.
3. Bäck T., “Optimal mutation rates in genetic search,” in Proceedings of the Fifth International Conference on Genetic Algorithms, 1993, pp. 2–8.
4. Hesser J. and Männer R., “Towards on optimal mutation probability for genetic algorithms,” in Proceedings of Parallel Problem Solving from Nature Conference, 1990, pp. 23–32.
Ключевые слова
генетические алгоритмы, мутация, сети с двухфазной маршрутизацией, программно определяемые сети, технология от-крытых потоковПохожие статьи
Применение генетического алгоритма для решения задачи...
двухфазная маршрутизация, значение функции полезности, сеть, различное значение вероятности мутации, генетический алгоритм, узел, функция полезности...
Подход к систематическому выбору и обоснованию алгоритмов
Определение наилучших вероятностей мутации генетического алгоритма в сетях с двухфазной маршрутизацией. Анализ эффективности алгоритмов сортировки и вcтроенных...
Определение наилучших вероятностей мутации генетического...
Методом наименьших квадратов были получены линейные уравнения регрессии для магистрали и. Определение наилучших вероятностей мутации генетического алгоритма в сетях с двухфазной маршрутизацией.
Анализ мер риска, построенных на основе ассиметричных...
Функция полезности Бернулли основана на объективном уровне благосостояния индивида и рассматривает только положительные значения, тогда как функция полезности Канемана-Тверски основывается на субъективно определенной точке отсчета...
С++ библиотека компонентов генетических алгоритмов
В данном классе содержатся все необходимые методы для реализации генетических алгоритмов. Такими методами являются инициализация популяции, установка и извлечение функций кроссинговера и мутации, установка и извлечение функций выборки...
Определение наилучших вероятностей мутации генетического...
Библиографическое описание: Сапрыкин А. Н., Гончарова Д. И., Малютина Е. В. Определение наилучших вероятностей мутации генетического алгоритма в сетях с двухфазной маршрутизацией [Текст] // Технические науки в России и за рубежом: материалы III Междунар...
Надежность ПЦР-анализа при обнаружении m.tuberculosis...
Надежность ПЦР-анализа при обнаружении m.tuberculosis и мутации гена rpoB при исследовании различного диагностического материала.
MTB, RIF, молекулярно-генетический метод, отрицательный результат, прогностическая ценность, лекарственная устойчивость...
Обзор методов решения задачи удовлетворения ограничений
Следующим шагом «скрещиваем лучших особей» и формируем новое «поколение», заменяя худшие решения.
Важно отметить, что на определенном этапе решение может зациклиться, для исключения зацикливания генетический алгоритм предусматривает «мутации».
Статьи по ключевому слову "мутация" — Молодой учёный
"мутация": Молодой учёный №1 (105) январь-1 2016 г. — Елмуратова С. А.
Определение наилучших вероятностей мутации генетического алгоритма в сетях с двухфазной маршрутизацией.
Похожие статьи
Применение генетического алгоритма для решения задачи...
двухфазная маршрутизация, значение функции полезности, сеть, различное значение вероятности мутации, генетический алгоритм, узел, функция полезности...
Подход к систематическому выбору и обоснованию алгоритмов
Определение наилучших вероятностей мутации генетического алгоритма в сетях с двухфазной маршрутизацией. Анализ эффективности алгоритмов сортировки и вcтроенных...
Определение наилучших вероятностей мутации генетического...
Методом наименьших квадратов были получены линейные уравнения регрессии для магистрали и. Определение наилучших вероятностей мутации генетического алгоритма в сетях с двухфазной маршрутизацией.
Анализ мер риска, построенных на основе ассиметричных...
Функция полезности Бернулли основана на объективном уровне благосостояния индивида и рассматривает только положительные значения, тогда как функция полезности Канемана-Тверски основывается на субъективно определенной точке отсчета...
С++ библиотека компонентов генетических алгоритмов
В данном классе содержатся все необходимые методы для реализации генетических алгоритмов. Такими методами являются инициализация популяции, установка и извлечение функций кроссинговера и мутации, установка и извлечение функций выборки...
Определение наилучших вероятностей мутации генетического...
Библиографическое описание: Сапрыкин А. Н., Гончарова Д. И., Малютина Е. В. Определение наилучших вероятностей мутации генетического алгоритма в сетях с двухфазной маршрутизацией [Текст] // Технические науки в России и за рубежом: материалы III Междунар...
Надежность ПЦР-анализа при обнаружении m.tuberculosis...
Надежность ПЦР-анализа при обнаружении m.tuberculosis и мутации гена rpoB при исследовании различного диагностического материала.
MTB, RIF, молекулярно-генетический метод, отрицательный результат, прогностическая ценность, лекарственная устойчивость...
Обзор методов решения задачи удовлетворения ограничений
Следующим шагом «скрещиваем лучших особей» и формируем новое «поколение», заменяя худшие решения.
Важно отметить, что на определенном этапе решение может зациклиться, для исключения зацикливания генетический алгоритм предусматривает «мутации».
Статьи по ключевому слову "мутация" — Молодой учёный
"мутация": Молодой учёный №1 (105) январь-1 2016 г. — Елмуратова С. А.
Определение наилучших вероятностей мутации генетического алгоритма в сетях с двухфазной маршрутизацией.











