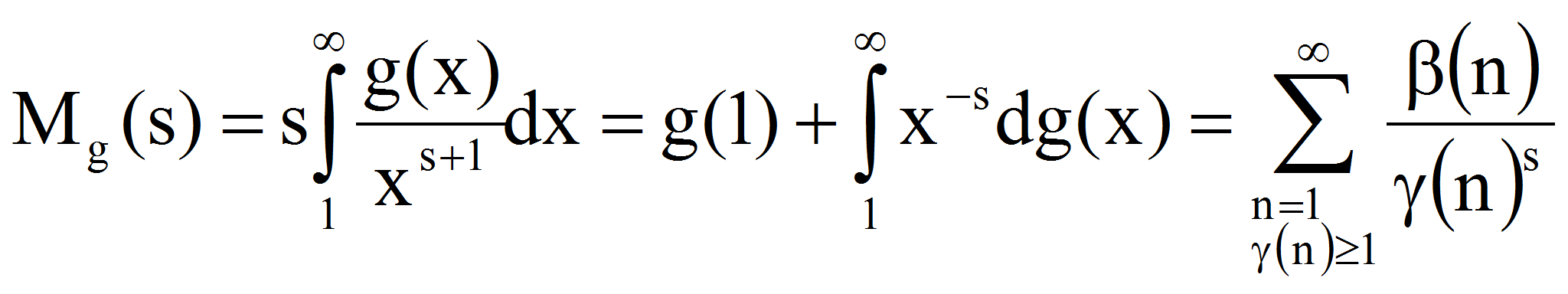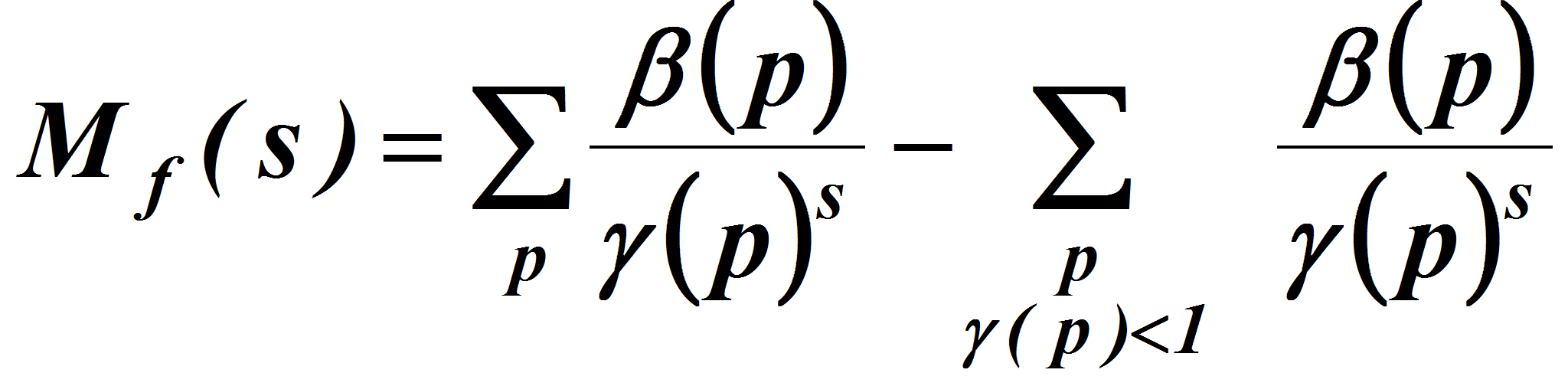О некоторых задачах теории мультипликативных функций
Автор: Оразов Мамед
Рубрика: 14. Общие вопросы технических наук
Опубликовано в
международная научная конференция «Современные тенденции технических наук» (Уфа, октябрь 2011)
Статья просмотрена: 31 раз
Библиографическое описание:
Оразов, Мамед. О некоторых задачах теории мультипликативных функций / Мамед Оразов. — Текст : непосредственный // Современные тенденции технических наук : материалы I Междунар. науч. конф. (г. Уфа, октябрь 2011 г.). — Уфа : Лето, 2011. — С. 73-75. — URL: https://moluch.ru/conf/tech/archive/5/957/ (дата обращения: 27.04.2024).
Работа посвящена задачам, где изучается асимптотическое поведение суммы значений мультипликативных функций. Устанавливается связь между такими суммами по простым числам и натуральным числам. Результаты, полученные в работе, основаны на исследовании аналитических свойств указанных сумм и имеют приложения в теории свободных нормированных полугрупп.
Work is devoted problems where it is studied асимптотическое behavior of the sum of values of multiplicative functions. Connection between such sums on simple numbers and natural numbers is established. The results received in work, are based on research of analytical properties of the specified sums and have appendices in the theory free normative semi groups.
Пусть
![]() и
и
![]() − неотрицательные мультипликативные функции. Определим функции
− неотрицательные мультипликативные функции. Определим функции
![]() и
и
![]() следующим образом:
следующим образом:
(![]() −простые числа,
−простые числа,
![]() −
натуральные числа). Введем обозначения;
−
натуральные числа). Введем обозначения;
![]()
![]()
Учитывая определения функции
![]() и
и
![]() ,
имеем
,
имеем
Предположим, что ряд
![]() сходится в полуплоскости
сходится в полуплоскости
![]() .
.
Начиная с этого момента, мы предполагаем также, что
![]() для всех натуральных
для всех натуральных
![]() .
Так как все члены ряда
.
Так как все члены ряда
неотрицательные числа, то отсюда следует, что ряд
для
![]()
(а следовательно и ряд для
![]() )
при
)
при
![]() сходится абсолютно. Доказывается следующие теоремы:
сходится абсолютно. Доказывается следующие теоремы:
Теорема 1. Пусть
![]() и
и
![]() −
неотрицательные мультипликативные функции, причем
−
неотрицательные мультипликативные функции, причем
![]() для всех
для всех
![]() .
.
Тогда если ряды
Рассмотрим несколько следствий теоремы 1.
Следствие 1. Пусть
![]() &#;
неотрицательная мультипликативная функция
&#;
неотрицательная мультипликативная функция
![]() ,
,
![]() ,
,
![]() .
.
то
В частности, этим условиям удовлетворяет функция
![]() .
Поэтому отсюда следует закон простых чисел.
.
Поэтому отсюда следует закон простых чисел.
Следствие 2. Пусть
![]() &#;
мультипликативная функция,
&#;
мультипликативная функция,
![]() для всех неотрицательных
для всех неотрицательных
![]() .
.
Тогда если ряды
сходятся и
то
Теорема 2. Пусть
![]() и
и
![]() −
неотрицательные, вполне мультипликативные функции,
−
неотрицательные, вполне мультипликативные функции,
![]() при всех простых
при всех простых
![]() .
.
Тогда если ряд
сходится, то
Теорема 3. Пусть
![]() и
и
![]() −
неотрицательные мультипликативные функции,
−
неотрицательные мультипликативные функции,
![]() для всех простых
для всех простых
![]() и выполнено условие (1).
и выполнено условие (1).
Тогда
- Литература:
Файнлейб А.С. Некоторые асимптотические формулы для сумм мультипликативных функций и их приложения.&#; Литовский матем. сборник, 7, №13, 1967, 535-545.
Ингам А.Е. Распределение простых чисел.&#; ОНТИ, 1936.
Титчмарш Е.К. Теория дзета-функции Римана.&#; ИЛ, 1953.
Похожие статьи
Функции Бесселя и их свойства | Статья в журнале...
где — произвольное вещественное число (в общем случае комплексное), называемое порядком. Функцию Бесселя индекса можно определить рядом
Функцию Бесселя индекса можно определить рядом
Основные термины (генерируются автоматически): функция, ряд, число.
, где - функция от ряда переменных, в том числе от .
Функции Бесселя | Статья в журнале «Молодой ученый»
где — произвольноевещественное число(в общем случае комплексное), называемоепорядком. Функцию Бесселя индекса можно определить рядом
Метод суммирования расходящихся рядов путем сведения...
Доказательство: Сначала следует доказать, что ряд: , имеет обобщенной суммой число .
Вычислив погрешность кубатурной формулы (3) для этой функции, получим следующее...
Роль больших простых чисел в современной криптографии
Последовательный выбор чисел требует больше времени, также использование ряда выбранных простых чисел
Эта функция существует во многих языках программирования.
Функцию Бесселя индекса можно определить рядом: где...
Классическая постановка задачи о распределении простых чисел в натуральном ряду состоит в исследовании асимптотического поведения функции означающий число простых чисел...
Разработка способа представления длинных чисел в памяти...
Наиболее мощные калькуляторы, реализующие длинную арифметику, имеют ряд недостатков
Все функции для записи числа и выполнения расчетов вынесены в библиотеку...
Методика определения функций принадлежности для...
Алгоритм интервального оценивания параметров нелинейных... m — число параметров функции-модели; n — число точек регрессии.
Особенности вычисления временных интервалов в Excel
Если заданное число месяцев принять равным нулю, то функция возвратит дату последнего дня текущего месяца.
Похожие статьи
Функции Бесселя и их свойства | Статья в журнале...
где — произвольное вещественное число (в общем случае комплексное), называемое порядком. Функцию Бесселя индекса можно определить рядом
Функцию Бесселя индекса можно определить рядом
Основные термины (генерируются автоматически): функция, ряд, число.
, где - функция от ряда переменных, в том числе от .
Функции Бесселя | Статья в журнале «Молодой ученый»
где — произвольноевещественное число(в общем случае комплексное), называемоепорядком. Функцию Бесселя индекса можно определить рядом
Метод суммирования расходящихся рядов путем сведения...
Доказательство: Сначала следует доказать, что ряд: , имеет обобщенной суммой число .
Вычислив погрешность кубатурной формулы (3) для этой функции, получим следующее...
Роль больших простых чисел в современной криптографии
Последовательный выбор чисел требует больше времени, также использование ряда выбранных простых чисел
Эта функция существует во многих языках программирования.
Функцию Бесселя индекса можно определить рядом: где...
Классическая постановка задачи о распределении простых чисел в натуральном ряду состоит в исследовании асимптотического поведения функции означающий число простых чисел...
Разработка способа представления длинных чисел в памяти...
Наиболее мощные калькуляторы, реализующие длинную арифметику, имеют ряд недостатков
Все функции для записи числа и выполнения расчетов вынесены в библиотеку...
Методика определения функций принадлежности для...
Алгоритм интервального оценивания параметров нелинейных... m — число параметров функции-модели; n — число точек регрессии.
Особенности вычисления временных интервалов в Excel
Если заданное число месяцев принять равным нулю, то функция возвратит дату последнего дня текущего месяца.