Исследование нелинейной системы «Преобразователь частоты – асинхронный двигатель»
Автор: Касымова Айнур Есбергеновна
Рубрика: 5. Энергетика
Опубликовано в
III международная научная конференция «Технические науки: теория и практика» (Чита, апрель 2016)
Дата публикации: 31.03.2016
Статья просмотрена: 963 раза
Библиографическое описание:
Касымова, А. Е. Исследование нелинейной системы «Преобразователь частоты – асинхронный двигатель» / А. Е. Касымова. — Текст : непосредственный // Технические науки: теория и практика : материалы III Междунар. науч. конф. (г. Чита, апрель 2016 г.). — Чита : Издательство Молодой ученый, 2016. — С. 72-77. — URL: https://moluch.ru/conf/tech/archive/165/9973/ (дата обращения: 26.04.2024).
В статье рассматриваются замкнутая система ПЧ-АД с корректирующим нелинейным звеном. Дается математическая модель динамики переходных процессов скорости электромагнитного момента асинхронного двигателя. Приведена программа расчета оптимального управления на алгоритмическом языке MATLAB.
Ключевые слова: корректирующее звено, математическая модель, переходные процессы, асинхронный двигатель.
In article are considered the closed system of PCh-AD with the correcting nonlinear link. The mathematical model of dynamics of transition processes of speed of the electromagnetic moment of the asynchronous engine is given. The program of calculation of optimum control is given in algorithmic language of MATLAB.
Keywords: the correcting link, mathematical model, transition processes, the asynchronous engine.
Формирование плавно протекающих переходных процессов в электроприводе переменного тока с короткозамкнутым асинхронным двигателем является одной из основных задач уменьшения больших электромагнитных моментов двигателя, особенно в режиме его пуска [1]. Для осуществления плавно протекающих переходных процессов замкнутой системы преобразователь частоты — асинхронный двигатель (ПЧ-АД) необходимо обеспечить систему задатчиком интенсивности с оптимальным законом управления ![]() , что позволит снизить потери электроэнергии системы ПЧ-АД. Структурная схема нелинейной системы ПЧ-АД в среде MATLAB представлена на рисунке 1.
, что позволит снизить потери электроэнергии системы ПЧ-АД. Структурная схема нелинейной системы ПЧ-АД в среде MATLAB представлена на рисунке 1.
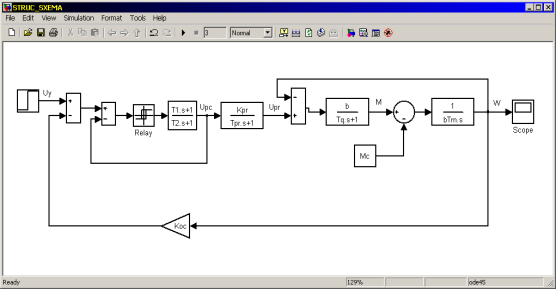
Рис. 1. Структурная схема нелинейной системы ПЧ-АД
Структурная схема нелинейной системы ПЧ-АД создана на основе линеаризованной системы ПЧ-АД с обратной связью по скорости [2]. Как видно из рисунка 1 в структурной схеме замкнутой нелинейной системы ПЧ-АД в регулятор скорости введено идеальное релейное звено, которое обеспечивает желаемые свойства системы [3].
В структурной схеме приняты следующие обозначения [4]: b — модуль жесткости линеаризованной механической характеристики АД; ![]() электромагнитная постоянная времени цепей статора и ротора АД;
электромагнитная постоянная времени цепей статора и ротора АД; ![]() электромеханическая постоянная времени двигателя;
электромеханическая постоянная времени двигателя; ![]() постоянная времени цепи управления преобразователя частоты;
постоянная времени цепи управления преобразователя частоты; ![]() постоянные времени интегро-дифференцирующего звена регулятора скорости;
постоянные времени интегро-дифференцирующего звена регулятора скорости; ![]() передаточный коэффициент преобразователя частоты;
передаточный коэффициент преобразователя частоты; ![]() коэффициент обратной связи по скорости.
коэффициент обратной связи по скорости.
Математическое описание замкнутой системы ПЧ-АД, на основе передаточных функций структурной схемы (рисунок 1), принимает следующий вид:
![]() (1)
(1)
![]() (2)
(2)
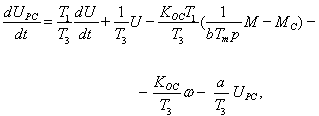 (3)
(3)
где ![]()
![]() угловая скорости вала асинхронного двигателя;
угловая скорости вала асинхронного двигателя; ![]()
![]() электромагнитный момент двигателя;
электромагнитный момент двигателя; ![]() напряжение на выходе регулятора скорости;
напряжение на выходе регулятора скорости; ![]() управление;
управление; ![]() ,
, ![]()
![]() коэффициент гармонической линеаризации статической характеристики идеального релейного звена.
коэффициент гармонической линеаризации статической характеристики идеального релейного звена.
С целью удобства решения задачи оптимального управления замкнутой системой ПЧ-АД преобразуем уравнения (1–3), при ![]() , к следующему виду:
, к следующему виду:
![]() (4)
(4)
![]() (5)
(5)
![]() (6)
(6)
![]() (7)
(7)
здесь ![]()
![]() вспомогательная переменная.
вспомогательная переменная.
Решение задачи оптимального управления осуществляется методом принцип максимума Понтрягина [5, 6]. Критерием оптимальности, в нашем случае, будет минимум функционала:
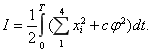 (8)
(8)
Образуем функцию Н, которая будет иметь вид:
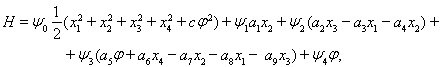 (9)
(9)
где ![]() вспомогательные переменные.
вспомогательные переменные.
Согласно вышеуказанному методу решения задачи оптимального управления, составим следующую систему уравнений:
![]() (10)
(10)
![]() (11)
(11)
![]() (12)
(12)
![]() (13)
(13)
Так как на управление ![]() ограничение не накладывается, то максимум Н (9) определяется из условия
ограничение не накладывается, то максимум Н (9) определяется из условия ![]() :
:
Откуда:
![]() (15)
(15)
Подставляя значение ![]() в систему уравнений (4–7) и объединяя эту систему с уравнениями (10–13), приходим к следующей системе уравнений:
в систему уравнений (4–7) и объединяя эту систему с уравнениями (10–13), приходим к следующей системе уравнений:
![]() (16)
(16)
![]() (17)
(17)
![]() (18)
(18)
![]() (19)
(19)
![]() (20)
(20)
![]() (21)
(21)
![]() (22)
(22)
Граничные условия системы уравнений (6) имеют вид:
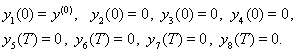 (24)
(24)
Программа решения уравнений (24) приведена на рисунке 2. Программа составлена на основе [7].
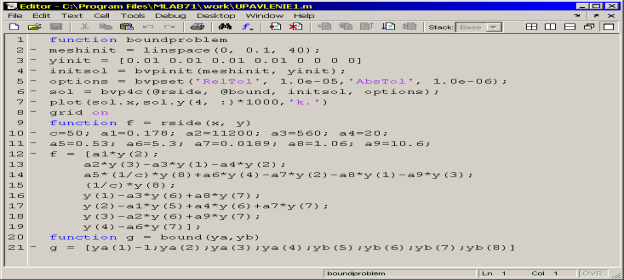
Рис. 2. Программа расчета оптимального управления замкнутой системой «Преобразователь частоты — асинхронный двигатель»
Параметры системы ПЧ-АД рассчитаны для асинхронного двигателя.
Кривая переходного процесса оптимального управления ![]() представлена на рисунке 3.
представлена на рисунке 3.
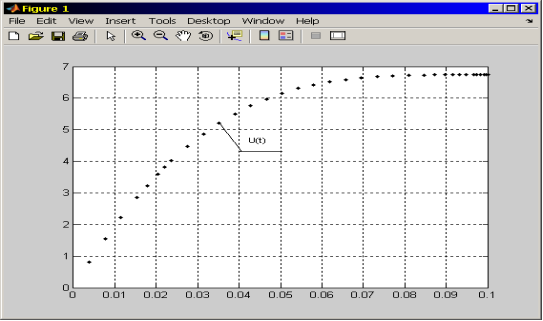
Рис. 3. Кривая переходного процесса оптимального управления замкнутой системой ПЧ-АД
Полученный график переходного процесса оптимального управления дает возможность определить постоянную времени переходного процесса оптимального управления.
Выводы:
- Разработана структурная схема замкнутой релейной системы ПЧ-АД.
- Разработана математическая модель динамики переходных процессов скорости электромагнитного момента асинхронного двигателя.
- Разработана программа расчета оптимального управления замкнутой системой ПЧ-АД.
Литература:
- Браславский И. Я., Ишматов З. Ш., Поляков В. Н. Энергосберегающий асинхронный электропривод. — М.: Издательский центр «Академия», 2004.
- Терехов В. М., Осипов О. И. Системы управления электроприводов. — М.: Издательский центр, «Академия», 2008.
- Попов Е. П. Теория нелинейных систем автоматического регулирования и управления. — М.: Наука, Гл. ред. физ. — мат., лит. 1988.
- Ключев В. И. Теория электропривода. — М.: Энергоатомиздат, 1998.
- Фельдбаум А. А., Бутковский А. Г. Методы автоматического управления. — М.: Издательство «Наука», Гл. ред. физ. — мат., 1971.
- Бесекерский В. А., Попов Е. П. Теория систем автоматического управления. — СПб, Изд — во «Профессия», 2004.
- Ануфриев И. Е., Смирнов А. В., Смирнова Е. Н. MATLAB 7. — СПб.: БХВ, 2005.
Ключевые слова
математическая модель, переходные процессы, асинхронный двигатель, корректирующее звено, асинхронный двигатель.Похожие статьи
Анализ устойчивости замкнутой нелинейной системы...
замкнутая система, MATLAB, асинхронный двигатель, структурная схема, программа расчета, Преобразователь частоты, переходной процесс системы, обратная связь, нелинейное звено, фазовая траектория.
Автоматизация процесса дозирования сыпучего материала...
оптимальное управление, структурная схема, замкнутая система, асинхронный двигатель, MATLAB, переходной процесс, нелинейная система, программа расчета, система уравнений, идеальное релейное звено.
Анализ передаточной функции структурной схемы вентильного...
Структурная схема вентильного двигателя в системе MATLAB представлена на рисунке 1. В линеаризованной структурной схеме вентильного двигателя является угловой скорость частоты вращения вала двигателя.
Моделирование прямого пуска асинхронного двигателя с ШИМ...
4. Нечувствительность системы векторного управления скоростью к изменениям параметров асинхронного двигателя.
В работе Шрейнера в главе 6 «Примеры» дан образец расчета параметров асинхронного двигателя.
Моделирование моментов нагрузки электродвигателей в MATLAB
Моделирование системы векторного управления для привода... MATLAB, Блок, векторное управление, главное движение, модель, переходной процесс напряжений статора, статический момент, короткозамкнутый ротор, асинхронный двигатель, момент времени.
Исследования нелинейного корректирующего устройства...
В статье представлена структурная схема замкнутой системы ПЧ-АД с нелинейным корректирующим устройством. Дается математическое описание динамики замкнутой системы «Преобразователь частоты – асинхронный двигатель»с короткозамкнутым ротором.
Математическое моделирование САР скорости системы...
Рис. 2. Программа расчета оптимального управления замкнутой системой «Преобразователь частоты — асинхронный двигатель». Пространственные векторы в асинхронном двигателе...
Моделирование САР скорости асинхронного двигателя...
уравнение, система координат, структурная схема, роторная система координат, вектор, неподвижная система координат, асинхронный двигатель, электромагнитный момент, неподвижная система координат статора, система...
Математическая модель асинхронного двигателя во...
структурная схема, уравнение, электромагнитный момент, неподвижная система координат, асинхронный двигатель, Проекция уравнения, статорный ток, номинальный режим, математическая модель, система...
Похожие статьи
Анализ устойчивости замкнутой нелинейной системы...
замкнутая система, MATLAB, асинхронный двигатель, структурная схема, программа расчета, Преобразователь частоты, переходной процесс системы, обратная связь, нелинейное звено, фазовая траектория.
Автоматизация процесса дозирования сыпучего материала...
оптимальное управление, структурная схема, замкнутая система, асинхронный двигатель, MATLAB, переходной процесс, нелинейная система, программа расчета, система уравнений, идеальное релейное звено.
Анализ передаточной функции структурной схемы вентильного...
Структурная схема вентильного двигателя в системе MATLAB представлена на рисунке 1. В линеаризованной структурной схеме вентильного двигателя является угловой скорость частоты вращения вала двигателя.
Моделирование прямого пуска асинхронного двигателя с ШИМ...
4. Нечувствительность системы векторного управления скоростью к изменениям параметров асинхронного двигателя.
В работе Шрейнера в главе 6 «Примеры» дан образец расчета параметров асинхронного двигателя.
Моделирование моментов нагрузки электродвигателей в MATLAB
Моделирование системы векторного управления для привода... MATLAB, Блок, векторное управление, главное движение, модель, переходной процесс напряжений статора, статический момент, короткозамкнутый ротор, асинхронный двигатель, момент времени.
Исследования нелинейного корректирующего устройства...
В статье представлена структурная схема замкнутой системы ПЧ-АД с нелинейным корректирующим устройством. Дается математическое описание динамики замкнутой системы «Преобразователь частоты – асинхронный двигатель»с короткозамкнутым ротором.
Математическое моделирование САР скорости системы...
Рис. 2. Программа расчета оптимального управления замкнутой системой «Преобразователь частоты — асинхронный двигатель». Пространственные векторы в асинхронном двигателе...
Моделирование САР скорости асинхронного двигателя...
уравнение, система координат, структурная схема, роторная система координат, вектор, неподвижная система координат, асинхронный двигатель, электромагнитный момент, неподвижная система координат статора, система...
Математическая модель асинхронного двигателя во...
структурная схема, уравнение, электромагнитный момент, неподвижная система координат, асинхронный двигатель, Проекция уравнения, статорный ток, номинальный режим, математическая модель, система...











