Выигрыш преобразования Хартли по коэффициенту ошибок у преобразования Фурье

Сегодня в функциональных узлах цифровой передачи данных широко используется быстрое преобразование Фурье. Интерес к вариантам на основе быстрого преобразования Хартли появился относительно недавно. Обоснованно это тем, что этот метод долгое время находился под защитой патента. В связи с этим обстоятельством разработка эффективных алгоритмов быстрого преобразования Хартли не велась.

Преобразование Хартли — вещественное преобразование, благодаря чему не требуется выполнять операции с мнимой частью. На передающей стороне модуляция происходит с помощью обратного преобразования Хартли, а на приёмной стороне демодуляция — с помощью прямого преобразования Хартли. Так как прямое и обратное преобразования Хартли идентичны, это существенно упрощает аппаратную и программную реализацию многоканальной системы связи, по сравнению с преобразованием Фурье.

Реализация классического способа передачи данных с частотным уплотнением посредством прямого и обратного преобразования Фурье (ПФ) сталкивается с рядом трудностей, среди которых особенно стоит отметить вычислительную сложность, если учесть комплексное представление чисел. Несимметричность ПФ относительно мнимой единицы компенсируется выполнением операции перестановки исходных данных, требующей дополнительных вычислительных затрат.

Альтернативным способом передачи информации по каналу связи является способ, основанный на использовании вещественного преобразования Хартли (ПХ).

Главная идея быстрого вычисления дискретного преобразования Фурье (ДПФ) — вектор делится на части, результаты обработки которых затем сливаются. Разделим общую сумму на две части: первая содержит слагаемые с чётными индексами, вторая — с нечётными. Это равенство даёт способ вычислять k-й коэффициент ДПФ вектора длины N через два преобразования длины N/2, одно из которых применяется к вектору а^чёт из координат вида a_2x, а другое — к вектору a^нечёт из координат вида a_2x+1.

Общая схема алгоритма состоит в повторяющемся сведении ДПФ вектора длины N к векторам длины N/2 и объединении результатов. Базисом рекурсии служат векторы длины 1, для которых ДПФ — сам вектор [1].

Преобразование Хартли. Соотношения прямого и обратного преобразования Хартли записываются в виде пары преобразований:

,

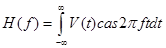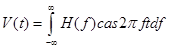
где функция cas представляет собой сумму косинуса и синуса одного и того же аргумента:

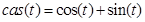
Как видно алгоритм обработки сигналов идентичен как на передающей стороне, так и на приёмной стороне, что существенно упрощает аппаратную и программную реализацию многоканальной системы связи [2].

ДПФ вектора имеет физический смысл, а именно, если вектор представляет собой дискретизированный сигнал, то ДПФ раскладывает его по частотам. Преобразование Хартли не имеет такой явной интерпретации.

Однако, преобразование Хартли можно превратить в преобразование Фурье за N сложений и умножений, что быстрее, чем после обработка в действительные числа.

Поэтому, если исходные данные действительны, то БПХ может быть более эффективным, нежели БПФ. При этом при подстановке представлений коэффициентов Фурье, выраженных через элементы ДПХ, получается весьма удобное для вычислений выражение. Поэтому пересчёта ДПХ в ДПФ иногда можно избежать, и пример такого подхода рассматривается при умножении длинных чисел.

Параллелизм на уровне инструкций процессора также приблизительно одинаковый, поэтому реальная эффективность практически одна и та же. Однако, есть несколько моментов, которые отличаются.

–          Код для БПХ проще. Формула обратного преобразования совпадает с формулой для прямого, за исключением множителя 1/N, в то время как при вычислении обратного БПФ приходится вводить дополнительный параметр или делать новую функцию.

–          Точность БПХ, как правило, немного выше, чем у БПФ.

–          При вычислении БПФ действительного вектора сначала вычисляется “комплексное” БПФ половинной длины, а потому производится послеобработка, которая отсутствует в БПХ.

Это даёт БПХ дополнительное упрощение кода, по сравнению с БПФ и влияет на эффективность при малых длинах векторов. Однако, чем длиннее вектор — тем это влияние слабее [3].

Модель на основе преобразования Фурье

На рисунке 1 изображена модель канала связи на основе преобразования Фурье разработанная в среде Simulink.

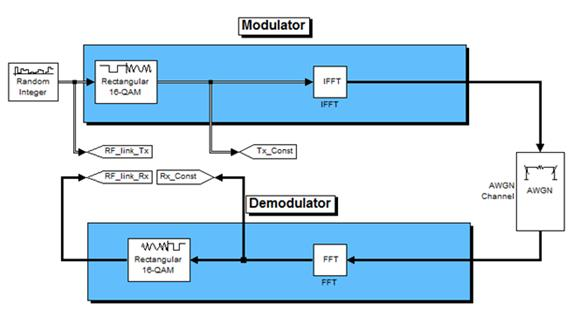
Рис. 1. Модель канала связи на основе преобразования Фурье

 

Блок Random Integer — генератор псевдослучайных чисел выступает в роли источника сообщений. От источника сообщений данные поступают в модулятор, который состоит из двух блоков. Первый Rectangular 16-QAM — квадратурный модулятор. Модулированный сигнал поступает на блок IFFT — обратного быстрого преобразования Фурье. После преобразования сигнала в модуляторе данные поступают в канал связи на блок AWGN — аддитивный белый гауссовский шум. После канала связи сигнал передаётся в модулятор, который состоит из двух блоков. Первый блок FFT — быстрого преобразования Фурье. Далее на Rectangular 16-QAM — квадратурный демодулятор.

С входа модулятора и выхода демодулятора через ярлыки RF_link_Tx и RF_link_Rx, соответственно, данные передаются в блок расчёта коэффициента ошибочных битов.

Результаты анализа модели по коэффициенту ошибочных битов при различных отношениях сигнал/шум приведены в таблице 1.

Таблица 1

Средние значения коэффициента ошибочных битов при различных отношениях сигнал/шум

 

Модель модема на основе преобразования Хартли

На рисунке 2 изображена модель модема на основе преобразования Хартли разработанная в среде Simulink.

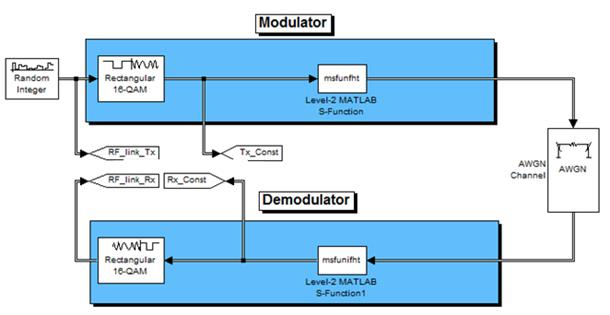
Рис. 2. Модель модема на основе преобразования Хартли

 

Модулированный сигнал поступает на блок msfunfht — быстрого преобразования Хартли, которых в схеме два одинаковых в передатчике и приемнике.

Результаты анализа модели по коэффициенту ошибочных битов при различных отношениях сигнал/шум приведены в таблице 2.

Таблица 2

Средние значения коэффициента ошибочных битов при различных отношениях сигнал/шум

 

Обобщённые графики зависимостей коэффициента ошибочных битов от отношения сигнал/шум для модемов на основе преобразования Фурье, преобразования Хартли изображены на рисунке 3.

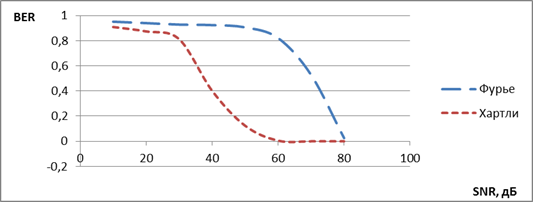
Рис. 3. Зависимости коэффициента ошибочных битов от отношения сигнал/шум

 

Выигрыш преобразования Хартли перед преобразованием Фурье по коэффициенту ошибочных битов порядка 25дБ.

 

Литература:

 

1.      Брейсуэлл Р. Преобразование Хартли. Теория и приложения: [пер. с англ.] / под ред. И. С. Рыжака. — М.: Мир 1990. — 175 с.

2.      Слюсар В. И. Метод неортогональной частотной дискретной модуляции на основе преобразования Хартли с квадратурной амплитудной модуляцией частотных несущих. / В. И. Слюсар, В. Г. Смоляр. // Системы обработки информации. -2008.- вып. № 2, С.102–104.

3.      Слюсар В. И. Метод неортогональной частотной дискретной модуляции для узкополосных каналов связи. / В. И. Слюсар, В. Г. Смоляр. // Радиоэлектроника. -2004.- вып. № 4, С.: 53–59.