Организация самостоятельной работы выпускников в рамках подготовки к ЕГЭ по математике с применением программного обеспечения GeoGebra
Авторы: Данелян Сусанна Амирбековна, Данелян Иринэ Игоревна
Рубрика: 12. Технические средства обучения
Опубликовано в
II международная научная конференция «Педагогическое мастерство» (Москва, декабрь 2012)
Статья просмотрена: 401 раз
Библиографическое описание:
Данелян, С. А. Организация самостоятельной работы выпускников в рамках подготовки к ЕГЭ по математике с применением программного обеспечения GeoGebra / С. А. Данелян, И. И. Данелян. — Текст : непосредственный // Педагогическое мастерство : материалы II Междунар. науч. конф. (г. Москва, декабрь 2012 г.). — Москва : Буки-Веди, 2012. — URL: https://moluch.ru/conf/ped/archive/65/3185/ (дата обращения: 26.04.2024).
Федеральный государственный образовательный стандарт среднего (полного) общего образования обсуждается сегодня повсеместно.
«Методологической основой Стандарта является системно-деятельностный подход, который обеспечивает формирование готовности обучающихся к саморазвитию и непрерывному образованию…» [1].
Стандарт устанавливает требования к результатам освоения обучающимися основной образовательной программы:
личностным, включающим готовность и способность обучающихся к саморазвитию, метапредметным, включающим освоенные обучающимися межпредметные понятия, способность их использования на практике, самостоятельность в планировании и осуществлении учебной деятельности и организации сотрудничества с педагогами и сверстниками, владение навыками учебно-исследовательской, проектной деятельности.
Автор статьи организует занятия элективных курсов по решению заданий повышенного и высокого уровня (группы С) в рамках подготовки к ЕГЭ, делая основной акцент на самостоятельные разработки обучающихся, координируя и направляя организацию работы как в индивидуальной так и в групповой форме, используя метапредметные связи, и, в первую очередь, возможности преподавания информатики и информационных технологий в единстве с математикой. Использование технических средств обучения (интерактивной доски, проектора) дает возможность очень эффективно использовать при этом интерактивную среду программы GeoGebra [3]. Это обучающая программа по математике, разработана для изучения и обучения в школе. С ее помощью можно анализировать функции, строить их графики, решать задачи по геометрии.
В зависимости от уровня подготовки слушателей курса проводятся в разном объеме подготовительные пропедевтические разработки и разборы заданий повышенного и высокого уровня. Соответственно распределяются между выпускниками и задания для самостоятельной подготовки.
На одном из занятий элективного курса по математике «Решение заданий с параметрами (С5) с применением программного обеспечения GeoGebra» (технология решения заданий с параметрами с использованием интерактивной среды программы GeoGebra и эффективность её использования описаны в статьях автора [2], [3]) проводится разбор следующего задания высокого уровня сложности:
Найдите, при каких значениях параметра а системы уравнений
![]()
имеют одинаковое число решений.
До проведения занятия проводится предварительное распределение заданий для самостоятельной работы в соответствии с уровнем подготовки слушателей курса:
* обучающимся, недостаточно знакомым с библиотекой графиков и уравнений, не имеющим необходимых навыков в использовании графической культуры, предлагается с помощью программного обеспечения GeoGebra подготовить к занятию пропедевтические презентации по темам:
Графики функций обратной пропорциональности y=1/x, y=1/x. Сделать вывод: как по виду графика функции y=f(x) строится график функции y=f(x);
График уравнения x+y=а. Последовательно записывая в ПО GeoGebra в строку ввода уравнения x+y=а, x+y=а, x+y=а для некоторого конкретного числа а, сделать вывод о влиянии знака модуля на вид графика уравнения. Далее, применив ползунок для значений а, определить влияние значения параметра а на изменения графика уравнения;
График линейной функции y =-х+n. Сделать вывод о роли параметра n на положение графика функции, организовав при использовании ПО GeoGebra ползунка для параметра n;
Уравнение окружности (х-а)2+(у–b)2= R2. Задать ползунки для значений параметров а, b, R, сделать вывод об их роли при построении графика заданного уравнения.
* более подготовленных обучающихся можно объединить в группы (возможен и индивидуальный подход) – первой группе поручить подготовить презентацию решения первого уравнения системы, а второй группе – второго уравнения системы. Самым сильным обучающимся можно поручить подготовить проект решения всего задания.
При использовании ПО GeoGebra после записи в строку ввода аналитического задания рассматриваемой функции или уравнения, обучающиеся предварительно определяют интервалы движения для каждого из ползунков, соответствующих параметрам рассматриваемого уравнения или функции. Двигая ползунки, определяющие динамику соответствующих параметров, учащиеся на начальном этапе изучения графической культуры самостоятельно делают выводы о влиянии каждого из параметров на вид графика заданной функции или уравнения. Обучающиеся, недостаточно знакомые с библиотекой графиков и уравнений, при этом имеют возможность с помощью графических иллюстраций, полученных при применении ПО GeoGebra, освоить и закрепить знания из раздела построения графиков элементарных функций и уравнений.
На занятии, в зависимости от уровня подготовки группы элективного курса, отводится соответственно больше или меньше времени на рассмотрение презентаций, подготовленных в рамках пропедевтики базовых знаний и умений. После чего группа переходит к разбору собственно самого задания.
Первая группа представляет первую систему:
Преобразуем первое уравнение системы при х 0, у >0:
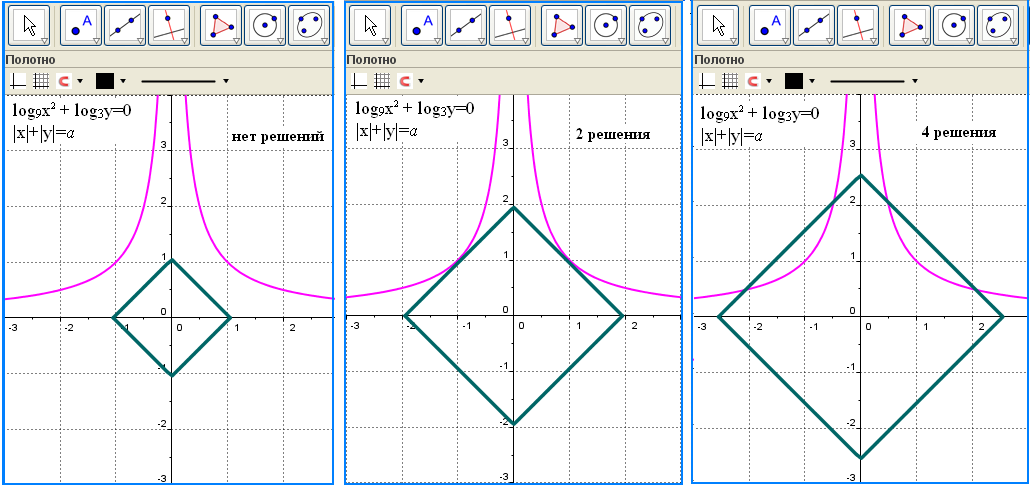
log9x2 + log3y=0 log3x + log3y=0 x y=1 y=1/x.
y=1/x – функция обратной пропорциональности, графиком которой являются две ветви гиперболы, расположенные в первой и третьей координатных четвертях. График функции y=1/x получаем симметричным отображением относительно оси абсцисс ветви гиперболы, расположенной в третьей четверти, во вторую координатную четверть.
x+y=a, при а<0 уравнение не имеет решений, при а=0 график уравнения вырождается в точку (0;0), построим график уравнения при а >0: y=-x+a : при у>0 y=-x+a – прямой угол с вершиной в точке (0;а), стороны которого направлены вниз, при у=0 получаем точки на оси х (-а;0), (а;0), при у <0 y=x-a получаем прямой угол с вершиной в точке ( 0: а) и сторонами, направленными вверх.
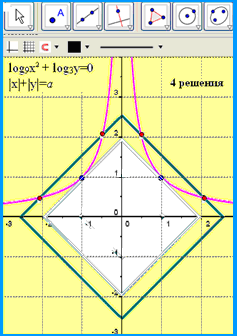
Таким образом, графиком уравнения является квадрат с центром в начале координат и вершинами, лежащими на осях координат. Параметр а задает длину 1/2 диагонали квадрата. Динамика графической интерпретации системы показывает, что с увеличением параметра квадрат расширяется и при а<2 общих точек у графиков уравнений нет, при а=2 два решения, а при а>2 система будет иметь 4 решения.
Таким образом, делается вывод: возможное количество решений первой системы представляет собой конечное множество, состоящее из трех значений {0; 2; 4}.
Разбор сопровождается красочной презентацией, демонстрирующей динамику движения, заложенного в решении заданной системы уравнений:
Вторая группа представляет решение второй системы:
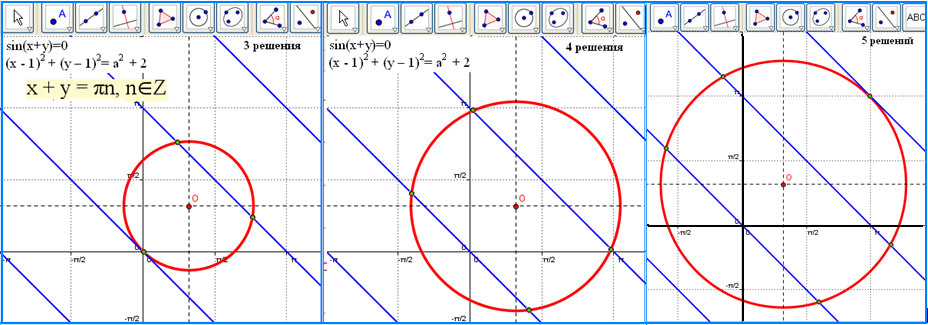
Преобразуем первое уравнение второй системы: sin(x+y)=0 x + y =n, y =-х+n, n- целое число – семейство параллельных прямых с угловым коэффициентом -1, пересекающих ось ординат в точках с координатами (0; n), n- целое число.
(х - 1)2 + (у – 1)2= а2 + 2 - уравнение окружности с центром в точке (1; 1) и радиусом, равным (а2 + 2). Наименьшее возможное значение радиуса 2, при этом у окружности с семейством параллельных прямых, задаваемых первым уравнением системы, три общие точки. Как показывает динамика рисунка, с увеличением радиуса число решений системы постепенно увеличивается и может быть любым, большим двух.
Итак, возможное количество решений второй системы представляет собой бесконечное множество, состоящее из значений {3; 4; 5….}.
Разбор системы опять-таки сопровождается красочной динамичной презентацией, демонстрирующей постепенное увеличение числа точек пересечения графиков по мере увеличения радиуса заданной вторым уравнением системы окружности:
Последним шагом занятия становится совместный анализ полученных результатов и переход к ответу на вопрос задачи: нахождение искомых значений параметра, при которых число корней заданных систем уравнений одинаково.
Сравнивая полученные множества возможного числа решений обеих систем, обучающиеся приходят к выводу, что только 4 является для систем одинаковым числом решений. Остается определить, при каких а имеют 4 решения обе системы одновременно.
Обращаемся к полученному обучающимися в ходе самостоятельной подготовки наглядному динамичному представлению: первая система имеет 4 решения при а>2, вторая система при а=0 имеет три решения, пять решений у системы при выполнении условия (а2 + 2)=(-1)2, а2 + 2=2(-1)2, а2 =22- 4 . С учетом условия а>0, а=(22- 4).
То есть, 4 решения у второй системы при 0<a<(22- 4
И, наконец, у заданных систем совпадает число решений при 2<a<(22- 4).
Промежуток 2<a<(22- 4) является решением рассматриваемого задания.
В ходе организованной самостоятельной подготовки обучающиеся осваивают владение навыками познавательной и учебно-исследовательской деятельности, способность к поиску методов решения задач; умение продуктивно общаться и взаимодействовать в процессе совместной деятельности, излагать свою точку зрения; использовать средства ИКТ.
Выпускник, принимая самостоятельное участие в подготовке занятий по разбору заданий высокого уровня из вариантов ЕГЭ, осознает ответственность за результат собственного образования, значимость своей роли в успешном решении задачи. Навыки самостоятельного приобретения знаний с использованием ИКТ-технологий являются залогом успешного продолжения выпускником учебы, формирования в дальнейшем его профессиональных компетенций.
Литература.
1. Федеральный государственный образовательный стандарт среднего (полного) общего образования Зарегистрирован Минюстом России 07.06. 2012, рег. № 24480
2. С.А. Данелян, О.Н. Колосова, Технология обучения решению задач с параметрами с использованием интерактивной среды программы GeoGebra. Материалы II международной научно-практической конференции. Пенза-Ереван-Шадринск: Научно-издательский центр «Социосфера», 2012, стр.388.
3. С.А.Данелян, О.Н. Колосова, Эффективность использования программного обеспечения GEOGEBRA при обучении задачам с параметрами. Бюллетень лаборатории математического, естественнонаучного образования и информатизации. Издательство «Научная книга», НИИ СО ГБОУ МГПУ, 2012, стр.286-291.