Система автоматизированного проектирования MathCAD в процессе формирования приемов программирования и вычислительных экспериментов в средней школе

Данная статья посвящена рассмотрению применения системы автоматизированного проектирования MathCADв процессе формирования приемов программирования и вычислительных экспериментов в средней школе. Описываются основные этапы изучения MathCADв средней школе согласно праксеологическому компоненту методики, разработанной авторами статьи. Также в статье рассматриваются примеры применения MathCADдля изучения различных тем математики и физики.

Ключевые слова:система автоматизированного проектирования, MathCAD, приемы программирования, праксеологический компонент.

Введение

Праксеологический компонент формирования приемов программирования и вычислительных экспериментов в средней школе представляется организацией системы деятельности учащихся и учителя для достижения поставленной цели. Количество часов, которые отводятся на изучение прикладного программного обеспечения, офисных пакетов, а также основ объектно-ориентированного программирования очень мало для подробного изучения их возможностей. Однако дифференцированный подход и система спецкурсов позволяют обеспечить успешность обучения для каждого учащегося за счет выбора индивидуального маршрута, который предоставляет ему возможность после достижения обязательного уровня знаний, умений и навыков осваивать дополнительное программное обеспечение, а также более детально изучать возможности сред программирования, в том числе и за счет увеличения часов самостоятельной работы. [2, с.94]

Обычно система автоматизированного проектирования (САПР) MathCAD изучается только в ВУЗах. Однако рассмотрение основ работы в ней на школьном уровне позволяет изучать некоторые темы предметов естественно-математического цикла с разных сторон, а также позволяет учащимся получить необходимые навыки для поступления в ВУЗы по техническим направлениям. [5, с.126] В рамках разработанного авторами статьи курса рассматривается возможность применения САПР MathCAD для символьных вычислений, преобразования формул, решения уравнения различных степеней, тригонометрические уравнения, а также систем линейных и нелинейных уравнений, исследования функции и построения плоских и объемных графиков (в том числе фигур, заданных параметрически). Кроме того, MathCAD используется при подготовке к ГИА и ЕГЭ.

Основные этапы изучения САПР MathCADв средней школе

Изучение САПР MathCAD состоит из нескольких этапов. Проведение этих этапов целесообразно выполнять совместно с изучением рассматриваемых тем на уроках математики и физики, что позволяет закрепить и углубить получаемые знания, а также рассмотреть области практического применения изучаемых вопросов.

Первый этап включает в себя проведения символьных вычислений. Рассматриваются базовые функции работы с формулами: упрощение выражений, разложений выражений на множители, приведение подобных слагаемых, нахождение коэффициентов полинома, разложение на элементарные дроби. Далее рассматриваются методы решения уравнений (в том числе, символьные методы), систем уравнений и нахождения корней полинома. Особое внимание уделяется наиболее сложному вопросу в данной теме — решение уравнений и неравенств, содержащих выражение под знаком модуля. Для закрепления материала учащимся предлагается самостоятельно выполнить несколько практических заданий. Кроме того, параллельно с изучением темы «Тригонометрические функции» на уроках математики, происходит изучение аналогичных вопросах на занятиях спецкурса с применение САПР MathCAD.

Второй этап направлен на формирование у учащихся навыков построения двумерных и трехмерных графиков функций. На данном этапе также рассматривается понятие полярной системы координат, обычно не изучаемая в рамках обычной школьной программы. После того, как учащиеся освоили базовые приемы построения графиков, рассматривается вопрос практического применения полученных знаний для анализа функций. Для проверки уровня усвоения материала учащиеся выполняют зачетную работу, включающую в себя задания по всем рассмотренным темам. Более сложным заданием, которое может быть предложено группе учащихся в качестве исследовательской работы, является понятие фракталов, а также их применение (в механике, для анализа финансовых рынков, для сжатия изображений и т. д.).

На третьем этапе рассматривается возможность дифференцирования функция с использованием САПР MathCAD. Учащиеся овладевают навыками вычисления первой производной, производных высших порядков, а также частных производных с использованием средств ИКТ. На данном этапе рассматриваются понятия якобиана и градиента функции. Полученные навыки учащиеся применяют при решении задач математики, физики, химии. Учащимся также предлагается выполнить исследовательский проект на тему численного дифференцирования. Данный этап включает в себя также изучение алгоритмов интегрирования, используемых в САПР MathCAD, а также рассмотрение вопросов их практического применения.

На четвертом этапе учащиеся знакомятся с элементами программирования в MathCAD. Выполнение данного этапа подразумевает знание у учащихся некоторых основ написания программного кода: понятие условных и циклических операторов, операторов присваивания, массивов. Данные теоретические знания формируются у учащихся на уроках информатики. Пятый этап направлен на закрепление и углубление имеющихся знаний.

Углубленная программа по математики включает в себя рассмотрение некоторых вопросов теории вероятностей и математической статистики. Поэтому в рамках данного спецкурса на пятом этапе учащиеся знакомятся со статистическими функциями, используемыми в САПР MathCAD. Кроме того, учащиеся знакомятся с некоторыми специфическими функциями системы MathCAD. Например, со строковыми функциями, функциями сокращения и округления, работы с комплексными числами, преобразования координат, кусочно-непрерывными функциями.

Также в рамках спецкурса при помощи САПР MathCAD можно рассмотреть темы, выходящие за пределы школьной программы. Одной из таких является тема «Матрицы». Вначале необходимо дать понятие «матрицы», а также обозначить области применения матричных вычислений. Затем рассматриваются базовые операции, выполняемые над матрицами, и специальные матричные функции в MathCAD. В рамках индивидуальной проектной работы одному из учащихся (или группе учащихся) может быть предложено изучить применения матриц для решения систем уравнений.

Еще одним вопросом, также не рассматриваемым в рамках обычной школьной программы, является понятие аппроксимации функций. Данная тема непосредственно связана с функциональным анализом и вычислительными экспериментами. Поэтому, на практических занятиях учащимся может быть предложено проинтерполировать (или экстраполировать) результаты реального физического эксперимента с применением САПР MathCAD. Группа учащихся может быть дано индивидуальное задание: обработать, произвести фильтрацию, проанализировать и интерпретировать результаты вычислительного эксперимента. Данный проект носит более обширный характер и помимо применения алгоритмов аппроксимации данных в системе MathCAD, может включать в себя написание специальных утилит, проведение дополнительных вычислений (в том числе, с применением средств ИКТ), изучение алгоритмов фильтрации, используемых в САПР MathCAD, построение графиков.

Применение САПР MathCADдля изучения некоторых тем математики и физики

Система MathCAD является отличным инструментов для выполнения различных математических расчетов, обработки данных физических экспериментов. Она имеет широкие возможности по решению уравнений и систем, дифференцированию и интегрированию, функциональному анализу, созданию и редактированию графиков функций и стереометрических фигур, аппроксимации функций. Кроме того, система позволяет обмениваться данными с другими приложениям, например, с MS Excel. Далее приведены примеры применения САПР MathCAD для изучения различных тем математики и физики, как входящих в школьную программу, так и выходящих за ее пределы.

Пример 1. Решить систему уравнений:

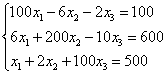
Для решения систем уравнений в MathCAD используется специальный вычислительный блок Given — Find, состоящий из четырех частей:

-        начальные приближения (т. к. для решения систем уравнений в MathCAD используются итерационные методы, то предварительно необходимо присвоить каждой переменной начальное значение, вблизи которого будет производиться поиск корня);

-        ключевое слово Given;

-        система, записанная при помощи логических операторов, в виде равенств и неравенств;

-        функция Find (x₁,x₂, …, x_n), используемая для решения системы относительно переменных x₁,x₂, …, x_n.

Для приведенной выше системы решающий блок будет иметь следующий вид:

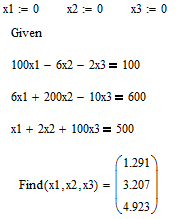
Рис. 1. Решение системы в MathCAD

Также MathCAD позволяет производить символьное решение уравнений и систем с использованием того же вычислительного блока Given — Find. Однако в данном случае, во-первых, отсутствует первая часть блока, отвечающее за задание начальных приближений переменным, во-вторых, после функции Find(x₁,x₂, …, x_n) вместо знака равенства необходимо использовать оператор «→» (EvaluateSymbolically). Кроме того, MathCAD предоставляет возможность приближенного решения уравнений и систем, например, в случае, когда невозможно найти точное решение с помощью функции Find (x₁,x₂, …, x_n). В такой ситуации можно попробовать минимизировать невязку с использованием функции Minerr(x₁,x₂, …, x_n).

Пример 2. Найти условный экстремум (максимум) функции и значение функции в точке экстремума.

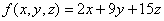
Ограничения:

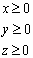
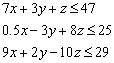
Задачи поиска экстремума функции означают нахождение ее максимума (наибольшего значения) или минимума (наименьшего значения) в некоторой области определения ее аргументов. Ограничения значений аргументов, задающих эту область, как и прочие дополнительные условия, должны быть определены в виде системы неравенств и уравнений. В таком случае говорят о задаче на условный экстремум. Для решения задач поиска максимума и минимума в MathCAD имеются встроенные функции:

-        Minimize(f,x₁,x₂, …, x_n) — вектор значений аргументов, при которых функция f достигает минимума;

-        Maximize(f,x₁,x₂, …, x_n) — вектор значений аргументов, при которых функция f достигает максимума.

Как и в случае решения систем уравнений, перед использованием данных функций всем переменным необходимо присвоить начальные значения, чтобы обозначить границы интервала, на котором происходит поиск экстремума функции. Для рассматриваемой задачи решающий блок будет иметь следующий вид:

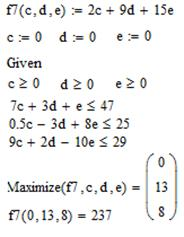
Рис. 2. Поиск условного экстремума функции с помощью MathCAD

Пример 3. Решить уравнение .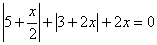

Одна из наиболее сложных тем школьного курса алгебры — решение уравнений, содержащих переменную под знаком модуля. Наиболее часто используемый способ решения таких уравнений состоит в раскрытии модуля на основании определения. Для этого необходимо оценить, при каких значениях переменной выражение, стоящее под модулем, неотрицательно, а при каких — отрицательно. Система MathCAD предлагает иной подход к решению уравнений с модулем, состоящий из следующих шагов [3, с.31]:

-        определить функцию, содержащую левую часть уравнения, при условии, что правая часть равна нулю;

-        преобразовать исходное уравнение таким образом, чтобы в левой части остался только один модуль;

-        составить две функции, отражающие левую и правую часть уравнения;

-        построить графики полученных функций в одной системе координат с помощью

-        X-YPlot, введя имена функций и аргумента в специальные заполнители и определив диапазон значений;

-        найти начальные приближения корней исходного уравнения — абсциссы точек пересечения графиков функций (масштаб области построения можно изменить);

-        найти точное значение корней уравнения при помощи функции root(f(x),x). Данная функция имеет другой формат: root(f(x),x,a,b), где f(x) — имя функции, x — имя переменной, a,b — границы интервала, внутри которого происходит поиск корня. В таком случае нет необходимости предварительно задавать начальное приближение для переменной x.

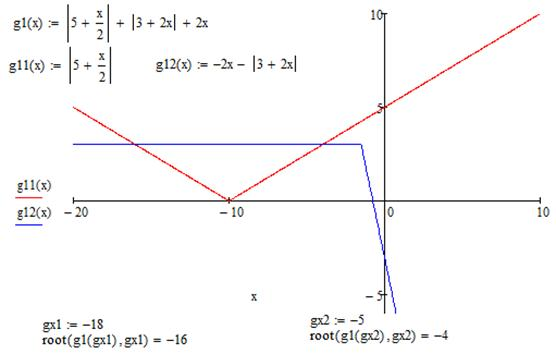
Рис. 3. Решение уравнения с модулем в MathCAD

Пример 4. Построение фигур вращения.

Построение трехмерных графиков в MathCAD осуществляется при помощи команды SurfacePlot. MathCAD интерпретирует поверхность как аппликаты точек соответствующей функции абсцисс и ординат. Поэтому вначале следует задать соответствующие значения трех матриц, определяя их как функции дискретных параметров в заданном диапазоне. Эти матрицы должны иметь одинаковое число строк и столбцов. Это можно сделать вручную или с помощью функций CreateSpace или CreateMesh, используемых для создания массива, представляющего x-, y-, z-координаты параметрической пространственной кривой или поверхности соответственно. Далее для построения поверхности необходимо ввести имена этих трех матриц в поле ввода графической области. [1, с.23]

Ниже приведен фрагмент кода в системе MathCAD для построения сферы.

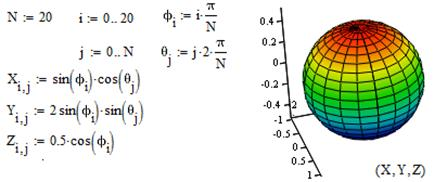
Рис. 4. Построение сферы в MathCAD

Пример 5. Аппроксимация результатов эксперимента.

Аппроксимация — научный метод, состоящий в замене одних объектов другими, в каком-то смысле близкими к исходным, но более простыми. Аппроксимация позволяет исследовать числовые характеристики и качественные свойства объекта, сводя задачу к изучению более простых или более удобных объектов. В геометрии рассматриваются аппроксимации кривых ломаными. Некоторые разделы математики, в сущности, целиком посвящены аппроксимации, например, теория приближения функций, численные методы анализа. При проведении экспериментов довольно часто возникает ситуация, когда экспериментальные данные представляются в виде массива, состоящего из пар чисел (х_iу_i). В связи с чем возникает задача аппроксимации дискретной зависимости y(x_i) непрерывной функцией f(x). Для этого в MathCAD предусмотрено несколько встроенных функций, позволяющих «соединить» точки выборки данных кривой разной степени гладкости. Существует два вида аппроксимации:

-        Интерполяция — способ нахождения промежуточных значений величины по имеющемуся дискретному набору известных значений;

-        Экстраполяция — особый тип аппроксимации, при котором функция аппроксимируется вне заданного интервала, а не между заданными значениями.

-        Экстраполяция в MathCAD осуществляется при помощи функции predict(y,m,n). Для интерполяции используются следующие функции [4, с.78]:

-        linterp(x,y,t) — линейная интерполяция;

-        interp(s,x,y,t) — кубическая или полиномиальная сплайн-интерполяция в зависимости от функции, определяющей вектор s: lspline, pspline, csplne, bspline.

Ниже представлен фрагмент программы в MathCAD, используемой для обработки данных, полученных в результате физического эксперимента на открытой воде по моделированию волнения.

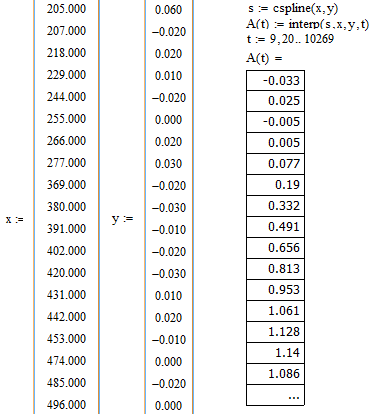
Рис. 5. Аппроксимация функций в MathCAD

Заключение

Анализируя пути реализации субъектно-деятельностной технологии приемов программирования и вычислительных экспериментов в средней школе, авторы статьи делают вывод, что данная технология есть совокупность трех взаимосвязанных между собой компонентов: когнитивного, праксеологического и психологического. Каждый по отдельности и все вместе они создают условия эффективного и наглядного, глубокого, научного, показывающего практическую значимость обучения математике, физике и информатике в средней школе.

Праксеологический компонент представляется организацией системы деятельности учащихся и учителя для достижения поставленной цели. Дифференцированный подход и система спецкурсов позволяют обеспечить успешность обучения каждого учащегося. Это обусловлено выбором индивидуального маршрута, который предоставляет возможность после достижения обязательного уровня знаний, умений и навыков осваивать дополнительное программное обеспечение, а также более детально изучать возможности среды программирования, в том числе и за счет увеличения часов самостоятельной работы. Отличительной особенностью методики, разработанной авторами статьи, является взаимосвязь различных дисциплин естественнонаучного цикла посредством проведения интегрированных уроков. Введение в школьную программу элементов программирования и вычислительных экспериментов с применением различного программного обеспечения, в том числе, САПР MathCAD, позволяет изучать отдельные темы математики, физики с различных сторон. Кроме того, на практических занятиях учащиеся могут использовать полученные знания для проведения вычислительных экспериментов, написания различных утилит и т. д. Благодаря авторской методике, учащиеся имеют возможность получить навыки работы не только с широко распространенными офисными пакетами, но и с более профессиональными, узкоспециализированными компьютерными программами.

Литература:

1.                      Алейников И. А. Практическое использование пакета MathCAD при решении задач. — М.: Российский государственный открытый технический университет путей сообщения Министерства путей сообщения Российской Федерации, 2002.

2.                      Григорьев Б. В., Чумакова В. И. Праксиология или как организовать успешную деятельность. — М.: Школьная пресса, 2002.

3.                      Охорзин В. А. Прикладная математика в системе MathCAD. — С-Пб.: Лань, 2008.

4.                      Поршнев С. В. Компьютерное моделирование физических процессов с использованием пакета MathCAD. — М.: Горячая линия — Телеком, 2002.

5.                      Сластенин В. А., Подымова Л. С. Педагогика: инновационная деятельность. — М.: ИЧП «Издательство Магистр», 1997.