Активизация учебно-познавательной деятельности студентов при изучении темы «Типичные арифметические задачи»
Автор: Стрелецкая Наталия Михайловна
Рубрика: 9. Педагогика высшей профессиональной школы
Опубликовано в
IV международная научная конференция «Педагогическое мастерство» (Москва, февраль 2014)
Дата публикации: 07.02.2014
Статья просмотрена: 115 раз
Библиографическое описание:
Стрелецкая, Н. М. Активизация учебно-познавательной деятельности студентов при изучении темы «Типичные арифметические задачи» / Н. М. Стрелецкая. — Текст : непосредственный // Педагогическое мастерство : материалы IV Междунар. науч. конф. (г. Москва, февраль 2014 г.). — Т. 0. — Москва : Буки-Веди, 2014. — С. 250-255. — URL: https://moluch.ru/conf/ped/archive/100/5070/ (дата обращения: 27.04.2024).
В статье описывается технология обучения, направленная на стимулирование учебно-познавательной активности студентов факультета «начальное обучение» педагогических вузов при изучении темы «Типичные арифметические задачи» в курсе «Математика».
Ключевые слова: арифметические задачи, трудности при решении, три уровня учебно-познавательной активности студентов, схема-ориентир решения, памятка, индивидуальная домашняя работа.
Большое внимание в курсе «Математика» для студентов факультета «начальное обучение» педагогических вузов уделяется решению арифметических задач. А именно: «на нахождение двух чисел за суммой (или разностью) и кратным отношением», «на нахождение двух чисел за суммой и разностью», «на нахождения неизвестных по двум разностям», «на предположение», «на замену», а также сюжетных арифметических задач «на движение», «на общую работу», «на дроби», «на проценты», «на смеси и сплавы». Изучение темы «Арифметические задачи» связана с разделом «Числовые множества» и рассматривается как область применения теории к таким моментам процесса решения задач, как обоснование отношений над числами и их свойствами, обоснование арифметических действий, использование техники устного и письменного выполнения действий над числами. С другой стороны, овладение студентами умениями решать арифметические задачи лежит в основании их готовности, как будущих учителей начальных классов, к обучению младших школьников решению задач. Важно заметить, что некоторые из перечисленных нами типов арифметических задач помещены в действующих учебниках по математике для 3–4 классов [1, 2] как задачи повышенной сложности — «со звездочкой». Аналогичные задачи предлагаются младшим школьникам и в олимпиадных заданиях. Они носят развивающий, пропедевтический характер, так как изучение способов их решение предусмотрено в 5–6 классах [3, с. 311]. Изучение данной темы имеет и самостоятельное значение. Студенты ознакамливаются с понятиями «арифметическая задача», «типичная арифметическая задача», классификацией арифметических задач, у них формируются как общие, так специальные подходы к решению конкретного типа задач.
Практика преподавания математики на факультете начального обучения в течении 7 лет показывает, что трудности, возникающие у студентов в связи с изучением темы часто связаны с нечетким определением связей между данными и искомыми величинами и соотнесении задачи к известному типу. Не всем одинаково легко удается применять эвристические приемы решенной задачи на задачи аналогичные по математическому содержанию путем сравнения и обобщения содержания задач.
Одной из причин такого положения мы определяем недостаточность традиционного подхода обучения, в котором решающую роль играют методы «примера» и «постепенно усложняющихся упражнений». Они не всегда содействуют формированию прочных осмысленных знаний каждым студентом, так как опираются на преимущественно пассивное восприятие и перенос новых приемов и методов решения задачи-образца в аналогичные и частично измененные условия.
В теории обучения учебно-познавательная деятельность рассматривается «как специальный процесс организации учения, непосредственной целью которого являются усвоение учащимися специально структурированных наборов знаний, умений, навыков, отношений, ценностей» [7, с. 146].
Рациональная организация процесса учения должна обеспечивать три уровня активности студентов, с преобладанием высшего уровня активности [5, 7]. Так, репродуктивно-подражательный уровень характеризуется в рамках восприятия и механического воспроизведения знаний. Частично поисково-исполнительный — проявляется в самостоятельном решении стандартных задач по инструкции или алгоритму. Творческий уровень активности обусловливается самостоятельным определением учебных целей, осмысление нешаблонных способов их решения или использование добытых знаний в нестандартных ситуациях.
Как известно, условием активизации творческой деятельности личности выступает познавательный интерес (за М.Алексеевой). Формирование познавательного интереса студентов при изучении темы «Типичные арифметические задачи» нами обеспечивалось постановкой мотивации изучения таких задач, использование мультимедийных средств, дидактических раздаточных материалов, а также использование задач, содержания которых связано с современной практической жизнью, задач исторического содержания.
Особенностью темы есть то, что ее прохождение предусмотрено на практических занятиях. В виду сложности темы «Типичные арифметические задачи» подготовка студентов к первому практическому занятию включала самостоятельную обработку лишь общих теоретических основ решения арифметических задач по заданной литературе. При такой постановке начало занятия должно проходить фронтально [6].
Результатом опроса студентов по подготовленным ими вопросам есть обобщение узловых положений теории, которое рационально представить слайдами в мультимедийной презентации (Рис.1).
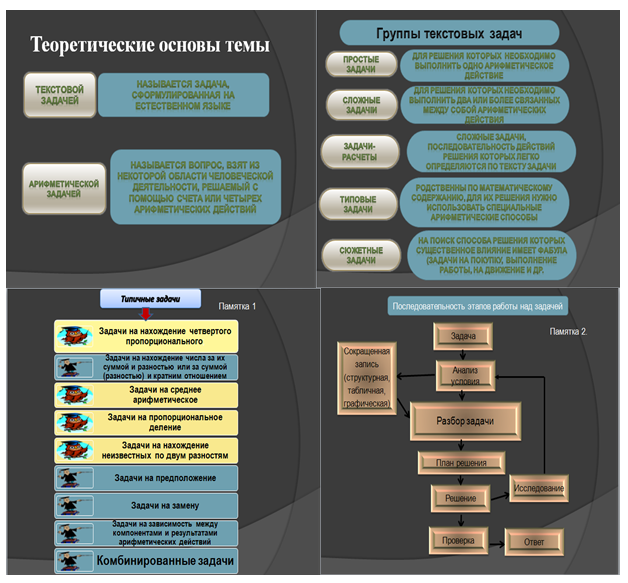
Рис. 1.
Некоторые сделанные обобщение, а также опорные схемы-ориентиры (алгоритмы) решения задач нового типа подготовлены нами и как раздаточные материалы (памятки) для каждого студента. Только после того, как одним из студентов были сформулированы (с возможными уточнениями преподавателя) определенные обобщения, разрешалось обращаться к соответственной памятке.
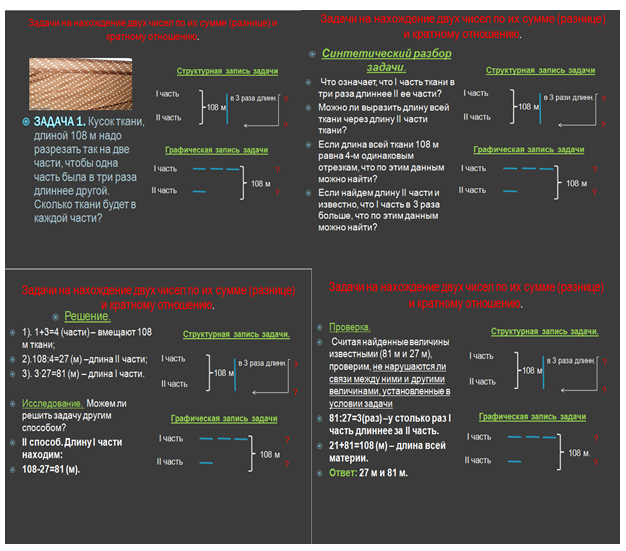
Рис. 2.
Решение первой задачи «на нахождение двух чисел за их суммой и кратным отношением» происходит фронтально и носит обучающий характер как по содержанию, так и по оформлению. Работа над задачей происходит в соответствии с Памяткой 2 и представлена слайдами мультимедийной презентации. Так, в динамичном режиме представлено оформление сокращенной записи условия задачи двумя способами (структурным и графическим). Выясняются их особенности, а также определяются существенные признаки задачи. На следующем слайде представлен разбор задачи синтаксическим способом, причем план решения дается в устной форме. Далее идут запись решения одним из способов — с комментариями к каждому действию, этап исследования задачи и этап проверки решения задачи (Рис. 2).
Для второй задачи (Рис.3) «на нахождение двух чисел за их разностью и кратным отношением» фронтальная форма работы отводится лишь на оформление сокращенной записи условия и выяснение существенных признаков задачи. Студенты самостоятельно должны сделать разбор задачи, оформить план-решение (с вопросительными предложениями плана), а также продемонстрировать остальные этапы работы над задачей в соответствии с Памяткой 2.

Рис. 3.
С целью осмысления решения задач данных типов и закрепления в памяти приемов, использованных в процессе решения, а также условий применения этих приемов в других ситуациях, целесообразна фронтальная работа студентов над созданием схемы-ориентира решения определенного типа задачи (Памятка 3). Она включает сравнительный анализ особенностей решения двух задач данного типа и выделения обобщенного алгоритма действий по их решению (Рис. 4).

Рис. 4.
Для рассмотрения следующего типа задач «на нахождение чисел за их суммой и разностью», можно предложить комбинированную задачу — состоящую из двух однотипных подзадач (со второй усложненной подзадачей).
Одной из обучающих целей такого подхода есть пропедевтика формирования умений разбивать задачи на подзадачи некоторых типов. Коллективно проводится анализ задачи и оформление сокращенных записей 1-й подзадачи, а также план-решение первой подзадачи, включающий рассуждения с эвристическими приемами. Эффективным моментом есть то, что необходимые изменения данных в условии задачи, связанные с этими приемами демонстрируются на слайде в динамическом режиме (графическая схема условия задачи) (Рис. 5).

Рис. 5.
Этап исследования и проверки подзадачи выполняется устно. Вторая подзадача решается студентами самостоятельно в соответствии с Памяткой 2. После коллективной проверки ее решения, предлагается самостоятельно сформулировать и схему-ориентир, а затем обсудить коллективно и сверить с Памяткой 4.
Работа над изучением третьего типа задач «на предположение» будет отличаться от описанной выше технологии использованием новой формы сокращенной записи — табличной, которая наиболее эффективна при наличии в условии задачи трех взаимосвязанных величин (Рис. 6, Рис. 7).
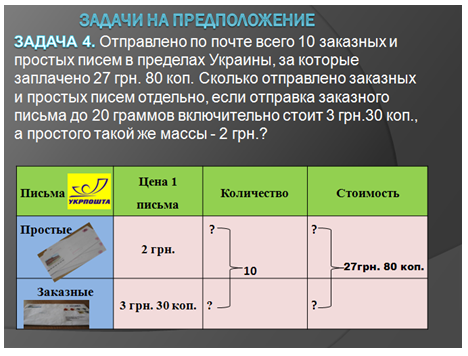
Рис. 6.

Рис. 7.
Для подготовки к следующему практическому занятию студентам дается задание самостоятельно ознакомиться с примерами решения задач «на нахождения двух чисел за двумя разностями» и «на замену» со сборника задач [4], выделить существенные признаки задач каждого типа и составить схему-ориентир их решения. Кроме этого, дается индивидуальная домашняя работа по теме «Типичные арифметические задачи», рассчитанная на месяц. Она состоит из 33 заданий и включает три уровня сложности: репродуктивный (16 задач), частично-поисковый (11 задач) и творческий (6 задач). Хотя бы часть заданий должна быть решена до следующего занятия. Первый уровень заданий состоит из задач, аналогичных решенным на занятиях. Второй уровень включает типичные задачи с усложненным условием или комбинированные. Третий — предусматривает задания на выбор:
1) составление студентами задач изученных типов с решением и оформления презентации или электронного пособия по решению типичных арифметических задач;
2) изучение дополнительной литературы и подготовка доклада (реферата) по решению типичных арифметических задач, не рассматриваемых на занятиях («на нахождение четвертого пропорционального», «на среднее арифметическое», «на пропорциональное деление», «на зависимость между компонентами и результатами арифметических действий»).
Частично опережающий характер индивидуальной домашней работы студентов обеспечивает индивидуализацию и дифференциацию обучения, прочное закрепление знаний, способствует формированию алгоритмических и эвристических приемов умственной деятельности, умению ставить цели, организации своей деятельности для их достижения. Происходит формирование и личных качеств студентов, познавательных мотивов учебной деятельности.
В начале второго практического занятия данной темы актуализируются знания студентов, усвоенные на предыдущем занятии, проверяется, корректируется и оценивается исследовательская работа студентов (на умение выделять существенные признаки задач и составлять схемы-алгоритмы их решения). Основной частью этого занятия есть решение усложненных и комбинированных задач изученных типов. До начала следующего практического занятия (на котором будут рассматриваться сюжетные задачи «на движение») студенты должны закончить и сдать индивидуальную домашнюю работу. Ее оценивание происходит в соответствии с рейтинговой системой. Задания же творческого уровня выборочно демонстрируются и обсуждаются в выбранное преподавателем на занятии время.
Применение описанной технологии, содействующей активизации учебно-познавательной деятельности студентов, существенно повысили их интерес к изучению темы «Типичные арифметические задачи». Студенты активно ведут себя на занятии, демонстрируют сознательность и прочность усвоенных знаний, с удовольствием выполняют домашние задания, консультируются по поднятым на занятии вопросам. Все это способствует профессиональному становлению будущего специалиста, раскрытию его индивидуальности и творческого потенциала.
Литература:
1. Богданович М. В. Математика: Підруч. для 3 кл. — 3-тє вид. / М. В. Богданович.– К.: Освіта — 2006. — 160 с.
2. Богданович М. В. Математика: Підруч. для 4 кл.∕ М. В. Богданович. — К.: Освіта. — 2007. — 159 с.
3. Богданович М. В. Методика викладання математики в початкових класах: Навч.пос. — з-тє вид., переробл. і доп. ∕ М. В. Богданович, М. В. Козак, Я. А. Король. — Тернопіль: Навчальна книга — Богдан, 2010. — 336 с.
4. Боровик В. Н. Збірник задач з математики. Частина 2. Навчальний посібник./ В. Н. Боровик, І.В. Зайченко, А. В. Рудник. — Чернігів: Б.в., 2005. — 272 с.
5. Вергасов В. М. Активизация познавательной деятельности студентов в высшей школе. / В. М. Вергасов. — К.: Вища школа, 1985. — 176 с.
6. Вірченко Н. О. Нариси з методики викладання вищої математики / Н. О. Вірченко. — К.:ТОВ «Задруга», 2006. — 396 с.
7. Чернецька Т.І. теорія і практика моделювання: [навч. посібник]/Т.І. Чернецька. — К.: ТОВ «Праймдрук», 2011. — 352 с.
Ключевые слова
арифметические задачи, трудности при решении, три уровня учебно-познавательной активности студентов, схема-ориентир решения, памятка, индивидуальная домашняя работа., индивидуальная домашняя работаПохожие статьи
Методы и приемы решения практических задач
Решение практических задач — это целая система последовательных действий.
Применим формулу, чтобы записать для одного из сотрудников его часть по отношению к остальным: , где. — соотношение частей.
Обучение решению арифметических задач | Статья в журнале...
При решении составных задач учащихся следует научить общим приемам работы над задачей; умению анализировать содержание задачи, выделяя известные данные, искомое (т. е. устанавливая, что нужно узнать в задаче)
Методы и приемы решения практических задач.
Роль задач в обучении математике | Статья в журнале...
Поэтому при обучении решению задач необходимо специально анализировать с учащимися связь и отношения элементов задачи.
При решении задач часто приходится обращаться к памяти. Индивидуальная память способного к математике ученика сохраняет не всю...
Ситуационная задача как один из современных методических...
Данные проблемы на уроках позволяет решать именно такая форма работы как ситуационная задача. Цель включения ситуационных задач в образовательный процесс — научить учащихся: ‒ отбирать информацию; ‒ сортировать ее для решения заданной задачи
Способы организации индивидуальной работы на уроках...
индивидуальная работа, ученик, учащийся, учитель, урок математики, положительное отношение, работа, учебный материал, задача учителя, диагностическая карта.
Разноуровневое и дифференцированное обучение как фактор...
3 уровень — продвинутый (С). Существенно углубляет материал, дает его логическое обоснование, открывает перспективы творческого применения.
Если учащиеся интересуются предметом, знают больше остальных, могут находить свой способ решения задач; способны...
Необходимость использования прикладных задач в обучении...
- способы и методы решения задач должны быть приближены к практическим приемам и методам
Основными принципами работы над задачей являются: 1. методическая обработка задачи согласно целям обучения и требованиям к системе задач.
Активизация познавательных процессов в курсе математики...
Координатная плоскость, минута, информационная компетентность, урок, координата, работа, решение задач, осмысление информации
1.2. Занятия кружка «Архимед» для рассмотрения общих методов решения задач, часто таких, которые на обычных уроках не рассматриваются.
Обобщенный способ рассуждения при решении математической...
задача, кратное отношение, род, результат решения, часть пути, значение величины первого рода, значение кратного отношения, значение величины второго рода, учебная задача, Артем.
Похожие статьи
Методы и приемы решения практических задач
Решение практических задач — это целая система последовательных действий.
Применим формулу, чтобы записать для одного из сотрудников его часть по отношению к остальным: , где. — соотношение частей.
Обучение решению арифметических задач | Статья в журнале...
При решении составных задач учащихся следует научить общим приемам работы над задачей; умению анализировать содержание задачи, выделяя известные данные, искомое (т. е. устанавливая, что нужно узнать в задаче)
Методы и приемы решения практических задач.
Роль задач в обучении математике | Статья в журнале...
Поэтому при обучении решению задач необходимо специально анализировать с учащимися связь и отношения элементов задачи.
При решении задач часто приходится обращаться к памяти. Индивидуальная память способного к математике ученика сохраняет не всю...
Ситуационная задача как один из современных методических...
Данные проблемы на уроках позволяет решать именно такая форма работы как ситуационная задача. Цель включения ситуационных задач в образовательный процесс — научить учащихся: ‒ отбирать информацию; ‒ сортировать ее для решения заданной задачи
Способы организации индивидуальной работы на уроках...
индивидуальная работа, ученик, учащийся, учитель, урок математики, положительное отношение, работа, учебный материал, задача учителя, диагностическая карта.
Разноуровневое и дифференцированное обучение как фактор...
3 уровень — продвинутый (С). Существенно углубляет материал, дает его логическое обоснование, открывает перспективы творческого применения.
Если учащиеся интересуются предметом, знают больше остальных, могут находить свой способ решения задач; способны...
Необходимость использования прикладных задач в обучении...
- способы и методы решения задач должны быть приближены к практическим приемам и методам
Основными принципами работы над задачей являются: 1. методическая обработка задачи согласно целям обучения и требованиям к системе задач.
Активизация познавательных процессов в курсе математики...
Координатная плоскость, минута, информационная компетентность, урок, координата, работа, решение задач, осмысление информации
1.2. Занятия кружка «Архимед» для рассмотрения общих методов решения задач, часто таких, которые на обычных уроках не рассматриваются.
Обобщенный способ рассуждения при решении математической...
задача, кратное отношение, род, результат решения, часть пути, значение величины первого рода, значение кратного отношения, значение величины второго рода, учебная задача, Артем.











