В работе исследовано предельное состояние анизотропного клина и штампа при действии равномерного давления. Изучено влияние смещения поверхности текучести при идеальнопластической анизотропии на величину предельного давления при вдавливании жестких штампов и клинов в идеальнопластическое полупространство. Проведен сравнительный анализ влияния трансляционной анизотропии при вдавливании жестких штампов и клинов в идеальнопластическое полупространство на величину предельных усилий вдавливания.
Ключевые слова: предельное состояние, трансляционная анизотропия, штамп, клин, усилия вдавливания, предельное давление.
Обычно анизотропия идеальнопластических тел описывается путем исследования условия текучести в форме Мизеса-Хилла. В работе исследуется представление о трансляционной идеальнопластической анизотропии, предложенной Д. Д. Ивлевым с сотрудниками [2].
Предельное условие в случае трансляционной идеальнопластической анизотропии для случая плоской деформации имеет вид
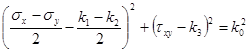 , (1)
, (1)
где 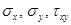 — компоненты напряжения,
— компоненты напряжения, 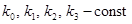 .
.
При 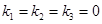 имеет место анизотропия по Хиллу.
имеет место анизотропия по Хиллу.
В дальнейшем перейдем к безразмерным величинам и отнесем все величины, имеющие размерность напряжений к величине 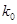 . Сохраним обозначения для компонент напряжений и постоянных
. Сохраним обозначения для компонент напряжений и постоянных 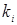
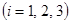 . Условие (1) примет вид
. Условие (1) примет вид
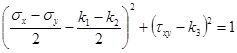 . (2)
. (2)
Преобразуем соотношение (2) и получим
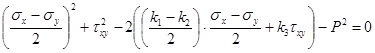 , (3)
, (3)
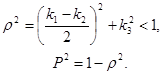 (4)
(4)
В дальнейшем положим
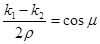 ,
, 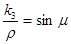 ,
, 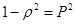 . (5)
. (5)
Воспользуемся заменой
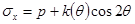 ,
,
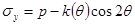 , (6)
, (6)
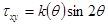 .
.
Согласно (4) − (6) условие пластичности (3) примет вид
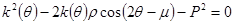 . (7)
. (7)
Так как 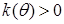 , то в дальнейшем следует ограничиться решением уравнения (7)
, то в дальнейшем следует ограничиться решением уравнения (7)
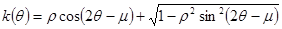 , (8)
, (8)
где 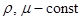 .
.
Из (8) найдем
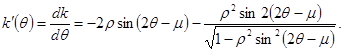 (9)
(9)
Уравнения равновесия имеют вид
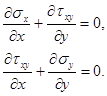 (10)
(10)
Согласно [3] из (6), (8), (9) характеристики системы уравнений (10) примут вид
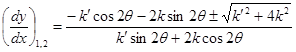 , (11)
, (11)
где 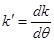 .
.
Характеристики (11) взаимно ортогональны. Соотношения вдоль характеристик, обобщающие интегралы Генки, имеют вид
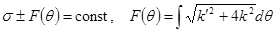 . (12)
. (12)
Рассмотрим задачу о нахождении предельной нагрузки клина при действии равномерного давления 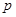 , приложенного к правой грани. Остановимся на случае тупого клина с углом раствора
, приложенного к правой грани. Остановимся на случае тупого клина с углом раствора 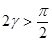 (рис. 1). Материал клина предполагается анизотропным, однородным, жестко-пластическим.
(рис. 1). Материал клина предполагается анизотропным, однородным, жестко-пластическим.
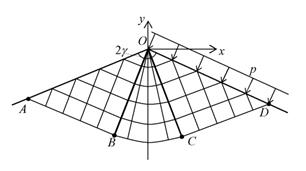
Рис. 1. Вдавливание тупого клина в анизотропную идеальнопластическую среду
Предельное давление равно [1]
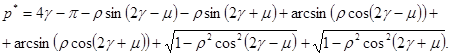 (13)
(13)
На рис. 2. представлена зависимость величины предельного давления от угла раствора 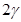 анизотропного и изотропного клина при
анизотропного и изотропного клина при 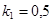 ,
, 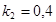 ,
, 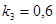 .
.
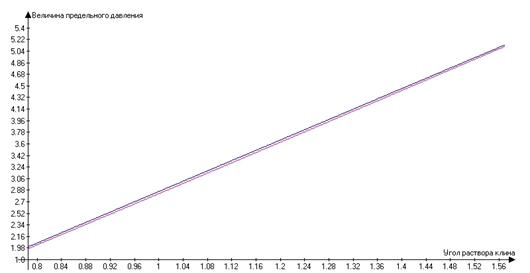
Рис. 2. Зависимость величины предельного давления от угла раствора
Таким образом, с увелеличением угла раствора величина предельного давления клина увеличивается как в изотропном, так и в анизотропном случае.
Найдем величину предельного давления тупого клина при различных 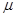 .
.
При 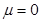 предельное давление тупого клина имеет вид
предельное давление тупого клина имеет вид
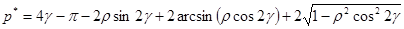 .
.
При 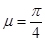 предельное давление тупого клина равно
предельное давление тупого клина равно
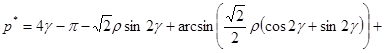
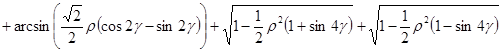 .
.
При 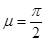 предельное давление тупого клина примет вид
предельное давление тупого клина примет вид
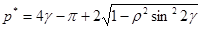 .
.
Рассмотрим задачу о вдавливании плоского гладкого штампа в анизотропное идеальнопластическое полупространство (рис. 3).
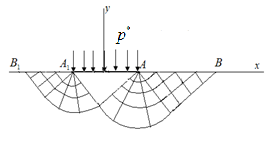
Рис. 3. Вдавливание штампа в анизотропную идеальнопластическую среду
Давление под штампом определяется по формуле [4]
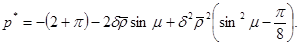 (14)
(14)
Найдем величину предельного давления под штампом при различных 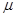 .
.
При 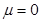 (рис. 4) предельное давление под штампом имеет вид
(рис. 4) предельное давление под штампом имеет вид
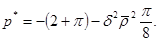
При 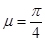 (рис. 5) предельное давление под штампом имеет вид
(рис. 5) предельное давление под штампом имеет вид
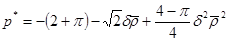 .
.
При 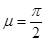 (рис. 6) предельное давление под штампом имеет вид
(рис. 6) предельное давление под штампом имеет вид
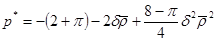 .
.
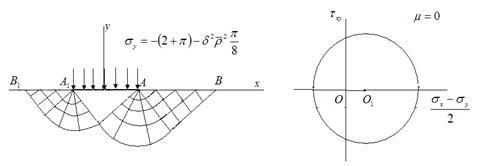
Рис. 4. Предельное давление под штампом при 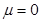
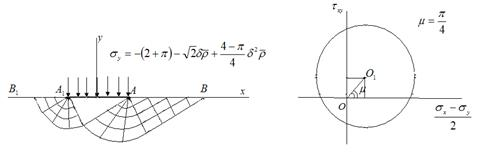
Рис. 5. Предельное давление под штампом при 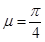 .
.
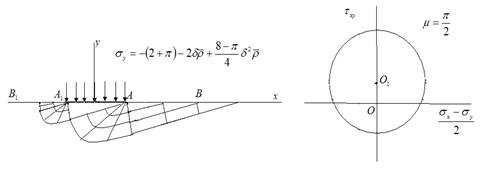
Рис. 6. Предельное давление под штампом при 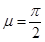 .
.
Таким образом, получили, что с увеличением величины 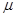 предельное давление под штампом уменьшается.
предельное давление под штампом уменьшается.
Литература:
1. Деревянных, Е. А. О предельной нагрузке клина при действии равномерного давления в случае трансляционной анизотропии / Е. А. Деревянных // Вестник Чувашского государственного педагогического университета им. И. Я. Яковлева. Серия: Механика предельного состояния. — 2012. − № 2 (12). — С. 66−70.
2. Ивлев, Д. Д. О соотношениях теории трансляционной идеальнопластической анизотропии / Д. Д. Ивлев, Л. А. Максимова, Б. Г. Миронов // Вестник Чувашского государственного педагогического университета им. И. Я. Яковлева. Серия: Механика предельного состояния. — 2010. — Т. 3. — № 2 (8). — С. 580−583.
3. Ивлев, Д. Д. Предельное состояние деформируемых тел и горных пород / Д. Д. Ивлев и др. — М.: ФИЗМАТЛИТ, 2008. — 832 с.
4. Митрофанова, Т. В. О вдавливании жесткого гладкого штампа в анизотропное идеальнопластическое полупространство / Т. В. Митрофанова // Вестник Чувашского государственного педагогического университета. Серия: Механика предельного состояния. –2011. — № 1 (9). — С. 168–176.







