Введение. Высокоэластичные материалы, способные испытывать большие деформации без разрушения, широко используются не только в различных изделиях, применимых в промышленности, но и в различных сооружениях промышленных зон и городских инфраструктур [10, 15–17]. Расчет таких изделий на прочность проводится в рамках геометрически и физически нелинейной теории упругости, в основе математической составляющей которой лежат краевые задачи для систем нелинейных дифференциальных уравнений в частных производных [3–6, 22]. Нелинейные уравнения, как правило, имеют неединственное решение [1, 22]. В задачах о сжатии тонкостенных пластин и оболочек при достижении нагрузкой некоторого критического значения происходит потеря устойчивости равновесного состояния [7, 11, 12, 14, 23, 25, 27]. Для мембран и оболочек, растягиваемых нормальным давлением, зависимость «нагрузка-деформация» может иметь точку максимума, которая так же, как и в задачах о сжатии пластин и оболочек, считается критической [5, 18, 19]. То есть одной и той же поверхностной нагрузке могут соответствовать два решения. Это следует не только из теоретических результатов, полученных при анализе статических уравнений, но и наблюдается в натурном эксперименте [6, 24, 29]. В работе ставится задача о колебаниях бесконечно длинной безмоментной цилиндрической оболочки, нагруженной нормальным внутренним давлением, и строится ее аналитическое решение. Задача о малых колебаниях моментной цилиндрической оболочки решалась в [2, 20, 21].
Разрешающие уравнения. Нелинейная связь между напряжениями и деформациями в нелинейной теории упругости определяется с помощью упругого потенциала ![]() , являющегося для изотропного материала функцией кратностей удлинений
, являющегося для изотропного материала функцией кратностей удлинений ![]() ,
, ![]() и
и ![]() . К числу потенциалов для несжимаемых материалов относятся потенциалы Муни — Ривлина, Бартенева — Хазановича, Огдена [26, 28]. Некоторые из них и их «модификации» достаточно часто используются при решении конкретных задач [3, 5, 13, 24]. Ниже будет использоваться двух параметрический степенной потенциал [6]
. К числу потенциалов для несжимаемых материалов относятся потенциалы Муни — Ривлина, Бартенева — Хазановича, Огдена [26, 28]. Некоторые из них и их «модификации» достаточно часто используются при решении конкретных задач [3, 5, 13, 24]. Ниже будет использоваться двух параметрический степенной потенциал [6]
![]() ,(1)
,(1)
где ![]() — линейный модуль сдвига,
— линейный модуль сдвига, ![]() — параметр. Из этого потенциала следуют потенциалы Бартенева-Хазановича (
— параметр. Из этого потенциала следуют потенциалы Бартенева-Хазановича (![]() ) и неогуковский (
) и неогуковский (![]() ). Для несжимаемого материала должно выполняться условие несжимаемости:
). Для несжимаемого материала должно выполняться условие несжимаемости: ![]()
Система разрешающих уравнений, описывающая колебания бесконечно длинной в направлении оси ![]() арки-полоски (рис. 1), нагруженной нормальным давлением, имеет вид [9]
арки-полоски (рис. 1), нагруженной нормальным давлением, имеет вид [9]
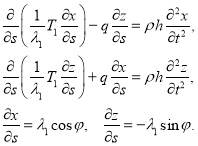 (2)
(2)
В этих уравнениях ![]() — длина дуги срединной поверхности недеформированной арки-полоскии,
— длина дуги срединной поверхности недеформированной арки-полоскии, ![]() — угол между осью
— угол между осью ![]() и нормалью к срединной поверхности в деформированной конфигурации,
и нормалью к срединной поверхности в деформированной конфигурации, ![]() — усилие, действующее в срединной поверхности,
— усилие, действующее в срединной поверхности, ![]() — кратность удлинения дуги срединной поверхности,
— кратность удлинения дуги срединной поверхности, ![]() и
и ![]() — координаты точек срединной поверхности,
— координаты точек срединной поверхности, ![]() — внутреннее давление,
— внутреннее давление, ![]() — толщина недеформированной оболочки, а
— толщина недеформированной оболочки, а ![]() — плотность ее материала. Кратность удлинения в направлении оси
— плотность ее материала. Кратность удлинения в направлении оси ![]() считается постоянной и равной единице (
считается постоянной и равной единице (![]() ), тем самым рассматривается одноосная деформация.
), тем самым рассматривается одноосная деформация.
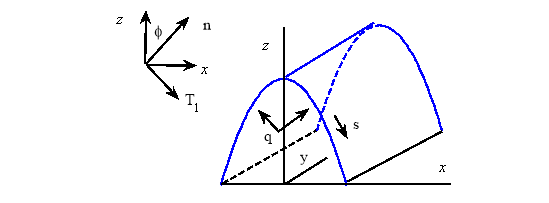
Рис. 1.
Связь между усилием и кратностью удлинения задается с помощью упругого потенциала для несжимаемого материала [5]:
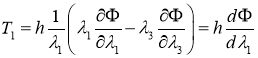 ,(3)
,(3)
в котором ![]() , а
, а ![]() . То есть упругий потенциал считается функцией двух аргументов:
. То есть упругий потенциал считается функцией двух аргументов:![]() .
.
Если края арки-полоски соединены так, что ![]() ,
, ![]() , так система уравнений (2) будет описывать динамику растяжения бесконечно длинной в направлении оси
, так система уравнений (2) будет описывать динамику растяжения бесконечно длинной в направлении оси ![]() круговой цилиндрической оболочки радиуса
круговой цилиндрической оболочки радиуса ![]() .
.
При нормальном давлении в силу симметрии задачи форма оболочки должна оставаться цилиндрической оболочкой. То есть системе уравнений (2) должно удовлетворять решение, на котором выполняются равенства ![]() ,
, ![]() ,
, ![]() (
(![]() ,
,![]() — относительное изменение радиуса оболочки). С учетом этого из (2) следует уравнение для кратности удлинения
— относительное изменение радиуса оболочки). С учетом этого из (2) следует уравнение для кратности удлинения ![]()
![]() ,(4)
,(4)
В статическом случае связь между давлением и относительным изменением радиуса оболочки определяется из зависимости ![]() . Эта зависимость может иметь точку максимума. Так, например, для упругого потенциала (1) на рис. 2 отражена зависимость безразмерного давления
. Эта зависимость может иметь точку максимума. Так, например, для упругого потенциала (1) на рис. 2 отражена зависимость безразмерного давления
![]()
от относительного увеличения радиуса оболочки для значений ![]() ,
, ![]() и
и ![]() в упругом потенциале (1). При
в упругом потенциале (1). При ![]() эта зависимость имеет асимптоту, а при
эта зависимость имеет асимптоту, а при ![]() — точку максимума (точка максимума достигается при значениях
— точку максимума (точка максимума достигается при значениях ![]() ).
).
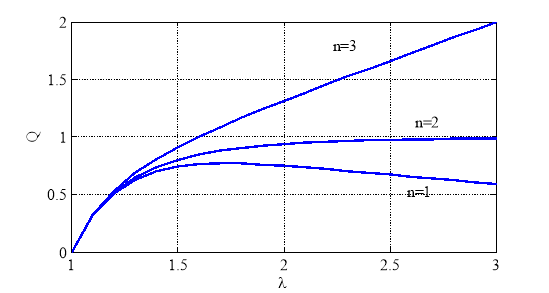
Рис. 2.
Малые колебания. Пусть цилиндрическая оболочка находится в положении равновесия, в котором
![]() .(5)
.(5)
Линеаризация уравнения (4) в окрестности этого положения равновесия приводит к линейному уравнению
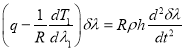 ,(6)
,(6)
в котором ![]() — малое возмущение положения равновесия.
— малое возмущение положения равновесия.
Поскольку на статическом решении выполняется равенство (5), то
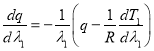 .
.
С учетом этого уравнение (6) приводится к виду
![]() .
.
На возрастающем участке зависимости ![]() (рис. 2) возникают колебания с частотой
(рис. 2) возникают колебания с частотой 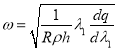 , а на убывающем участке ускорение положительно и, соответственно, будет происходить процесс постоянного расширения оболочки. То есть колебания возникают только на возрастающем участке зависимости
, а на убывающем участке ускорение положительно и, соответственно, будет происходить процесс постоянного расширения оболочки. То есть колебания возникают только на возрастающем участке зависимости ![]() .
.
Нелинейные колебания. Уравнение (4) с учетом выражения (3) для усилия ![]() приводится к виду
приводится к виду
После умножения этого уравнения на ![]() и последующего интегрирования по
и последующего интегрирования по ![]() с учетом начальных условий при
с учетом начальных условий при ![]()
![]() ,
, ![]() .(7)
.(7)
будет получено уравнение
![]() .(8)
.(8)
На решениях задачи левая часть этого уравнения не должна принимать отрицательные значения. При ![]() она обращается в ноль. Если возникают колебания, то она должна иметь хотя бы один корень
она обращается в ноль. Если возникают колебания, то она должна иметь хотя бы один корень ![]() такой, что
такой, что ![]() . Тогда на решениях уравнения (8)
. Тогда на решениях уравнения (8) ![]() будет изменяться в интервале
будет изменяться в интервале ![]() . Если при достаточно больших значениях
. Если при достаточно больших значениях ![]() упругий потенциал (1) как функция кратности удлинения
упругий потенциал (1) как функция кратности удлинения ![]() растет медленнее, чем
растет медленнее, чем ![]() , то в этом случае правая часть уравнения при достаточно больших значениях
, то в этом случае правая часть уравнения при достаточно больших значениях ![]() будет положительной и, соответственно,
будет положительной и, соответственно, ![]() будет все время расти с ростом
будет все время расти с ростом ![]() .
.
Интегрирование уравнения (8) приводит к неявной зависимости ![]()
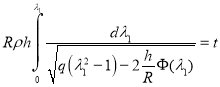 .
.
Если левая часть уравнения (8) кроме корня ![]() имеет корень
имеет корень ![]() наиболее близкий к корню
наиболее близкий к корню ![]() первой кратности, то интеграл будет сходиться, и период колебаний
первой кратности, то интеграл будет сходиться, и период колебаний ![]() будет вычисляться как
будет вычисляться как
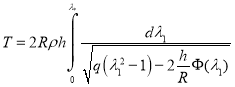
Для потенциала (1) уравнение (8) приводится к виду
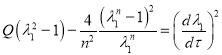 .(9)
.(9)
где 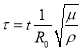 .
.
Для случая неогуковского потенциала (в (1) ![]() )
)
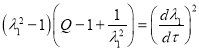 .
.
Решением этого уравнения при ![]() является функция
является функция
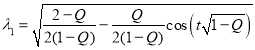 ,
,
которая является периодической с периодом колебаний
![]() .
.
При ![]() правая часть уравнения (9) обращается в ноль только в точке
правая часть уравнения (9) обращается в ноль только в точке ![]() и, соответственно, при любом малом возмущении скорости в начальный момент времени начнется процесс непрерывного увеличения радиуса деформированной оболочки.
и, соответственно, при любом малом возмущении скорости в начальный момент времени начнется процесс непрерывного увеличения радиуса деформированной оболочки.
Для ![]() уравнение (9) принимает вид
уравнение (9) принимает вид
![]() .
.
Корни правой части этого уравнения
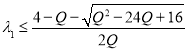 . Второй корень будет положительным при условии, что
. Второй корень будет положительным при условии, что 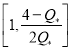 .
.
Зависимость амплитуды колебаний от параметра ![]() при начальных условиях (7) для упругого потенциала (1) с
при начальных условиях (7) для упругого потенциала (1) с ![]() ,
, ![]() и
и ![]() отражена на рис. 3. Пунктирными линиями для
отражена на рис. 3. Пунктирными линиями для ![]() и
и ![]() отмечены границы значений
отмечены границы значений ![]() , за которыми колебания прекращаются.
, за которыми колебания прекращаются.
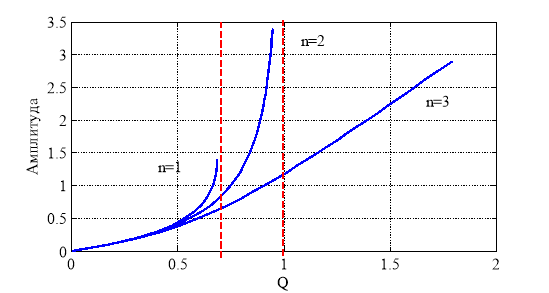
Рис. 3.
Проведенный анализ решений математической задачи о нелинейных колебаниях эластомерной оболочки не только демонстрирует возможную потерю устойчивости в условиях растяжения, но и объясняет причину потери устойчивости, связанную, прежде всего, с физической нелинейностью.
Литература:
- Екимов, А. В. Анализ множества достижимости нелинейных управляемых систем // Естественные и математические науки в современном мире. — 2014. — № 15. — С. 8–13.
- Кабриц, С. А., Еременко В. Р., Маюшан В. В., Ложкин Е. Н. Расчет напряженно-деформированного состояния цилиндрической оболочки по заданным перемещениям // Молодой ученый. — 2016. — № 12 (116). — С. 23–28.
- Кабриц, С. А., Черных К. Ф. Нелинейная теория изотропно упругих тонких оболочек с учетом поперечного сдвига // Известия Российской академии наук. Механика твердого тела. — 1996. — № 1. — С. 124.
- Кабриц, С. А., Шамина В. А. Изгиб оболочки вращения поперечной силой и моментом // Вестник Санкт-Петербургского университета. Серия 1. Математика. Механика. Астрономия. — 2014. — Т. 1. — № 2. — С. 261–270.
- Колпак, Е. П., Мальцева Л. С. Большие деформации резиновых мембран // Молодой ученый. — 2014. — № 16 (75). — С. 78–84.
- Колпак, Е. П., Мальцева Л. С. Круглая плоская мембрана при больших деформациях // Приволжский научный вестник. — 2014. — № 11–1 (39). — С. 5–10.
- Колпак, Е. П., Мальцева Л. С. Об устойчивости сжатых пластин // Молодой ученый. — 2015. — № 14. — С. 1–8.
- Колпак, Е. П. Вычисления в Matlab / учебное пособие. Казань, 2016.
- Мальцева, Л. С., Колпак Е. П., Иванов С. Е. Нелинейные колебания резиновой мембраны // Молодой ученый. — 2016. — № 8 (112). — С. 11–21.
- Пневматические строительные конструкции / В. В. Ермолов, У. У. Бэрд, Э. Бубнер и др. М.: Стройиздат, 1983. — 489 с.
- Пронина, Ю. Г Оценка устойчивости упругой трубы под давлением коррозионных сред // Вестник Санкт-Петербургского университета. Серия 10. Прикладная математика. Информатика. Процессы управления. — 2006. — № 3. — С. 55–63.
- Пронина, Ю. Г. О сосредоточенных воздействиях у границы упругой пластины // Труды ЦНИИ им. акад. А. Н. Крылова. — 2010. — № 53. — С. 117–122.
- Седова, О. С., Пронина Ю. Г О выборе эквивалентного напряжения в задачах о механохимической коррозии сферических элементов // Вестник Санкт-Петербургского университета. Серия 10. Прикладная математика. Информатика. Процессы управления. — 2016. — № 2. — С. 33–44.
- Старков, В. Н., Степенко Н. А. Исследование динамики маятниковых систем с переменными параметрами // Естественные и математические науки в современном мире. — 2014. ‑№ 15. — С. 20–36
- Старкова, Н. В. Особенности демографического развития районов Ленинградской области // Вестник Санкт-Петербургского университета. Серия 7. Геология. География. — 2007. — № 4. — С. 87–97.
- Старкова, Н. В. Особенности социально-экономического развития приграничных муниципальных районов ленинградской области // В сборнике: Стратегия развития приграничных территорий: традиции и инновации Материалы международной научно-практической конференции. 2014. — С. 350–359.
- Старкова, Н. В., Ложкинс А. Кластеризация стран Европы по демографическим признакам // Молодой ученый. — 2016. — № 9 (113). — С. 418–426.
- Bochkareva, N. L., Kolpak E. P. On stability of arch damper // Vestnik Sankt-Peterburgskogo Universiteta. Ser 1. Matematika Mekhanika Astronomiya. — 1993. — № 4. — PP. 49–53.
- Kabrits, S. A., Kolpak E. P., Chernykh K. F. Square membrane under large deformations // Mechanics of solids. — 1986. — № 21. — PP. 182–186.
- Kabrits, S. A., Shamina V. A. cylindrical shell under the action of the ring load // В сборнике: 2015 International Conference on Mechanics — Seventh Polyakhov's Reading 2015. С. 7106735.
- Kabrits, S. A., Slepneva L. V. Small nonsymmetric oscillations of viscoelastic damper under massive body action Вестник Санкт-Петербургского университета. Серия 1. Математика. Механика. Астрономия. — 1998. — Т. 2. — № 1998. — С. 78.
- Kabrits, S., Terent'ev V. Numerical solution of one-dimensional nonlinear statics problems for elastic rods and shells in the presence of rigid constraits // International Applied Mechanics. — 1984. — Т. 20. — № 7. — С. 672–675.
- Kanner, L. M., Horgan C. O. Elastic instabilities for strain-stiffening rubber-like spherical and cylindrical thin shells under inflation // International Journal of Non-Linear Mechanics. — 2007. — V. 42. — P. 204–215.
- Kolpak, E. P., Maltseva L. S. Rubberlike membranes at inner pressure // Contemporary Engineering Sciences. — 2015. — Т. 8. — № 33–36. — С. 1731–1742.
- Kolpak, E. P., Maltseva L. S., Ivanov S. E. On the stability of compressed plate // Contemporary Engineering Sciences. — 2015. — Т. 8. — № 20. — С. 933–942.
- Ogden, R. W., Saccomandi G., Sgura I. Fitting hyperelastic models to experimental data, Comput. Mech. — 2004. — V. 34. — P. 484–502.
- Polyakhova, E. N., Starkov V. N., Stepenko N. A. Solar sailing out of ecliptic plane // В сборнике: 2015 International Conference «Stability and Control Processes» in Memory of V. I. Zubov (SCP)2015. С. 65–68.
- Rivlin, R. S., Large elastic deformations of isotropic materials. VI. Further results in the theory of torsion, shear and flexure, Philos. Trans. R. Soc. London, Ser. A 42. — 1949. — P. 173–195.
- Seong-Ryoel, H., Kye-Kwang, C. Experimental study for mechanical properties of Thermoplastic Vulcanizates // Indian Journal of Science and Technology. — 2015. — V. 8. — P. 139–143.







