Введение
Моделирование поведения различных сред под воздействием внешних сил имеет большое значение для многих прикладных областей: материаловедение, машиностроение, геологические отрасли науки. Пористые металлы – достаточно новые, перспективные материалы. Для них характерны низкая плотность и способность поглощать большое количество энергии в процессе деформации при относительно низком уровне напряжения. Исследованию свойств пористых металлов и их поведения при деформации посвящены работы многих зарубежных и отечественных исследователей.
Модель
При построении модели используется реологический метод. На рис. 1 приведена реологическая схема пористой среды [1].
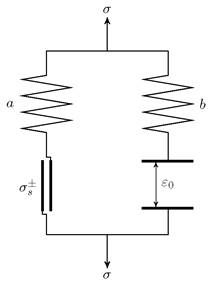
Рис. 1. Реологическая схема
В этой схеме поведение пористого металла до момента схлопывания пор имитирует пружина с модулем упругой податливости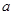 
, а повышение жесткости после схлопывания пор – пружина с модулем 
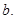Жесткий контакт описывает пороговое повышение жесткости среды при уплотнении. Также эта схема учитывает пластические свойства пористого металла.
Диаграмма связи между напряжением и деформацией пористой среды при одноосном сжатии изображена на рис. 2. Процесс упругой деформации описывается уравнением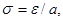 
а процесс упругопластической деформации материала после схлопывания пор – уравнением 
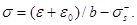Точка 
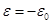соответствует моменту схлопывания пор. Приведенная диаграмма качественно соответствует результатам практических экспериментов по сжатию пористых металлов [2, 3].
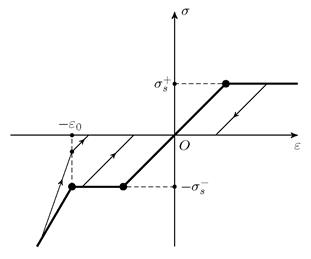
Рис. 2. Диаграмма связи между напряжением и деформацией
Используя реологическую схему, можно получить определяющие соотношения, которые совместно с уравнениями движения образуют замкнутую математическую модель пространственного динамического деформирования пористого металла [4, 5]:
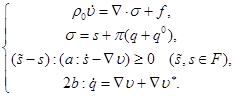
Здесь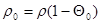 
– плотность; 
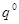– тензор, характеризующий пористость; 
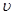– вектор скорости; 
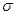– тензор напряжений; 
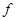– вектор объемных сил; 
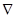– оператор Гамильтона; 
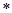обозначает сопряженный тензор. Используются механические характеристики пористого материала: тензоры упругой податливости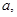 
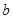и определяющие их модули сдвига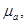 
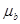и модули объемного сжатия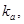 
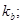предел текучести среды 
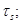начальная пористость 
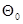– вычисленные для материала с малой пористостью в работе [6].
Рассмотрим продолжительное по времени мгновенно приложенное одноосное сжимающее воздействие, перпендикулярное плоской границе пористой среды. Модель описывает два варианта решения:
- схлопывание пор происходит на этапе упругой деформации, пластичность проявляется после уплотнения среды;
- уплотнение среды наступает после наступления пластичности.
Диаграммы связи между напряжением и деформацией для этих двух вариантов схематически изображены на рис. 3.
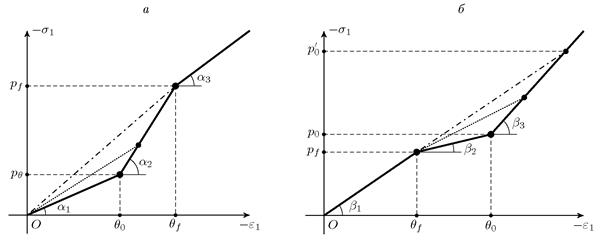
Рис. 3. Диаграммы одноосного сжатия:
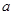– схлопывание пор на этапе упругой деформации,
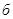– схлопывание пор после наступления пластичности
В первом вариант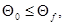е 
где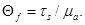 
Первое звено ломаной соответствует упругой деформации, и напряжения определяются по закону Гука:
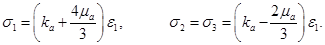(1)
Второе звено соответствует упругой деформации уплотненной среды, и напряжения определяются следующими уравнениями:
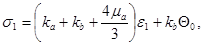
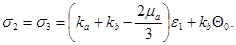
Третье звено – пластическое течение уплотненного материала. С учетом условия пластичности и закона упругого изменения объема, уравнения напряжений имеют следующий вид:
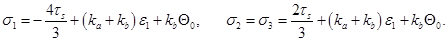(2)
Переход из состояния упругой деформации к пластическому течению непрерывен, поэтому наступление пластичности происходит при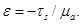 
Угловые коэффициенты каждого из звеньев равны:
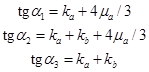, при этом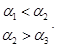 
Во втором варианте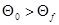 
первоначальная упругая деформация с напряжениями, вычисляемыми по формулам (1), сменяется пластическим течением пористого скелета. Напряжения на стадии пластической деформации определяются уравнениями:
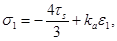
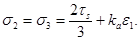
После этого происходит уплотнение среды. С учетом условия пластичности и закона упругого изменения объема напряжения находятся по формулам (2). Угловые коэффициенты каждого звена в этом случае равны:
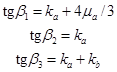, при этом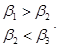 
Продольные ударные волны
Учитывая приведенные выше диаграммы связи между напряжением и деформацией и уравнения для вычисления напряжений и угловые коэффициенты звеньев ломаных, можно описать распространение продольных ударных волн в результате приложения к границе ненапряженного полупространства мгновенного постоянного давления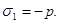 
Рассмотрим первый случай (рис. 3 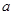). Если 
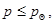где 
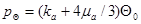– давление, при превышении которого происходит схлопывание пор, то в среде распространяется продольная упругая волна со скоростью 
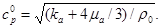Этой волне соответствует первое звено ломаной. Если 
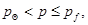где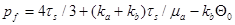 
– давление, при превышении которого происходит пластическое течение, то скорость волны равна 
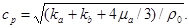Это упругая волна уплотнения, на которой происходит схлопывание пор. Ей соответствует пунктирная линия от начала координат до точки второго звена ломаной. Если 
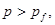то в среде будут распространяться две волны: первая – волна уплотнения со скоростью 
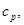соответствующей предельному напряжению 
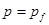(ей соответствует штрихпунктирная линия от начала координат до точки перехода к пластическому течению); вторая – пластическая ударная волна в уплотненной среде со скоростью 
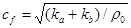(ей соответствует третье звено ломаной).
Во втором случае (рис. 3 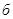) давление 
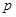может принимать значения из четырех различных диапазонов. Если 
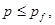где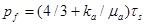 
– предельное упругое давление, при превышении которого начинается пластическое течение, то в среде распространяется продольная упругая волна со скоростью 
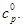Этой волне соответствует первое звено ломаной. Если 
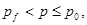где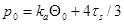 
– давление, при превышении которого происходит схлопывание пор, то в среде распространяются две волны: первая – упругий предвестник со скоростью 
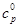(ей соответствует первое звено ломаной); вторая – пластическая ударная волна со скоростью 
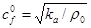(ей соответствует второе звено ломаной). Если 
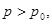то волны будет две, только следом за упругим предвестником будет распространяться волна пластического уплотнения со скоростью 
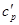, которая определяется из уравнения:
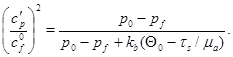
Этой волне соответствует пунктирная линия от точки перехода к пластическому течению до точки третьего звена ломаной. Возможен четвертый вариант: в высокопористой среде при выполнении условия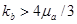 
и достижении давлением 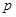значения 
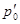волна пластического уплотнения догоняет упругий предвестник, а при 
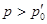возникает единственная волна со скоростью 
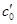, которая определяется из уравнения:
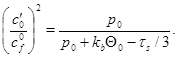
Этой волне соответствует штрихпунктирная линия от точки перехода к пластическому течению до точки третьего звена ломаной.
Литература:
1. Садовская О.В., Садовский В.М. Математическое моделирование в задачах механики сыпучих сред. – М.: Физматлит, 2008. – 368 с.
2. Banhart J., Baumeister J. Deformation Characteristics of Metal Foams // Journal of Materials Science, 1998. – V. 33, Iss. 6. – P. 1431–1440.
3. Ashby M.F. Plastic Deformation of Cellular Materials. Encyclopedia of Materials: Science and Technology (ISBN: 978-0-08-043152-9). Pergamon Press, 2001. – P. 7068–7071.
4. Садовский В.М., Садовская О.В., Лукьянов А.А. Радиальное расширение сферической и цилиндрической полостей в безграничной пористой среде // Прикладная механика и техническая физика, 2014. – Т. 55, № 4. – С. 160–173.
5. Sadovskii V.M., Sadovskaya O.V. Mathematical Modeling of a Metal Foam as an Elastic-Plastic Continuum with Changing Resistance // AIP Conf. Proc. 2015. – V. 1648. – P. 63005-1–63005-4 (DOI: 10.1063/1.4912863).
6. Золотухин А.В. Численное моделирование свойств пористых металлов // Материалы Всероссийской научно-практической конференции «Актуальные проблемы авиации и космонавтики». – Красноярск, СибГАУ, 2011. – Т. 1. – С. 138–139.
