Модель с распределенными параметрами для описания динамики процессов в растворах

Предложена модель с распределенными параметрами для описания динамики растворов соли. На ее базе произведен краткий анализ последствий внешних воздействий на раствор — неравномерное охлаждение. В модели учтены фазовые превращения — образование твердой фазы в жидком растворе соли. Разработана методика расчета, создано соответствующее программное средство. Выполнен ряд расчетов, представлен анализ достоверности результатов и определена область корректного использования модели. Содержится анализ выполненных ранее экспериментальных работ.

Ключевые слова: раствор соли, жидкая фаза, твердая фаза, кристаллизация, температура, концентрация, соль, растворитель, масса, объем.

В ходе моделирования стационарных и переходных процессов в различных отраслях техники возникает необходимость описания динамики концентрации раствора соли в связи с изменением теплофизицеских параметров. При этом рассматриваются как процессы с изменением только лишь концентрации раствора, так и с фазовыми переходами — образованием твердой фазы, выпадением кристаллов. В большинстве работ, посвященных данной проблеме, применяются точечные модели с сосредоточенными параметрами [1–6]. В последних работах особое внимание уделялось описанию кристаллизации, т. е. образованию твердой фазы [3–6].

В данной работе сделана попытка построения простейшей модели с распределёнными параметрами — температура, плотность, концентрация, фазовое состояние смеси,- а также определение границ ее корректного применения.

Предлагаемый алгоритм применения модели с распределенными параметрами (расчетная область разбита горизонтальными плоскостями на слои):

1.    построение «начального» стационарного состояния для раствора соли в сосуде с заданными параметрами — пространственное распределение необходимых физических величин и параметров задачи в соответствии с исходными данными;

2.    построение «конечного» состояния — пространственных распределений необходимых физических величин,- с учетом соответствующих граничных условий и с учетом параметров, полученных пункте 1. Методики построения «конечного» состояния соответствуют методикам для поиска стационарного состояния;

3.    далее из условия 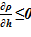 проверяется достоверность результатов для «конечного» состояния, т. е. обеспечение устойчивости решения. В случае соблюдения неравенства, полученное решение — «конечное» состояние,- является стационарным, достоверным, В противном случае «конечное» распределение параметров неустойчиво, требует учета процессов смешения в расчетном объеме или его частях.

Начнем со статической задачи — движение отсутствует, рассматриваемое вещество — раствор соли или двухфазная смесь (раствор соли и твердая фаза той же соли). Таким образом, «начальное» состояние есть постоянное распределение всех параметров раствора соли, включая температуру, во всем объеме.

В качестве «конечного» состояния раствора соли в вертикальном сосуде принимаем линейное распределением температуры в зависимости от высотной отметки — h. Новое распределение температуры влечёт за собой изменение плотности, концентрации, фазового состояния компонентов раствора соли. Далее производится проверка устойчивости решения. Естественным ограничением для корректного применения модели статики является изменение плотности от высоты 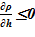, т. е. исключение причин для перемешивания между слоями — в верхних слоях должна находиться среда с меньшей плотностью, а в нижних слоях — наоборот, плотность раствора должна оставаться постоянной величиной либо возрастать.

Пусть рассматриваемый вертикальный сосуд имеет переменное сечение в зависимости от высотной отметки (Рис. 1.). Рассмотрим два состояния для раствора соли в сосуде. Как было сказано выше, именуем их «начальное» и «конечное».

Исходные данные для построения «начального» состояния следующие:

1)        масса соли, находящейся в сосуде в растворенном виде. Значение данной величины m_соли остается неизменной для расчетного объема. Возможны лишь изменения формы ее существования в «конечном» состоянии;

2)        задан уровень раствора в «начальном» состоянии — h_о;

3)        температура раствора в «начальном» состоянии неизменна по высоте — ;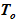

4)        геометрические данные для рассматриваемой области: зависимость площади поперечного сечения от высотной отметки — f(h). Последнее использовано для определения значения объема раствора соли в конкретном слое;

5)        геометрические параметры расчетной области. Объем состоит из набора слоев, разбиение произведено горизонтальными плоскостями с постоянным шагом по высотной отметке. Количество расчетных подобластей равно числу слоев — i_max.

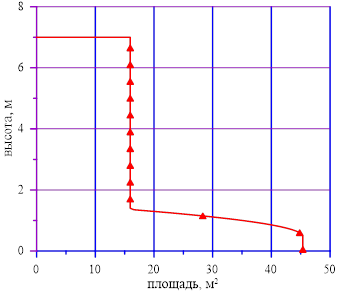
Рис. 1. Изменение поперечного сечения сосуда в зависимости от высотной отметки

На основе приведенных данных однозначно определяются основные параметры «начального» состояния: масса растворителя, концентрация и плотность раствора.

Для выполнения работы нам известны следующие физические зависимости:

1)        зависимость предельной концентрации раствора от температуры c’_пред = c’_пред(T) [7]. Для рассматриваемой в расчете соли и растворителя ;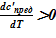

2)        термодинамические свойства растворителя 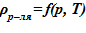 [8]. Для используемого растворителя соблюдается следующее — 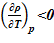. Это означает, что в случае линейного распределения температур в зависимости от высотной отметки 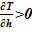, будет получено устойчивое статическое решение 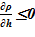, в котором исключено перемешивание, конвекция, а существует исключительно теплопроводность (между слоями и стенкой сосуда) и массообмен между фазами внутри слоя (например, осаждение кристаллов с образованием пористого слоя и т. д.);

3)        зависимость плотности раствора соли в зависимости от плотности растворителя и концентрации 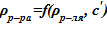 [9];

4)        плотность твердой фазы (кристаллов) постулируется неизменной 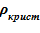=const [7];

5)        теплота фазового перехода (кристаллизации соли) в растворе равна нулю;

6)        постулируется, что, в случае образования твердой фазы, выпадение последней происходит на стенках, т. е. весовой столб в этом процессе по–прежнему определяется плотностью жидкого раствора соли — исключительно жидкостью.

Граничные условия для построения «конечного» состояния:

1)        задано линейное распределение температуры по высоте (или номеру слоя) в «конечном» состоянии;

2)        содержание соли и растворителя для каждой подобласти (в слое) остается неизменным — определяется в ходе построения «начального» состояния. Возможно лишь изменение формы существования соли — в виде раствора соли или в виде двухфазной смеси (жидкий раствор соли и твердая фаза — кристаллы).

Поиск решения для «конечного» состояния разбит на три части:

1)        построение «начального» состояния на основе исходных данных (приведены выше) — масса растворителя и раствора, плотность раствора, распределения по слоям всех необходимых параметров;

2)        расчет «конечного» состояния, соответствующего изменившемуся распределению температур (см. выше). На данном этапе «постулируется» новое статическое состояние параметров раствора — массы растворителя/соли в каждом из слоев неизменны,- а может происходить изменение плотности/концентрации/фазового состояния раствора соли из-за изменения температуры в слое. Изменяется, соответственно, и объем среды в слоях;

3)        анализ устойчивости полученного решения, делаются выводы о возможности принятия решения в качестве конечного статического распределения либо неустойчивого. В последнем случае понадобится учет процессов смешения в расчетном объеме или его частях.

Как упомянуто выше, в модели слоев расчетная область от минимальной высотной отметки до максимальной (известная величина для «начального» состояния) разбита горизонтальными плоскостями с постоянным шагом по высоте на расчетные подобласти, слои — sub–volumes. Поперечное сечение расчетного объема изменяется в зависимости от высотной отметки 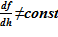. Решение строится в координатах Лагранжа — для каждой из подобластей (слоя) sub–volumes фиксируются переменные, связанные с массовыми значениями, а именно:

-          масса растворителя ;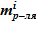

-          масса соли 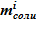. Раствор соли в «конечном» состоянии может претерпевать изменения агрегатного состояния, т. е. образование двухфазной смеси — твёрдой фазы (кристаллов) и раствора соли.

Изменение теплофизических параметров в «конечном» состоянии (давления p, температурыT), — приводит к изменению плотности растворителя и раствора. Это учтено в модели, т. е. значения объемов слоев sub–volumes в «конечном» состоянии отличаются от начальных. Нижняя отметка уровня остается постоянной — 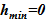 м, а верхняя отметка, соответственно, претерпевает изменения — .

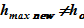В построении «начального» состояния задействованы следующие данные:

-          число слоев в расчетной области неизменно (известный параметр);

-          давление среды p_о=const(h);

-          температура T_о=const(h);

-          верхняя высотная отметка для раствора h_о;

-          начальная масса соли m_соли, находящейся в виде раствора;

-          геометрические данные для рассматриваемой области — f(h), .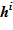

В результате получаем картину — «начальное» состояние раствора соли в расчетной области, для каждого слоя:

-          концентрация раствора c’=const(h);

-          плотность растворителя и раствора ;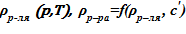

-          масса растворителя 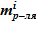 и соли в растворе  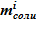для каждого слоя — sub–volumes.

Для построения решения для «конечного» состояния используются следующие данные:

-          число слоев в расчетной области неизменно;

-          давление среды p= p_о (для простоты изложения);

-          распределение температуры в зависимости от номера слоя T≠const(h) — задано в граничных условиях. В нашем примере для простоты изложения использована линейная зависимость.

Искомые величины для каждого слоя — sub–volumes в «конечном» состоянии:

-          объем раствора ;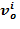

-          новые высотные отметки для слоев раствора ;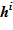

-          масса растворителя 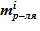– неизменна;

-          масса соли 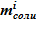 в каждом слое неизменна, требуется уточнение нового агрегатного состояния для жидкого раствора соли — это по-прежнему раствор соли или двухфазная смесь (твердая фаза и раствор соли);

-          текущая и предельная концентрации раствора, масса кристаллов соли.

Для устойчивого решения — стационарного, — не предусмотрено перемешивание, наличие конвекции в «конечном» состоянии. Именно поэтому в «конечном» состоянии принята зависимость 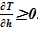 В расчете будем использовать линейную интерполяцию температуры в зависимости от номеров слоев  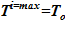и 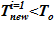. Данное распределение температуры по высоте аппарата с подводом тепла широко распространено в различных областях техники, в том числе, и в химических технологиях [1, 2].

Ι. Алгоритм построения «начального» состояния

1.    Расчет плотности растворителя для известных параметров — .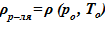

2.    Вычисление начального значения рабочего объема, занимаемого раствором — .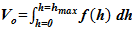

3.    Определение предельной концентрации, соответствующей начальной температуре — .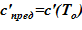

4.    Далее следует алгоритм «метод деления отрезка пополам»: минимальная концентрация раствора 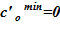 и максимальная концентрация — .

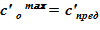5.    Вычисление среднего значения для концентрации раствора .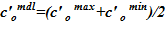

6.    Определение значения плотности раствора .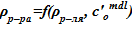

7.    Вычисление массы раствора для расчетного объема .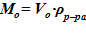

8.    Определение соответствующей массы соли .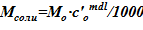

9.    Сравниваем полученное значение массы соли с заданным значением и, в случае существенной разницы, корректируем соответствующее значение для 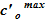 или 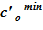, после чего повторяем алгоритм с пункта 5. Если разница между  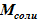и заданной величиной приемлема, то заканчиваем итеративный алгоритм — найдено начальное значение для концентрации раствора в расчетном объеме .

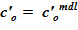10.     Вычисление плотности раствора .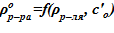

11.     Для каждого из слоев sub–volumes производится вычисление необходимых величин:

11.1          значение объема ;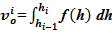

11.2          массы раствора ;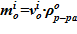

11.3          массы соли в растворе ;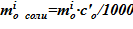

11.4          массы растворителя в растворе .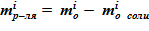

ΙΙ. Алгоритм построения «конечного» состояния

Согласно граничным условиям и допущениям в рассматриваемой задаче давление в расчетном объёме остается неизменным, распределение температур — линейная интерполяция от T_{new max} = T_o(i=max) до T_{new min} = T_min(i=1).

Решение строится по слоям — «снизу–вверх», т. к. в известно лишь положение нижнего слоя в «конечном» состоянии.

Для каждого слоя по температуре 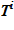 вычисляется 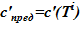. Если 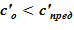, то «конечном» состоянии в данном слое находится раствор и применяется соответствующий алгоритм поиска. В противном случае, для  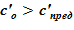используется алгоритм поиска параметров двухфазной смеси — жидкого раствора и твердой фазы, кристаллов.

ΙΙ.1 Алгоритм построения «конечного» состояния для раствора

В рассматриваемом слое — sub–volumes отсутствуют массовые превращения, концентрация неизменна — .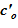

1.    Определение значения плотности растворителя при соответствующем значении температуры Tⁱ и давлении p в слое — .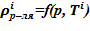

2.    Вычисление плотности раствора и .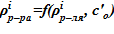

3.    Определение значения объема для слоя .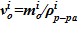

4.    Далее, по значению 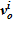, вычисляется высотная отметка для данного слоя  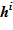с учетом известной высотной отметки предыдущего слоя  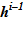и геометрических данных рассматриваемой области f(h). Алгоритм поиска высотных отметок для конкретного sub‑volumes зависит от геометрии расчетного объема, он не представлен, т. к. это задача, зависящая от геометрии расчетного объема (в представленной задаче — см. Рис. 1.).

ΙΙ.2 Алгоритм построения «конечного» состояния для двухфазной смеси

1.    Исходное утверждение — состояние среды двухфазное, т. е. смесь жидкого раствора при предельной концентрации и твердой фазы, кристаллов.

2.    Масса растворителя в слое неизменна, а концентрация раствора равна предельной концентрации раствора 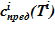 при соответствующей температуре раствора в слое.

3.    Вычисление массы соли для i–ого слоя, находящейся в растворенном виде, следующим образом .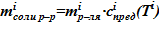

4.    Определение массы раствора для i–ого слоя .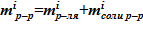

5.    Масса соли в составе твердой фазы, в виде кристаллов, соответственно — 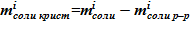 для i–ого слоя.

6.    Объем твердой фазы 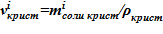 для i–ого слоя.

7.    Объем раствора раствора — 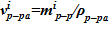, — в i–ом слое.

8.    Общий объем среды в текущем слое .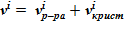

9.    По значению высотной отметки предыдущего слоя 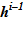, известному значению объема vⁱ и геометрическим данным определяется положение верхней границы  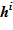для текущего слоя. Верхняя граница последнего слоя есть граница расчетного объема в новом состоянии.

Рассмотрим реализацию предложенной методики и определим область ее корректного использования. Заодно проанализируем возможные физические процессы и явления в области с неравномерным распределением температуры по высотной отметке.

Задача 1. «Начальное» состояние — температура раствора одинакова и составляет 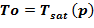=133 ^oC_. В «конечном» состоянии на верхней границе температура остается неизменной T_o, а температура в нижнем слое  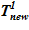=80 ^оС снижается до значений, при которых не достигаются условия возникновения кристаллизации 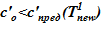. Напоминаем, распределение температур в «конечном» состоянии — линейное распределение по номерам слоев. Общее число слоев — 140.

Результаты расчета представлены на рисунках 2–7.

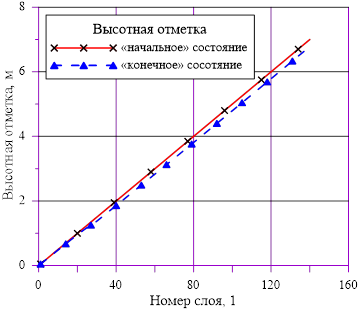
Рис. 2. Вертикальные координаты для слоев

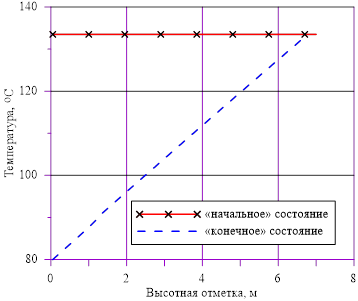
Рис. 3. Распределение температуры по высоте

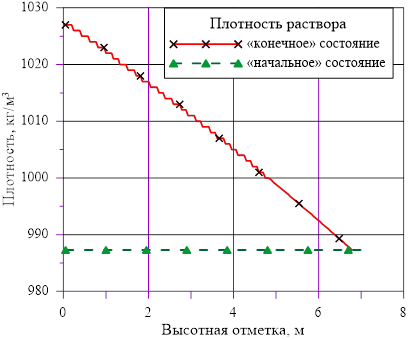
Рис. 4. Изменение плотности раствора по высоте

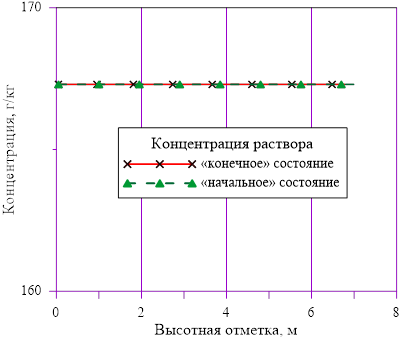
Рис. 5. Зависимость концентрации раствора от высоты

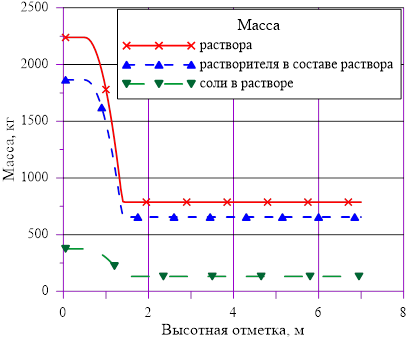
Рис. 6. Распределения основных величин по высоте в «начальном» состоянии

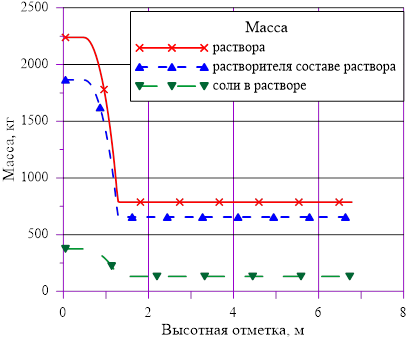
Рис. 7. Распределения основных величин по высоте в «конечном» состоянии

Заключение по результатам задачи 1.

Линейное распределение температуры в слоях расчетного объёма в «конечном» состоянии привело к близкому к линейному распределению плотности раствора. Это решение соответствует статическому решению, удовлетворяющему условиям устойчивости 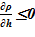. Причин для возникновения опрокидывания столба раствора, перемешивания, конвекции и т. д. в этом случае не возникает. В каждом слое массы основных компонентов (растворителя и соли) и их агрегатное состояние (жидкий раствор соли) остались неизменными, из чего следует — концентрация раствора соли во всей расчетной области осталась равной исходному значению. Решение, исходя из выше сказанного, не противоречит общим представлениям о возможности применения модели слоев для описания неравномерного по высоте поля температур  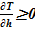без фазовых переходов, т. е. без образования твердой фазы. Изменение плотности раствора (увеличение из-за снижения температуры) привело к снижению верхней отметки уровня в «конечном» состоянии из-за снижения общего объема раствора в расчетной области.

Задача 2. «Начальное» состояние — температура по высоте одинакова и составляет 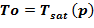=133 ^oC — совпадает с задачей 1. В «конечном» состоянии температура раствора соли на верхней границе остается неизменной T_o, а температура среды в нижнем слое снижается  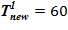^оС. Для «конечного» состояния в области дна данной температуре соответствуют предельные концентрации раствора меньшие, чем начальные в расчетном объеме. Именно этот факт, например, для нижнего слоя есть причина возникновения двухфазной смеси — раствора соли с предельной концентрацией  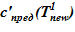и твердой фазы. Принимаем, по-прежнему, для простоты линейное распределение температур по номерам слоев, .

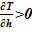Основные результаты представлены на рисунках 8–16.

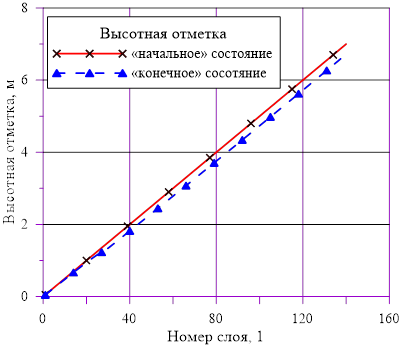
Рис. 8. Вертикальные координаты для слоев

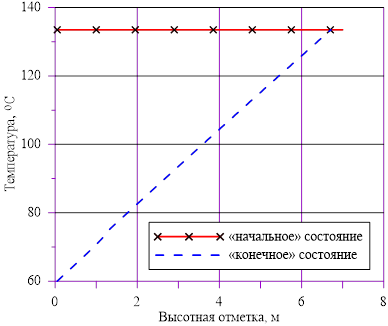
Рис. 9. Распределение температуры по высоте

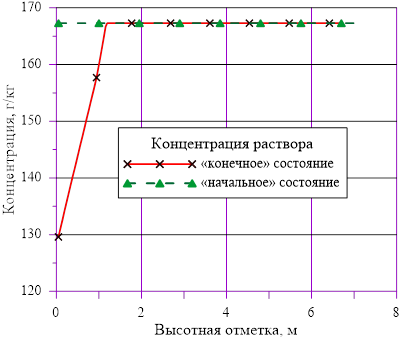
Рис. 10. Изменение концентрации в слоях по высоте

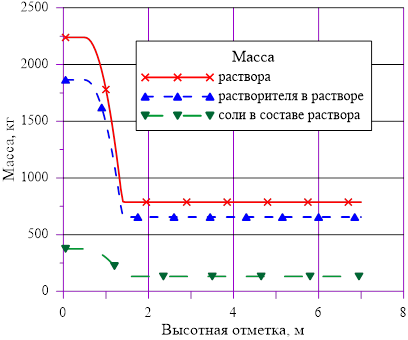
Рис. 11. «Начальное» распределение компонентов раствора

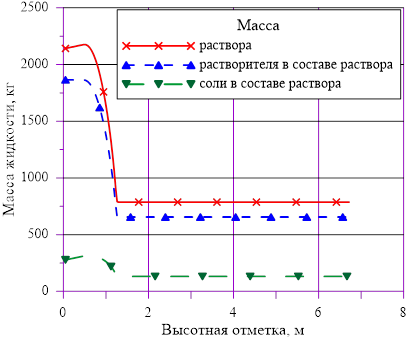
Рис. 12. «Конечное» распределение компонентов раствора

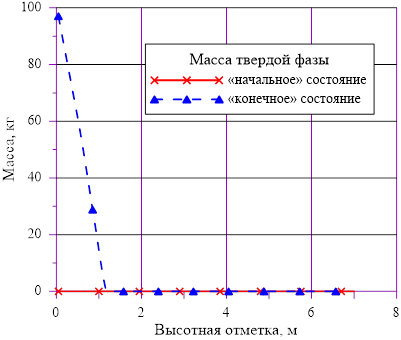
Рис. 13. Распределение твердой фазы по высотной отметке

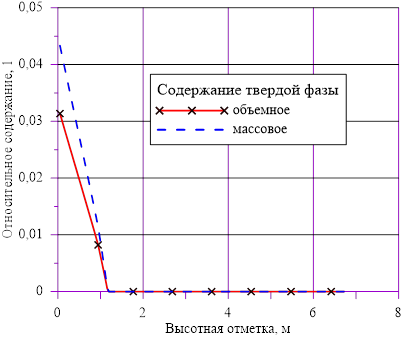
Рис. 14. Изменение относительного содержания твердой фазы по высотной отметки в «конечном» состоянии

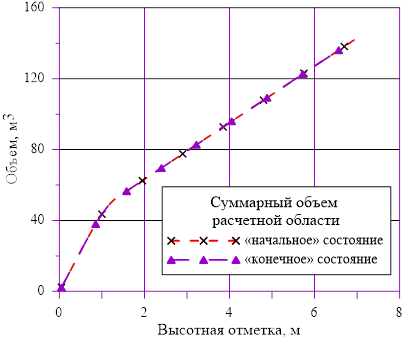
Рис. 15. Изменение объёма в зависимости от высотной отметки

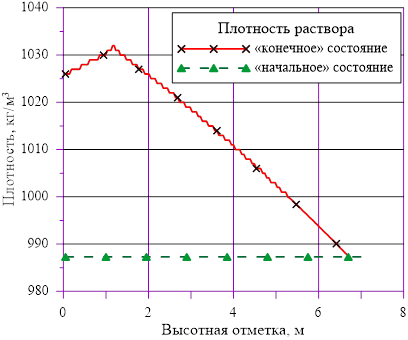
Рис. 16. Изменение плотности раствора в зависимости от высотной отметки

Заключение по результатам задачи 2.

В расчете использована соль и растворитель, образующих раствор с увеличением предельной концентрации с ростом температуры. Концентрация в «начальном» состоянии была ниже, чем значение предельной концентрации при начальной температуре. В «конечном» состоянии снижение температуры в нижних слоях расчетного объёма привело к тому, что в содержащемся в них растворе начальная концентрация c’₀ стала превышать значения предельных значений концентраций c’₀ > c’_пред(T). Это означает, что концентрация раствора в нижних слоях назначается равной предельной концентрации, соответствующей текущему значению температуры в «конечном» состоянии. При этом образуется двухфазная смесь, в которой сосуществуют два компонента — раствор с предельной концентрацией соли, соответствующей значению температуры, и твердой фазы, т. е. кристаллов.

Данное решение для задачи охлаждения «столба» раствора соли с градиентом температур и наличием фазового перехода является неустойчивым, т. к. плотность раствора в нижних слоях (см. Рис. 16.), где появился раствор с предельными концентрациями, стала ниже аналогичной величины в расположенных выше слоях 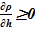. Это означает, что неизбежно возникают причины для перемешивания и возникновения иного конечного распределения температур и концентрации раствора. Решение с образованием твердой фазы только лишь в области дна и только лишь из–за снижения температуры в сосуде с раствором, первоначально заполненным раствором с постоянной концентрацией, является неустойчивым для использованных в нашем примере веществ — растворителя и соли.

Для других растворов солей — иного растворителя и соли, с учетом их теплофизических свойств и зависимости предельной концентрации от температуры, — возможность возникновения описанного явления следует учитывать и принять во внимание.

В рамках определенной авторами задачи одну из целей исследования можно считать достигнутой. Определены границы статического решения для охлаждения столба раствора соли, не требующие дальнейших доработок. Получены условия существования границы неустойчивого решения при образовании двухфазной смеси, которые требуют рассмотрения и учета перемешивания при снижения температуры в нижних слоях столба с жидким раствором соли.

Замечание 1 Выявленный эффект есть причина для перемешивания и выравнивания температур и концентраций раствора — однородности поля величин, — первоначально в нижней части для нашей «лабораторной» задачи. Если в следующем примере «новое» значение температуры в области дна будет ниже, чем 60 ^оС, то это приведет к росту протяженности области, в которой 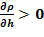, т. е. к большей протяженности зоны с неустойчивым решением.

Замечание 2 В случае реальных задач с динамикой растворов соли и распределенными параметрами, представленный в публикации механизм может быть только одним из слагаемых в наборе процессов, обеспечивающих перемешивание раствора соли.

Замечание 3 Существует вероятность, что наглядно продемонстрированное неустойчивое решение может приводить к перемешиванию, препятствуя кристаллизации, по–видимому, вплоть до образования однородного раствора с предельными концентрациями соли во всем сосуде. Данный факт может стать одной из возможных причин для использования в целом ряде задач, связанных с образованием твердой фазы, точечных моделей с сосредоточенными параметрами.

Задача 3

Обсудим результаты экспериментальной работы на близкую тему. Ранее авторам не встречалось простое объяснение результатов, затрагивающих вопросы кристаллизации, представленных в работе [10]. В экспериментах в большинстве случаев зафиксировано образование твердой фазы в области дистанционирующих решеток в верхней части обогреваемого участка, что указывало, по–видимому, на хорошее перемешивание раствора как по высоте обогреваемого участка, так и во входном участке. где «должен» находиться раствор с меньшей температурой. В части опытов с образованием твердой фазы место отложения зафиксированы над смачиваемой поверхностью. Перечисленное указывает на конкретную роль перемешивания раствора по высоте рабочего участка, роль паро–капельного уноса, уноса соли в растворенном виде с паром.

Рассмотрим экспериментальную установку с точки зрения модели слоев. Условно разбиваем верхнюю камеру смешения (ВКС), рабочий участок и нижнюю камеру смешения (НКС) стенда, сверху вниз, на три слоя, три подобласти: «зона интенсивного кипения, включая ВКС»; «зона подвода тепла без образования паровой фазы»; «входной участок и НКС».

Верхний слой. В зоне заполненной паром, зоне интенсивного кипения, благодаря увеличению расхода пара с ростом высотной отметки, для пароводяной смеси соблюдается 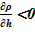. Последнее означает, что данное распределение устойчиво, причины для его «разрушения» отсутствуют, несмотря на интенсивные процессы перемешивания в самом слое — паро-капельного слоя в ВКС, образование и всплывание паровых пузырей в зоне кипения вверх, что вызывает колебательное движение насыщенной жидкости и положения «набухшего» уровня двухфазной смеси. В заключительной стадии экспериментов [10], согласно оценкам, достигались концентрации раствора соли, близкие к предельным c’₀ = c’_пред. Им соответствует плотность раствора соли при температуре насыщения и предельной концентрации 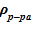=1053 кг/м³. Наличие пара в парожидкостной смеси приводит к снижению реального значения плотности, по сравнению с указанным выше .

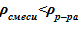Средний слой. В зоне подвода тепла без образования паровой фазы происходит прогрев поступающего в рабочий участок раствора соли до температуры насыщения. Благодаря значительным конвективным течениям, перемешивание связано не только с обменом тепла, но и со смешением растворов разных концентраций — поступающего в НКС (минимальная концентрация раствора соли, минимальная температура) и расположенного в зоне кипения (максимальная температура и, соответствующая ей максимальная концентрация раствора — предельная c’₀ > c’_пред). Для простоты изложения принимаем, что в зоне подвода тепла без образования паровой фазы плотность жидкого раствора соответствует значению при предельной концентрации 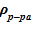=1053 кг/м³.

Тогда для двух верхних слоев имеется устойчивое, не противоречащее законам статики, распределение 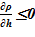 плотность снижается или остается постоянной с ростом высотной отметки. Это распределение безусловно устойчиво.

Нижний слой. В эксперименте в НКС поступал раствор при температуре 40 ^оС и малой концентрации раствора 16–40 г/кг [10] c’₀ << c’_пред. Соответствующая плотность раствора соли равна 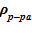=997,3 кг/м³, т. е. плотность раствора в нижнем слое ниже, чем аналогичное значение для расположенного выше среднего слоя. Указанные значения плотности не соответствуют устойчивому статическому решению — над «легкой» жидкостью расположена «тяжелая». Этот факт неустойчивого решения, вызывает интенсивное перемешивание раствора, как минимум, для двух нижних слоев: «входной участок и НКС» и «зона подвода тепла без образования паровой фазы».

Выводы

Построена модель для воспроизведения процессов в «столбе» раствора соли с распределенными по высоте параметрами, разработано программное средство, результаты расчетов представлены в публикации.

В настоящей работе рассмотрена статическая модель для слоистой структуры солевого раствора в столбе — среда в состоянии покоя. Реальная картина в экспериментальной установке с подводом тепла, где имеются неодномерные распределения физических параметров и многомерные конвективные течения с перемешиванием и парообразованием, все намного сложнее. Но предложенная простейшая модель полезна для объяснений процессов, протекающих в экспериментальной установке, а также в промышленных объектах с растворами солей.

Применение моделей слоев способствует пониманию динамических процессов в растворах солей, а ее использование является одним из средств для анализа явлений в них.

Актуальность создания моделей для описания динамики концентрации раствора соли подтверждается рядом публикаций [1, 2, 11]. Это означает, что приведенный материал может использоваться при разработке и обосновании проектно–конструкторских решений для различных технологических систем и ряда технических объектов.

Литература:

1.    Касаткин А. Г. Основные процессы и аппараты химической технологии. М.: Химия, 1971, 784 с.

2.    Гельперин Н. И. Основные процессы и аппараты химической технологии. М.: Химия, 1981, 812 с.

3.    Шмаль И. И. Аналитические оценки для процесса кристаллизации // Молодой ученый. 2013. № 7 (54). С. 30–31.

4.    Шмаль И. И. Метод расчета нестационарных изменений концентрации в выпарных установках // Молодой ученый. 2013. № 8 (55). С. 42–44.

5.    Шмаль И. И. Проблемы моделирования кристаллизации // Молодой ученый. 2013. № 8 (55). С. 44–47.

6.    Шмаль И. И., Иванов М. А. Расчет динамики накопления и кристаллизации соли в выпарном аппарате с переменными параметрами в спускной циркуляционной трубе // Молодой ученый. 2014. № 10 (69). С. 54–61.

7.    Справочник химика. В 5 т.: Т. 4. Справочник химика. В 5 т.: Т. 3. Редакционная коллегия Никольский Б. П. (гл. редактор) и др. — М., Химия: 1965, 1168 с.

8.    Александров А. А., Григорьев Б. А. Таблицы теплофизических свойств воды и водяного пара. Справочник. — М., МЭИ, 1999. 168 с.

9.    Jari Tuumanen. Thermal–Hydraulic Studies on the Safety of VVER–440 type Nuclear Power Plants. Thesis for the Doctor Degree of Technology. Lappeenranta, Finland, 1994.

10.              Балашов С. М., Виденеев Е. Н., Нигматулин Б. И. Влияние борной кислоты на теплогидравлические характеристики частично осушенной активной зоны. // Теплоэнергетика. 1992. № 9. С. 43–47.

11.              Логвинов С. А., Безруков Ю. А. Драгунов Ю. Г. Экспериментальное обоснование теплогидравлической надежности реакторов ВВЭР. — М., ИКЦ «Академкнига», 2004. 255 с.