В данной статье рассмотрены статически неопределимые конструкции к которым можно отнести ряд характерных особенностей: в статически неопределимых системах возникают меньшие внутренние усилия, что определяет их экономичность по сравнению со статически определимыми системами при одинаковых внешних нагрузках; при расчете статически неопределимых систем необходимо заранее выбрать материал конструкции, так как необходимо знать его модули упругости.
Ключевые слова: статически неопределимых систем, стержневая система, поперечные сечения, конструкция, удельный вес, продольные силы.
Статически неопределимой системой называется такая система, которая не может быть рассчитана при помощи одних только уравнений статики, так как имеет лишние связи. Иными словами, если в данной системе число неизвестных усилий в опорных стержнях (опорных реакциях) и число неизвестных усилий в элементах системы (продольных и поперечных сил, моментов) превышает число уравнений равновесия статики, то система статически неопределима.
Характерной особенностью статически неопределимых систем (в отличие от статически определимых) является то, что распределение усилий в них зависит не только от внешних сил, но и от соотношений между поперечными размерами отдельных элементов. Если элементы системы изготовлены из различных материалов, то распределение усилий зависит также от модулей упругости этих материалов [1]. Для расчета таких систем составляют дополнительные уравнения, учитывающие деформации системы. Для этого выполним анализ ее схемы. Анализ необходим, прежде всего, для того, чтобы установить степень статической неопределимости. Степень статической неопределимости равна числу так называемых лишних связей, удаление которых превращает статически неопределимую систему в определимую геометрически неизменяемую систему. Изображенная на рисунок 1, а прямоугольная замкнутая рама является системой трижды статически неопределимой, так как для превращения ее в статически определимую необходимо, например, перерезать один из ее элементов рисунок 1,б и тем самым устранить три лишние внутренние связи. Реакциями этих внутренних связей являются: продольная сила N, поперечная сила Q и изгибающий момент M, действующие в месте разреза. Эти реакции при помощи уравнений статики не могут быть найдены. В аналогичных условиях в смысле статической неопределимости находится любая система, представляющая замкнутый контур, который всегда трижды статически неопределим [2].
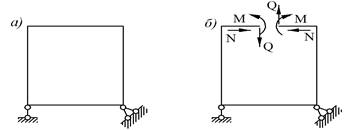
Рис. 1. Пример трижды статически неопределимой сиcтемы
В рамной конструкции, представленной на рисунок 2, а, верхний контур снабжен шарниром; в разрезе, проведенном по этому шарниру, действуют только два внутренних усилия: N и Q (рис. 2, б). Такой контур дважды статически неопределим. Если рассматривать всю систему (рис. 2, а) в целом, то она будет пять раз статически неопределима, так как нижний контур этой рамы замкнутый и, следовательно, неопределим трижды. Система, освобожденная от внутренних лишних связей, в данном случае будет состоять из двух защемленных внизу стержней с горизонтальными консолями (рис. 2, б). Необходимо заметить, что исключение лишних связей для превращения одной и той же статически неопределимой конструкции в статически определимую может быть произведено различными способами, однако число отбрасываемых связей всегда будет одно и то же.
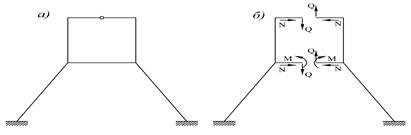
Рис. 2. Пример 5 раз статически неопределимой сиcтемы
На примере рамы, изображенной на рисунок 2, а, выясним еще одно обстоятельство. В системах, содержащих лишние опорные связи, степень внешней и внутренней статической неопределимости зависит от способа удаления связей системы. Например, при первом варианте удаления связей по рисунок 2, б конструкция может рассматриваться как пять раз внутренне статически неопределимая. При втором же варианте рисунок 3 она три раза внутренне и два раза внешне неопределима. Очевидно, деление неопределимости на две категории — внешнюю и внутреннюю — имеет смысл только при определенном способе удаления связей. Такое деление, не увязанное со способом удаления связей, лишено смысла.
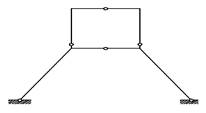
Рис. 3. Основная система для три раза внутренне и два раза внешне неопределимой конструкции
Включение шарнира в узел рамы, в котором сходятся два стержня, или же постановка его в любое место на оси стержня нарушит (снимет) одну связь и снижает общую степень статически неопределимости системы на единицу. Такой шарнир будем назвать одинарным или простым.
При удалении связей системы необходимо следить за тем, чтобы получаемая конструкция была геометрически неизменяема. С этой точки зрения в раме, представленной на рисунок 4, а, имеющей одно лишнее опорное закрепление, было бы ошибочным удаление вертикального стержня рисунок 4, б, так как оставшиеся при этом три опорных стержня пересекались бы в одной точке и, следовательно, не могли бы препятствовать повороту рамы вокруг этой точки. Определить усилия в этих стержнях из уравнений статики было бы невозможно, так как для сил, пересекающихся в одной точке, статика дает всего два уравнения. С точки зрения геометрической неизменяемости полученная система является мгновенно изменяемой. Правильный вариант удаления лишнего стержня указан на рисунок 4, в.
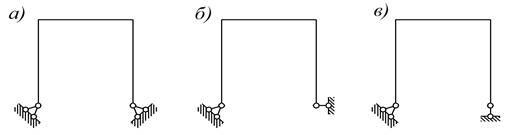
Рис. 4. Пример рамы имеющей одно лишнее опорное закрепление и варианты удаления лишнего стрежня
Дадим геометрическое толкование понятия статической неопределимости системы. Если в статически определимой системе (например, в ферме или трехшарнирной арке) устранить какую-либо внешнюю или внутреннюю связь, то она превратится в геометрически изменяемую систему. Следовательно, статически определимая конструкция содержит в своем составе такое количество связей, которое является минимально необходимым для обеспечения ее геометрической неизменяемости. Связи избыточные (сверх этого количества) порождают статическую неопределимость конструкции. Однако не каждая связь неопределимой конструкции может быть принята за лишнюю, так как удаление некоторых связей может сделать конструкцию изменяемой. В этом смысле все связи проф. И. М. Рабинович делит на две категории: абсолютно необходимые и условно необходимые. К первой категории принадлежат те связи, удаление которых из статически неопределимой конструкции делает ее геометрически изменяемой рисунок 4, б. Например, на рисунке 4, а такими связями являются вертикальные опорные стержни. Удаление любого из них делает систему мгновенно изменяемой. Ко второй категории относятся те связи, удаление которых не делает систему геометрически изменяемой, например горизонтальные опорные стержни системы, изображенной на рисунке 4, в. Интересно отметить, что усилия, возникающие в абсолютно необходимых связях статически неопределимой конструкции, находятся из условий статики. Наоборот, усилия в условно необходимых связях требуют для своего разыскания изучения деформаций конструкции [3]. Отброшенные связи заменяются в основной системе внешними, вначале неизвестными силами, приложенными по направлениям отброшенных связей, причем значения этих сил подбираются из условий отсутствия перемещений по направлениям отброшенных связей. Полученная таким образом система уравнений называется системой канонических уравнений метода сил [4]. При расчете статически неопределимых систем по методу перемещений за искомые величины принимаются те перемещения, через которые можно будет определить величины внутренних усилий в любом произвольном сечении. Кроме того, пренебрегают различием длин элементов заданной системы до и после нагружения системы. Известно, что для определения изгибающего момента в произвольном сечении заданного стержня необходимо знать величины поворотов в концевых сечениях и относительные линейные смещения концов стержня друг относительно друга.
Основная система получается из заданной путем введения новых жестких связей, то неизвестными являются перемещения по направлениям этих связей, а условиями для составления уравнений — условия отсутствия реактивных сил во введенных связях. Таким путем получают канонические уравнения метода перемещений. Применяется также смешанный метод, в котором основная система получается из заданной исключением одних жестких связей и введением других. Таким способом достигается эквивалентность заданной и основной систем как в отношении внутренних сил, так и в отношении перемещений узлов, а следовательно, и деформаций. Недостатком введения основной системы является необходимость производить расчет ее несколько раз: на действие заданной нагрузки и на действие каждого неизвестного усилия в отброшенных связях или на действие каждого неизвестного перемещения по направлениям введенных связей. Существенные затруднения возникают также при вычислениях коэффициентов канонических уравнений, а также их свободных членов.
С развитием машинно-вычислительной техники на первое место выдвинулись требования автоматизации расчета и максимального упрощения составления исходных данных для машины. С этой точки зрения некоторые из классических методов расчета статически неопределимых систем оказались недостаточно удобными.
Литература:
1. Саргсян А. Е., Демченко А. Т., Дворянчиков Н. В., Джиничвелашвили Г. А. Строительная механика. — Москва: Высшая школа, 2000.
2. Баженов В. А., Оробей В. Ф., Дащенко А. Ф., Коломиец Л. В. Строительная механика. — Одесса: Астропринт, 2001.
3. Галеев Э. М., Тихомиров В. М. Оптимизация: теория, примеры, задачи. — Москва: Эдиториал УРСС, 2000.
4. Баженов В. А., Дащенко А. Ф., Оробей В. Ф., Сурьянов Н. Г. Численные методы в механике. — Одесса: Астропринт, 2004.
5. Дыховичный Ю. А., Максименко В. А. Оптимальное строительное проектирование. — Москва: Стройиздат, 1990.







