Рассматриваются варианты методов расчёта полу бесконечных стержней, которые могут являться моделями различных строительных конструкций (например, свай в грунте).
Ключевые слова: методы расчёта, строительные конструкции, полу бесконечный стержень, упругие связи, жёсткость.
Усовершенствование методов расчёта и создание (совершенствование) различных строительных конструкций является актуальной задачей. В Пензенском государственном университете архитектуры на протяжении долгого времени активно занимаются (на различных кафедрах) решением данных проблем, с результатами исследований можно познакомится в работах [1…5].
Полубесконечный стержень постоянной жесткости EF нагружен на конце силой P (рис. а). Упругие распределенные связи, прикрепляющие его к жесткому основанию, имеют постоянный коэффициент жесткости k (k — интенсивность суммарной распределенной реакции в связях от единичного смещения поперечных сечений стержня относительно основания). Получить зависимость распределения продольных сил по длине стержня и вычислить перемещение его концевого сечения.
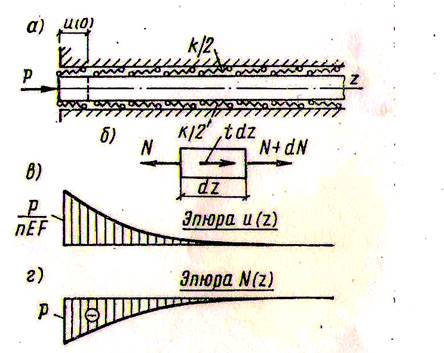
Рис.1 Полубесконечный стержень
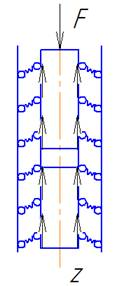
Рис.2 Модель сваи в грунте
Эта система статически неопределимая. Так как неизвестной является функция N(z) или u(z), то для ее определения необходимо составить не алгебраическое, а дифференциальное уравнение. Воспользуемся дифференциальными зависимостями для стержня при растяжении (сжатии):
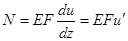 ; (а)
; (а)
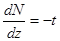 , (б)
, (б)
где u — продольное перемещение сечения стержня; t — интенсивность суммарной продольной распределенной нагрузки. В общем случае при наличии внешней нагрузки q и упругих связей значение t состоит из двух слагаемых: 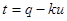 . Дифференцируя выражение (а) и используя соотношение (б), получим дифференциальное уравнение равновесия, выраженное через перемещения u:
. Дифференцируя выражение (а) и используя соотношение (б), получим дифференциальное уравнение равновесия, выраженное через перемещения u:
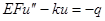 . (в)
. (в)
В нашем случае q=0. Поэтому уравнение (в) запишется так:
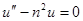 ,
,
где 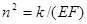 . Его общий интеграл имеет вид
. Его общий интеграл имеет вид 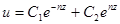 . Так как при
. Так как при 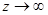 ,
, 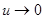 , то
, то 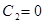 . Значение
. Значение 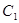 найдем из условия, что при
найдем из условия, что при 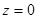 выражение
выражение 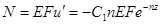 должно быть равно (-P); отсюда
должно быть равно (-P); отсюда 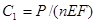 . Тогда искомые зависимости будут:
. Тогда искомые зависимости будут: 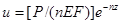 и
и 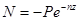 . Их графики изображены на рис. в и г. При
. Их графики изображены на рис. в и г. При 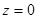 перемещение
перемещение 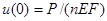 .
.
В случаи если, температура стержня, рассмотренного (выше), изменяется на 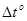 . Получить выражения для перемещений и продольных сил; коэффициент температурного расширения
. Получить выражения для перемещений и продольных сил; коэффициент температурного расширения 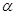 .
.
Суммарное состояние стержня можно получить путем наложения двух состояний: первого — при 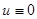 и, следовательно,
и, следовательно, 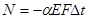 ; второго — от действия нагрузки, обеспечивающей первое состояние и имеющей обратный знак. В данном случае это будет действие растягивающей силы, приложенной к концу стержня:
; второго — от действия нагрузки, обеспечивающей первое состояние и имеющей обратный знак. В данном случае это будет действие растягивающей силы, приложенной к концу стержня: 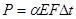 .
.
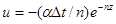 ;
; 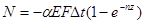 .
.
Таким образом мы получили зависимость распределения продольных сил по длине стержня и вычислить перемещение его концевого сечения, плюс к этому рассмотрели возможность изменения температуры стержня.
Предложим методы по распределению нагрузок и проектированию конструкций (в т. ч. машиностроительных):
а) простые конструкции необходимо проектировать с минимальным количеством деталей;
б) вместо того чтобы вводить отдельный элемент для каждой концентрированной нагрузки, элементы надо расположить таким образом, чтобы нести несколько видов нагрузки [6];
в) нагрузки могут быть более эффективно восприниматься элементами, работающими на растяжение или сжатие, чем элементами, работающими на изгиб или кручение;
г) самый короткий путь является самым лёгким как для элемента, несущего нагрузку [7]
Применение описанных выше методик расчёта и методов совершенствования конструкций может существенно помочь проектировщикам на стадии проектирования и как следствие повысить их производительность труда и безопасность конструкций.
Литература:
1. Нежданов К. К., Лаштанкин А. С., Гарькин И.Н Сборные подкрановые балки из прокатных профилей // Строительная механика и расчёт сооружений.: № 3 -2013,с.69–75 Москва ЦНИСК им.Курчеренко
2. Нежданов К. К., Железняков Л. А., Гарькин И. Н. Эффективный способ проката уголкового профиля // Строительная механика и расчёт сооружений № 1 -2014, с.71–75 Москва ЦНИСК им.Курчеренко
3. Арискин М. В., Гуляев Д. В., Агеева И. Ю., Гарькин И.Н Теоретические исследования напряженно-деформированного состояния элементов соединений на вклеенных шайбах [Текст] // Молодой ученый. — 2013. — № 2. — С. 27–31.
4. Данилов А. М., Гарькин И. А., Гарькин И. Н. Управление объектами на подвижном основании: оптимизация конструктивной и структурной схем // Региональная архитектура и строительства. — 2014.– № 3. С. 102–108
5. Гарькин И. А., Гарькин И. Н. Идентификация и аппроксимация колебаний конструктивных элементов [Текст] // Молодой ученый. — 2013. — № 3. — С. 44–48.
6. Фадеева Г. Д. Методы усовершенствования конструкций [Текст] / Г. Д. Фадеева, К. С. Паршина, Е. В. Родина // Молодой ученый. — 2013. — № 6. — С. 158–160.
7. Хейвуд Р. Б. (Heywood R. B.) Проектирование с учётом усталости (Designing against fatigue. london. 1962). Перевод с английского докторов техн. наук В. П. Григорьева и В. А. Марьина, кандидатов техн. наук Б. В. Заславского и Э. Д. Скурлатова, инж. И. Н. Землянских. Под редакцией чл. корр. АН СССР И. Ф. Образцова. Издательство «Машиностроение», Москва, 1969. 504 с.







