Рассматриваются преобразования структурной схемы целостной эргатической системы для управления продольным движением транспортного самолета на стадии когнитивного моделирования.
Ключевые слова: эргатические системы, структуризация, продольное движение, параметрическая идентификация, когнитивное моделирование.
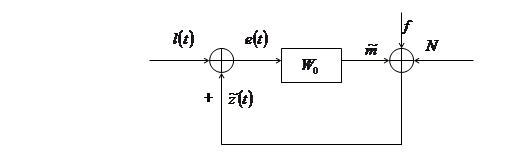
Основная трудность идентификации целостной эргатической системы заключается в переходе от описательных структурных схем к формализуемым. Она связана с организмическим принципом управления в эргатической системе (объект предопределяет поведение оператора; управление организмически оптимально). Так, в соответствии с уравнениями продольного движения [1…3] транспортного самолета структурную схему эргатической системы можно привести к виду, изображенному на рис.1. Ее можно преобразовать к виду, приведенному на рис.2. Здесь достаточно ясными становятся трудности, возникающие при формализации эргатической системы в терминах автоматического регулирования. Они заключаются в составлении уравнения замыкания, а также в определении некоторой эквивалентной передаточной функции 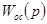 , характеризующей связь мысленного образа
, характеризующей связь мысленного образа 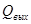 выходной координаты
выходной координаты  .
.
Нетрудно видеть, что предлагаемая на рис.2 структурная схема является лишь детализацией схемы, приведенной на рис.1.
Действительно, в результате структурных преобразований схемы 2 легко получить схему, приведенную на рис.1.
Из сравнения схем следует:
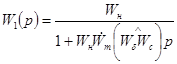 .
.
коэффициенты 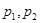 характеризуют
характеризуют 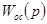 . При необходимости вместо них можно взять более сложные передаточные функции. Проведя приводимые структурные преобразования схемы 2, получим схемы, изображенные на рис.3,4.
. При необходимости вместо них можно взять более сложные передаточные функции. Проведя приводимые структурные преобразования схемы 2, получим схемы, изображенные на рис.3,4.
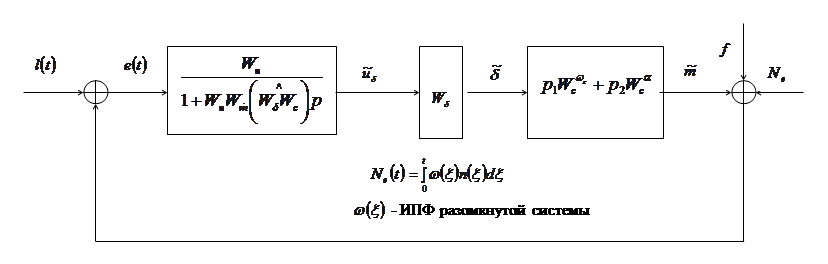
Рис. 1
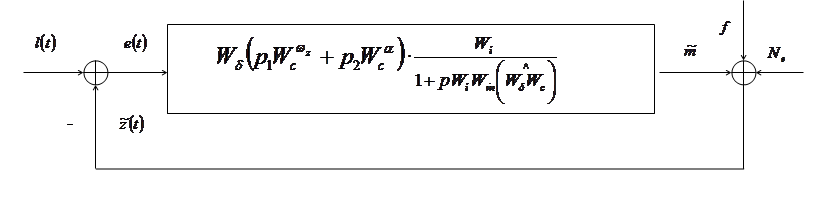
Рис. 2
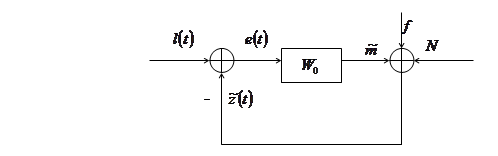
Рис. 3
 ;
; 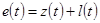 ;
; 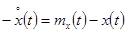
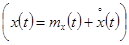
Рис. 4
Сигнал  позволяет определить программное движение и сигнал по стабилизации программного движения. Это позволяет составить уравнение замыкания в терминах отклонения ручки управления, то есть программное движение задавать функцией
позволяет определить программное движение и сигнал по стабилизации программного движения. Это позволяет составить уравнение замыкания в терминах отклонения ручки управления, то есть программное движение задавать функцией  , выходную координату — функцией
, выходную координату — функцией 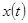 , а ошибку — функцией
, а ошибку — функцией 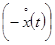 . При этом получим верное равенство
. При этом получим верное равенство
 .
.
Как видим, эргатическая система оказалась формализованной.
Для идентификации передаточной функции 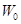 можно воспользоваться соотношением:
можно воспользоваться соотношением:
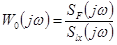 ,
,
где
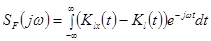 ,
,
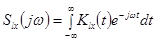 ,
,
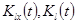 — корреляционные функции.
— корреляционные функции.
Приближенные значения неизвестных параметров объекта и человека-оператора можно определить по полученной передаточной функции 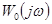 (в соответствии со структурными схемами 3,4).
(в соответствии со структурными схемами 3,4).
Приведенный подход использовался на стадии когнитивного моделирования продольного движения рассматриваемых целостных эргатических систем [4…6].
Литература:
1. Andreev A. N., Danilov A. M., Klyuev B. V., Lapshin E. V., Blinov A. V., Yurkov N. K. Information models for designing conceptual broad-profile flight simulators / Measurement Techniques. August 2000. — Vol.43. Issue 8. — P.667–672.
2. Будылина Е. А., Гарькина И. А., Данилов А. М. Приближенные методы декомпозиции при настройке имитаторов динамических систем / Региональная архитектура и строительство. — 2013. — № 3. — С. 150–156.
3. Гарькина И. А., Данилов А. М., Королев Е. В. Когнитивное моделирование при синтезе композиционных материалов как сложных систем / Известия высших учебных заведений. Строительство. — 2009. — № 3–4. — С. 30–37.
4. Данилов А. М., Гарькина И. А. Теория вероятностей и математическая статистика с инженерными приложениями: учебное пособие. — Пенза: ПГУАС. — 2010. — 228 с.
5. E. Budylina, A. Danilov. Approximation of aerodynamic coefficients in the flight dynamics simulator Contemporary Engineering Sciences, Vol. 8, 2015, no. 10, 415–420 http://dx.doi.org/10.12988/ces.2015.5256
6. Гарькина И. А., Сухов Я. И. Некоторые соображения о корректности и точности линейной аппроксимации уравнений движения эргатической системы / Молодой ученый.- № 3(83). — 2015. — С. 245–247.







