Разработка алгоритма для управляющих действий боковым движением самолета при заходе на взлетно-посадочную полосу



В статье приводятся принципы составления правил логического вывода для нечеткой системы автоматического управления боковым движением самолета при заходе на взлетно-посадочную полосу. Разработан алгоритм (закон) управления (для управляющих действий) боковым движением самолета в бортовых системах автоматического управления с нечеткой логикой. Приведена процедура вычисления алгоритма нечеткого управления.

Выполнена оценка функциональных возможностей системы уравнений в форме Коши, даны также рекомендации по ее применению и сделаны выводы о перспективах использования подобных алгоритмов.

Даются общие рекомендации по методам нечеткого анализа и синтеза систем управления. Выполнены выводы для определения качественных характеристик для переходных процессов систем.

Ключевые слова: нечеткое управление, система автоматического управления, переходный процесс, алгоритм для управляющих действий, нечеткая логика, боковое движение самолета.

Основным параметром, по которому ведется управление боковым траекторным движением, является крен (γ) [1, 2].

Следует учесть, что информация о боковом отклонении (Z — линейное отклонение, ε — угловое отклонение), например, при посадке, получается с помощью существующих систем посадки или визуального наблюдения взлетно-посадочной полосы (ВПП) оператором.

Чтобы амплитуда колебаний траекторного движения ЛА была достаточно небольшой, необходимо обеспечить эффективное демпфирование колебаний, что достигается введением в закон управления сигналов, пропорциональных скорости изменения бокового отклонения.

Боковое движение центра масс ЛА относительно посадочной траектории описывается уравнениями:

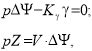(1)

где — крен ЛА; Z — линейное боковое отклонение; V — воздушная скорость полета;  — величина отклонения текущего курса ЛА от заданного значения;- передаточный коэффициент; g-ускорение свободного падения.

Система управления для успешного захода на посадку реализует следующие законы управления:

или (2)

На основе приведенных законов управления могут быть выполнены несколько структурных схем систем управления полетом ЛА.

В зависимости от величины отклонения текущего курса ЛА от его заданного значения  летчик (оператор) меняет крен самолета. Поэтому задачу стабилизации курса ЛА можно представить состоящей из двух более простых задач.

Пусть стоит задача стабилизации центра масс ЛА на заданной траектории в боковом движении. Отметим, что при решении данной задачи оператор должен наблюдать и анализировать показания трех приборов. При этом информация об отклонении  текущего курса от заданного значения используется в качестве информации о скорости (первой производной) отклонения центра масс ЛА от заданной траектории, что справедливо при отсутствии бокового ветра, что выполняется для второго уравнения в соответствии с выражением (2).

С учетом первого уравнения системы (1) устанавливается зависимость между второй производной отклонения и креном ЛА: ppZ ≈ g γ.

При этом первая задача состоит в определении зависимости заданного крена от бокового отклонения Δ Z самолета от заданной траектории и первой производной указанного отклонения. Вторая задача также заключается в обеспечении Δ γ = 0. В данном случае получаем переходные процессы кренового и траекторного движений. Их продолжительность различается в 5–10 раз и более. При таком подходе получить информацию о параметрах движения ЛА оказывается проще. Она носит вычислительный характер. В подобных режимах полета ЛА существенно упрощается работа оператора за счет автоматизирующих решение этой задачи устройств. Управление ЛА с использованием таких систем называют полуавтоматическим управлением, а сами системы — системами полуавтоматического управления.

Целесообразно освободить оператора от управления самолетом вручную, особенно при заходе ЛА на посадку, когда резко возрастает на него нагрузка. Применение в этом случае автопилота позволяет повысить точность стабилизации угловых положений динамического объекта, а значит и точность его стабилизации на посадочной траектории, и быстродействие. Структурная схема системы с автопилотом называется системой траекторного управления. Они отличаются тем, что вместо звена с передаточной функцией оператора включено звено с передаточной функцией автопилота.

Малая высота полета и сложные метеоусловия обусловливают высокие требования к безопасности полета ЛА при заходе на посадку, что связано, в свою очередь, с повышением надежности, точности и быстродействия систем автоматического управления. В настоящее время безопасность полета с помощью автопилота не обеспечена. Отметим две особенности в управлении ЛА.
Во-первых, на основе прибора оператор должен точно обеспечить выполнение условия Δ γ = 0 (γ = γзад.). Во-вторых, время переходных процессов во внутреннем контуре (время установления Δ γ = 0) должно быть в 5–10 раз (и более) меньше времени переходных процессов траекторного движения. Это позволяет при рассмотрении траекторного движения заменять внутренний контур передаточным звеном с единичным усилением, что приводит к упрощению структурной схемы управления боковым движением на заданной траектории.

Следует отметить, что при замене внутреннего контура звеном с единичным усилением динамика движения самолета определяется лишь законом формирования командных сигналов γ.

При использовании законов управления, как в звене «вычислитель СТУ», переходные процессы отличаются от оптимальных процессов.

Обе структурные схемы систем управления отличаются тем, что в первом случае вместо звена с передаточной функцией оператора включено звено с передаточной функцией автопилота.

Поэтому за основу при синтезе нечеткого регулятора принимается поведение оператора в такой ситуации, а сам синтез нечеткого регулятора будет сводиться к синтезу нечеткой системы, в контуре управления которой применяется указанные системы посадки. Суть структурной схемы нечеткой системы управления ЛА состоит в том, что в ее структуру включено звено (нечеткий регулятор) с передаточной функцией Wнр(р). Включение звена с нечеткой передаточной функцией вместо звеньев с или дает ощутимые преимущества в длительности протекании переходных процессов.

Все приведенные правила основаны на небольшом опыте. Так что регулятор либо вырабатывает правила самостоятельно в процессе работы со стационарным объектом, либо (в нашем случае) может улучшать исходный лингвистический алгоритм. Иначе говоря, в алгоритм для вычисления  управляющего действия (в правила нечеткого регулятора) могут быть внесены логические изменения. Предполагается, что они улучшат переходные процессы [3, 4, 5].

Теперь остановимся на определении функций принадлежностей (функций распределения нечеткостей) и выявлении составных (композиционных) правил логического вывода [6, 7].

В общем случае построение систем нечеткого управления до настоящего времени осуществляется эвристическим путем. Это пока неизбежно, поскольку отсутствует теория нечеткого управления и регулирования. Лингвистический подход требует больших затрат времени и квалифицированной работы оператора. Кроме того, порядок систем независимо от порядка процесса остается малым. В литературе не объяснено, что конкретно позволяет делать такие упрощения. При обсуждении моделей управляемого процесса важно правильно выбрать схему управления, что до настоящего времени зависело от опыта и интуиции оператора.

Важным этапом синтеза нечетких систем является составление правила логического вывода. В работах Е. Мамдани используется введенное Л. Заде композиционное правило вывода. Для его составления задается нечеткая импликация R. Для построения другого правила логического вывода можно использовать нечеткие значения истинности. Используется процедура «размытия» бесконечнозначной логики Лукашевича.

Нет серьезных аргументов в пользу данного правила вывода по сравнению с предложенным Л. Заде правилом. В то же время предложенная процедура требует гораздо более сложных вычислений.

Так для бесконечнозначной логики Лукашевича правило логического вывода формируется следующим образом:

если множества и заданы, соответственно, как возможно истинное и выпуклое, и нормальное и выпуклое, то можно написать, что

,

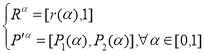где все множества имеют -уровень нечетких множеств,

и тогда

,

где предполагается, что имеются высказывания P и Q, при этом численные значения истинности высказываний соответственно равны p и q .

Для рассматриваемого случая приведем теперь процедуру вычисления нечеткого управления. Пусть алгоритм управления выглядит следующим образом:

Будем искать нечеткое множество , которое индуцируется нечетким множеством D и i-м правилом. На основе формулы для множества находим, что

Далее, определяем с помощью и , и по формуле для указанного выражения отыскиваем :

Общее управляющее воздействие вычисляется в виде

Для рассмотренного алгоритма нет необходимости приводить пример практического применения. Сам алгоритм управления здесь задается эвристически, а не рассчитывается тем или иным способом.

При реализации управления принципиально можно рассматривать процедуру выбора детерминированного элемента базового множества по нечеткому множеству. Эта задача возникает при реализации нечеткого контроллера, который выдает в результате своей работы не конкретное значение управляющего воздействия, а его лингвистическое значение. В большинстве случаев выбирается элемент, имеющий максимальную степень принадлежности к рассчитанному нечеткому множеству. Хотя в другой процедуре выбирается элемент x, соответствующий центру тяжести площади, охваченной графиком функции принадлежности нечеткого множества.

Отметим, что опыт и интуиция операторов приобретаются в процессе труда, то есть нет возможности предсказать появление или не появление действительно единичного события: сколько опыта и интуиции — такова степень достоверности выводов человека, в частности, степень достоверности задания плотностей вероятностей или плотностей нечёткостeй.

Изучив закономерности появления или не появления случайного события, человек получает возможность управлять случайными явлениями. Статистические методы теории вероятностей становятся основным инструментом в современной теории управления. А в настоящее время методы нечеткой теории.

Предположим, что неискушенному в авиации человеку доверили выполнить посадку на самолете. Предварительно требуется научить его управлять самолетом: выполнение разворотов в небе, снижение и набор высоты и т. п. Предложим ему, минуя этап приобретения навыков, посадить самолет на ВПП. Очевидно (исходя из опыта обучения курсантов летных училищ), попытка приведет к аварии. Иначе говоря, качественная оценка движения самолета относительно ВПП не позволяет выполнить единичный эксперимент. Оператор должен приобрести соответствующий опыт в управлении самолетом на посадке, то есть сформировать функцию распределения вероятностей или нечеткостей.

Опорная траектория снижения самолета (глиссада) размыта. Оператор определяет отклонения самолета относительно среднего (номинального) значения опорной траектории. Чем больше величина отклонения, тем меньше «вероятность ошибки» в определении отклонения или выше точность измерения того, что самолет имеет отклонение.

Приведем пример. При бросании монеты (игра в «орлянку») свойство симметрии монеты позволяет сформулировать априорное суждение о равновероятном выпадении «орла» и «решки».

Игра очень проста. Рассмотрим случай игры с двумя монетами. В этом варианте каждый из двух игроков одновременно и независимо бросает монету. Если выпадают одинаковые стороны монет, то выигрывает игрок А, в противном случае — игрок В. Оценим выигрыш игрока А как 1, а его проигрыш — как -1. Матрица игры будет иметь вид:

A\B	/B1	P/B2
(A1)	1	-1	-1
P(A2)	-1	1	-1
	1	1

В этой игре стратегия игрока А является его максиминной, а любая стратегия игрока В — его минимаксной. Седловой точки нет. Оба игрока находятся в равных условиях. Так как выпадение «орла» или «решки» равновероятны, можно утверждать, что средний выигрыш равен нулю, что говорит о справедливости игры. С другой стороны, показано в [8], что, имея аналогичную матрицу игры в «чет и нечет», оптимальным будет такое поведение игроков А и В, при котором они будут использовать смешанную стратегию и чередовать свои чистые стратегии с равными вероятностями (одинаково часто). Иначе говоря, при многократном повторении игры, когда минимакс и максимин не совпадают, теория вероятности позволяет выбрать игрокам наилучшую для себя стратегию не только в случае чистой цены игры, но и тогда, когда значения верхней и нижней цен не совпадают.

Рассмотрим пример игры в «орлянку» при бросании одной монеты.

События А и В несовместимы, так что Р(или А или В) = Р(А)+Р(В). При экспериментов Р(А)=Р(В)=0.5. С уменьшением числа опытов вероятности перераспределяются и для одного эксперимента с той же монетой можно получить две ситуации, которые представим в виде матрицы:

	А	В
х1	0	1	0
х2	1	0	0
	1	1

где для х1, если Р(В)=1, то Р(А)=0, и для х2, если Р(А)=1, то Р(В)=0. И в том и другом случаях Р(или А или В) = 1. Седловой точки нет.

Применяя методику вычисления вероятностей использования чистых стратегий согласно [8], получим Р(А)=Р(В)=0.5. Однако, в работе [9] рассматривается иной исход игры при бросании монеты для двух экспериментов.

Здесь х1 представляет собой характеристическую функцию вида

μ() = 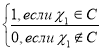или μ(или А или В) =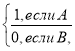

где обычное множество , Х — некоторое множество элементов.

Вероятность . Не нарушая общности рассуждений, примем, что вероятность какого-либо события равна . Однако, в случае субъективного мнения она приобретает вид , то есть становится размытой,

Значит, функция принадлежности имеет вероятностную интерпретацию, и ее можно найти путем экспертного опроса или с помощью статистических данных [10]. Процедуру построения функций принадлежностей удобно построить на основе функций распределения:

— функции распределения вероятностей для нижнего и верхнего порогов (границ) между термами лингвистической переменной.

Развивается направление, связанное с решением задачи анализа и синтеза нечетких регуляторов с помощью лингвистической фазовой плоскости. В настоящее время этот метод изучается более широко, чем метод гармонического баланса, пригодный для анализа нечетких систем малой размерности. Значения, которые принимают лингвистические переменные, предполагаются упорядоченными в естественном смысле. Для этого вводятся понятия типа «отрицательное среднее», которому предшествует «отрицательное малое» и так далее [11].

Рассмотрим протекающие в системе управления процессы.

В качестве размытых переменных состояния выбирается положение ЛА по угловым координатам  (от системы внешних траекторных измерений) и  (собственно угол).

Продольный канал управления не рассматривается.

По величинам переменных пространство состояний разбито на элементы, соответствующие нескольким точкам. Значения переменным присваиваются, используя семь основных размытых подмножеств: ПБ, ПС, ПМ — положительные большое, среднее, малое; НО — ноль; ОМ; ОС; ОБ — отрицательные малое, среднее, большое.

Управляющие действия, как и переменные состояния, могут быть определены субъективно. Однако, учитывая связь между входными и выходными переменными, можно построить управляющие правила в терминах декартова произведения нечетких множеств Аi в Хi, i=1,2,...n, и составлением композиции.

Выход каждого правила является размытым подмножеством, которое определяет степень возможных значений управляющих размытых переменных.

Процедура выбора управляющего действия зависит от степени принадлежности.

Установлено, что при описании системы в пространстве состояний входные векторы в момент измерений могут представлять собой субъективные нечеткие множества. При этом построение системе управления ЛА с помощью множества эвристических понятий, выраженных лингвистически, может происходить с использованием различных с симметричными функциями принадлежностей нечетких моделей. Оператор реализует следующий закон управления:

:

При этом нечеткий контроллер описывается в общем случае уравнениями вида:

, ()

где x — вектор состояния контроллера; е — его вход; u — выход.

Предлагаемая процедура оценивания компоненты истинности вполне применима в проблемах выбора альтернатив (допустимых решений) при управлении самолетами с помощью систем управления.

Рассмотрим возможность использования указанных понятий, играющих основную роль в приложениях математики, для развития теории нечеткого управления, которая строится на нечетких отношениях, и для разработки методики синтеза нечетких информационно-управляющих и информационно-измерительных систем.

Остановимся на определении алгоритма для управляющих действий.

Пусть даны счетные множества А1 и А2 и х — элемент А1, у — элемент А2. Множество упорядоченных пар (х, у) определяет декартово (прямое) произведение А1хА2 (рассматриваются только бинарные нечеткие отношения) [12].

Нечеткое отношение R определяется как нечеткое подмножество, принимающее свои значения в М, то есть , где — плотность нечеткости, значение которой понимается как субъективная мера отношения — конечное упорядоченное множество принадлежностей элементов множества .

Обозначим — элемент множества М. Если и , то определяет нечеткое подмножество, которое можно представить в виде матрицы:

	Y1	Y2	Y3
X1	0.3	0.7	0.9
X2	0.5	0.2	0.3
X3	0.4	0.3	0.6

где матрицы выполняются в виде , i = 1,2,3; j=1,2,3, в частности, и т. д.

Функция принадлежности расплывчатой импликации R (если А, то В) задается в виде:

Тогда для найденного R и заданного А' находим нечеткое множество В' из нечеткого уравнения или

Это соотношение называется составным (композиционным) правилом логического вывода.

Математический смысл в этом случае представляется как...

если «сигнал на входе большой», то «на выходе сигнал средний», или,

если «сигнал на входе средний», то «на выходе сигнал маленький», и т. д.

Функция принадлежности расплывчатой (нечеткой) импликации R, составленной из двух импликаций: если A1, то B1, или, если A2, то B2, имеет вид

При наблюдении за работой оператора установлено [9], что при описании системы в пространстве состояний входные векторы в момент измерений могут представлять собой субъективные нечеткие множества. При этом для построения систем управления с помощью множества эвристических понятий, выраженных лингвистически, можно использовать различные нечеткие модели с симметричными функциями принадлежностей. Рассмотрим одну из таких моделей, принимая во внимание, что оператор реализует следующий закон управления: . Подобные модели можно раскрыть с использованием выше приведенных основных размытых подмножеств в условиях параметров состояния [13].

Приведем в качестве примера простые правила нечеткого логического регулятора типа системы управления боковым движением:

(ОМ, ПМ)  НО, то есть, если «ошибка есть ОМ» и «изменение ошибки есть ПМ», то «изменение в действии есть НО» и т. д.

В качестве входного воздействия следует принять сигналы, которые определяются нечеткими значениями функции ε(t):

от ОМ (-3 В) или ПМ (+3 В) … до ОБ (-9 В) или ПБ (+9 В).

Модель:

	-6	-5	-4	-3	-2	-1	0	1	2	3	4	5	6
ПБ	0	0	0	0	0	0.3	0.4	0.5	0.6	0.7	0.8	0.9	1.0
ПС	0	0	0	0	0	0.3 0.3	0.6 0.5	0.9 0.7	1.0 1.0	0.9 0.7	0.6 0.5	0.30.3	0
ПМ	0	0	0	0	0	0.3 0.3	0.8 0.6	1.0 1.0	0.8 0.6	0.3 0.3	0	0	0
НО	0	0	0	0	0	0.3	1.0	0.3	0	0	0		0
ОМ	0	0	0	0.3	0.8	1.0	0.8	0.3	0	0	0	0	0
ОС	0	0.3	0.6	0.9	1.0	0.9	0.6	0.3	0	0	0	0	0
ОБ	1.0	0.9	0.8	0.7	0.6	0.5	0.4	0.3	0	0	0	0	0

	-7	-6	-5	-4	-3	-2	-1	0	1	2	3	4	5	6	7
ПБ	0	0	0	0	0	0	0.2	0.3	0.4	0.5	0.6	0.7	0.8	0.9	1.0
ПС	0	0	0	0	0	0	0.2	0.5	0.8	1.0	0.8	0.5	0.2	0	0
ПМ	0	0	0	0	0	0	0.2	0.9	1.0	0.9	0.2	0	0	0	0
НО	0	0	0	0	0	0	0.2	1.0	0.2	0	0	0	0	0	0
ОМ	0	0	0	0	0.2	0.9	1.0	0.9	0.2	0	0	0	0	0	0
ОС	0	0	0.2	0.5	0.8	1.0	0.8	0.5	0.2	0	0	0	0	0	0
ОБ	1.0	0.9	0.8	0.7	0.6	0.5	0.4	0.3	0.2	0	0	0	0	0	0

	-7	-6	-5	-4	-3	-2	-1	0	1	2	3	4	5	6	7	8
ПБ	0	0	0	0	0	0	0.1	0.2	0.3	0.4	0.5	0.6	0.7	0.8	0.9	1.0
ПС	0	0	0	0	0	0	0.1	0.4	0.7	0.9	1.0	0.9	0.7	0.4	0.1	0
ПМ	0	0	0	0	0	0	0.1	0.4	0.7	1.0	0.7	0.4	0.1	0	0	0
НО	0	0	0	0	0	0	0.1	1.0	0.1	0	0	0	0	0	0	0
ОМ	0	0	0.1	0.4	0.7	1.0	0.7	0.4	0.1	0	0	0	0	0	0	0
ОС	0.1	0.4	0.7	0.9	1.0	0.9	0.7	0.4	0.1	0	0	0	0	0	0	0
ОБ	0.9	0.8	0.7	0.6	0.5	0.4	0.3	0.2	0.1	0	0	0	0	0	0	0

Исходной процедурой при построении регулятора является задание нечетких множеств в виде функций принадлежностей того или иного вида. Кроме дискретных функций принадлежностей модели можно использовать непрерывные. В общем случае функции принадлежностей могут иметь любой вид кривой с различной степенью принадлежностей.

Для уменьшения статической ошибки нечеткой системы управления можно комбинировать числом элементов базового множества и расстояниями между ними. Поэтому необходимо отметить, что ширина функций принадлежностей для различных параметров выбирается отдельно для каждого параметра (смотри модель).

Это делается, исходя из работ [14, 15, 16], на основании рассмотренной выше модели с дискретным представлением функций принадлежностей переменных состояния. Алгоритм для управляющих действий в структуре системы управления креном самолета при боковом его движении [17] реализуется следующим образом (см. модель выше по тексту) [18, 19], тогда полные правила можно отобразить в виде следующей таблицы:

Если  = ОБ и = не (ОБ или ОС), то  = ПБ; еще:	Если  = ОБ или ОС и = ОМ, то  = ПС; еще:	Если  = ОМ и = ПМ или –НО, то  = ПС; еще:
Если  = НО и = ПБ или ПС, то  = ПС или ОС; еще:	Если  = НО и = ОБ или ОС, то  = ОС или ПС; еще:	Если  = НО и = –НО, то  = –НО; еще:
Если  = ПМ и = ПМ или –НО, то  = ОС; еще:	Если  = ПБ или ПС и = ОМ, то  = ОС; еще:	Если  = ПБ и = не (ОБ или ОС), то  = ОБ; еще:
Если  = –НО и = ПМ, то  = ПМ; еще:	Если  = –НО и = ОМ, то  = ПМ; еще:	Если  = +НО и = ОМ, то  = ПМ или ОМ; еще:
Если  = +НО и = ПМ, то  = ОМ.

При синтезе нечеткой системы управления ЛА наиболее сложными этапами оказываются [20]:

‒ формирование управляющих правил;

‒ отыскание отображений по эвристическим заданным правилам;

‒ обеспечение расчетов нечеткими моделями объекта.

В пространстве состояний нечеткий регулятор можно описать с помощью уравнений в форме Коши (). Исследуя полученную систему уравнений, можно проводить анализ и синтез нечеткого регулятора.

Выводы.

1. Применение в системах управления методов теории нечеткого управления позволяет повысить качество переходных процессов, в частности, быстродействие в 1,5–2 раза, так как оптимальное управление ищется среди приближенных, а не точных стратегий.
2. Низкая алгоритмическая сложность нечеткого математического аппарата позволяет использовать маломощные цифровые вычислительные машины (ЦВМ).
3. Известные системы управления процессом посадки ЛА при внедрении предлагаемых методов и средств не требуют каких-либо серьезных доработок (изменяется только нечеткий алгоритм управления, т. е. его реализация в бортовых ЦВМ).
4. Системы автоматического нечеткого управления обладают высокой технической надежностью.
5. Системы автоматического управления с нечеткой логикой обладают высокой устойчивостью по отношению к внутренним и внешним возмущающим воздействиям.
6. Логико-лингвистический (нечеткий) подход к выбору управляющих стратегий может быть принят за основу при синтезе нечетких систем автоматического управления летательными аппаратами любого назначения.

Литература:

1. Управление воздухоплавательными комплексами: теория и технологии проектирования. Пшихопов В. Х., Медведев М. Ю. и др. — М.: Физматлит, 2010, с. 394.
2. Юревич Е. И. Теория автоматического управления — Санкт-Петербург: «БХВ — Петербург», 2016, с. 560.
3. Aracil J., Gordillo F. Stability issues in fuzzy control. Physica — Verlag, Heidelberg — New York, 2000, pp. 251–256.
4. Piegat A., Plucinski M. Firm evaluation with 2-dimensional projection method. Proceedings of the Fifth International Conference “Neural Networks and Soft Computing”. Zakopane, Poland, 2000, pp. 361–367.
5. Liao S. Y., Wang H. Q., Liu W. Y. Functional dependences with null values, fuzzy values, and crisp values. IEEE Transactions on Fuzzy Systems, vol. 7, № 1, 2000, pp. 97–103.
6. Pfeiffer B. M. Workshop «Fuzzy Control». Automatisierungstechnik, vol. 44, № 3, 1996, pp. 141–142.
7. Rovatti R., Guerieri R. Fuzzy sets of rules for system identification. Transactions on Fuzzy Systems, vol. 4, № 2, 1996, pp. 89–101.
8. Вентцель Е. С. Элементы теории игр. — М.: Физматгиз, 1959, с. 26.
9. Левин Р., Дранг Д., Эделсон Б. Практическое введение в технологию искусственного интеллекта и экспертных систем с иллюстрациями на Бейсике. — М.: Финансы и статистика, 1990, с. 100–103.
10. Борисов А. Н. и др. Обработка нечеткой информации в системах принятия решений. — М.: Радио и связь, 1989, с. 61–64.
11. Давыдов Ю. Т., Репин А. И. Основы оптимизации и комплексирования бортовых информационных систем. — М.: МАИ, 1996, с. 170.
12. Орловский С. А. Проблемы принятия решений при нечеткой исходной информации. — М.: Наука, 1981, с. 36–44.
13. Яшин М. М., Репин А. И. Исследование способа управления при неполной информации. — Материалы научно-технической конференции «Новые информационные технологии», — М.: МГАПИ, 1998, с. 59–65.
14. Нечеткие множества и теория возможностей. Последние достижения. Под ред. Р. Ягера. — М.: Радио и связь, 1986, с. 64–70.
15. Нечеткие множества в моделях управления и искусственного интеллекта. Под ред. Д. А. Поспелова. — М.: 1986, с. 23–29.
16. Вопенка П. Математика в альтернативной теории множеств. — Математика. Новое в зарубежной науке. — М.: МИР, 1983, с. 29–35.
17. Репин А. И., Снедков А. Б., Кашкина Т. И. Анализ переходных процессов в нечеткой системе управления боковым движением самолета. Постановка задачи. — «ВЕСТНИК Московского государственного университета приборостроения и информатики», 2014, № 50, с. 40–46.
18. Репин А. И., Меркишин Г. В., Лосев В. Ю. Переходные процессы в нечеткой системе управления боковым движением самолета. — «ВЕСТНИК Московского авиационного института», 2010, № 4, с.159–163.
19. Репин А. И., Кашкина Т. И. Особенности применения минимаксных операций для управления боковым движением самолета. — «Вестник Московского авиационного института», 2017, № 1, том 25, с. 68–81.
20. Пегат А. Нечеткое моделирование и управление. — М.: Бином. Лаборатория знаний, 2012 (Адаптивные и интеллектуальные системы), 800 с.