Рассмотрим безграничную в плане пластинку толщиной 2h, находящейся под поверхностью полубесконечной среды на глубине (h0- h1). Плоскость (ХҮ) поместим в средней плоскости пластинки z=0. Ось OZ направим в сторону внешней поверхности верхнего слоя.
Для общности материалы верхнего слоя и основания будем считать различными. Обозначим параметры пластинки индексом «1», верхнего слоя индексом «2», основания индексом «3». 1[34]
Рассматривая задачу в трехмерной линейной постановке, уравнения движения слоя пластинки и основания с учетом вязкости и температуры в потенциалах Ф и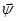 
продольных и поперечных волн запишем в виде:
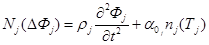
(1.1.)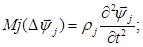
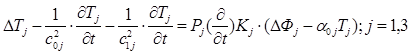
где операторы N j; Kj равны
N j=Lj+2Mj; Kj= Lj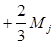
а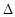 
-трехмерный оператор Лапласа
= 
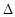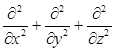
Lj ,Mj - вязкоупругие операторы
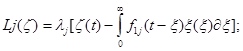(1.2.)
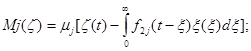
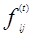- ядра операторов (l=1,2), 
, 
, 
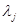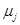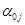- постоянные материалов.
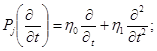(1.3.)
Где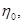 
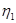- коэффициенты связности.
Предпологая материалы слоя, пластинки и основания вязкоупругими и изотропными, зависимости напряжение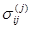 
от деформации 
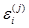с учетом влияния температуры Тj запишем в виде операторных соотношений больцмановского типа
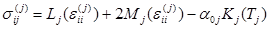(1.4.)
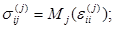
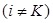
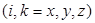
Будем считать, что колебания пластинки под поверхностью могут быть вызваны как внешними усилиями на внешней поверхности z=h0, так и возмущениями распространияющимися со стороны основания. Кроме того, будем считать, что по границам контакта z= h1 и z= h1 пластинки с верхним слоем и основанием, эти контакты идеальные, т.е. отсутствует трение. Тогда будем иметь следующие граничные условия: на внешней стороне (z=h0)
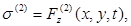
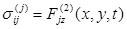
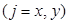(1.5.)
И одним из трех условий для Т2
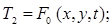
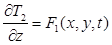(1.6.)
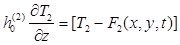
На границе контакта верхний слой – пластинка z= h1
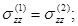
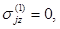
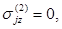w(1)= w(2) (j=х, у) (1.7.)
и для температуры Тj (j=1.2)
T1=T2 ;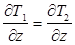 
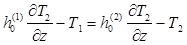
На границе пластинка – основание z=-h1
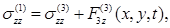
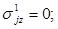(1.8.)
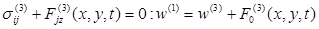(j=х, у)
и для температуры Тj (j=1.3)
T1=T3 ;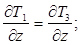 
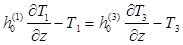
где функции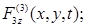 
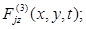
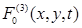описывают напряжения и смещения в падающей волне снизу, т.е. со стороны основания, что может быть вызвано, в частности, землетрясением или взрывом, 
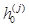- коэффициенты теплопроводности.
Кроме того, должны выполняться условия затухания на бесконечности, т.е. при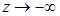 
Ф(3) = 0,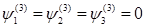 
(1.8.)
Начальные условия нулевые
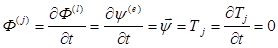
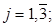при t=0 (1.9.)
Таким образом, краевая задача колебания пластинки, находящейся под поверхностью с учетом влияния температуры, сводится к решению интегродифференциальных уравнений (1.1.) при граничных и начальных условиях (1.5-1.9).
В дальнейшем рассмотрим случай колебания пластинки находящейся под поверхностью без учета температуры и колебания плоского элемента лежащего на деформируемом основании с учетом температуры.
Литература:
1. Филиппов И.Г., Чебан В.Г. Математическая теория колебаний упругих и вязкоупругих пластин и стержней. – Кишинев: Штиинца, 1988. - 190 с.
2. Филиппов И.Г., Халикулов Ш. К Теории колебаний изотропной вязкоупругой пластинки с учетом температуры. – М, 1986. Деп. Во ВНИИКСе №6194.
3. Джанмулдаев Б.Д. Математические методы при исследовании колебаний плоских элементов конструкций, взаимодействующих с деформируемой средой. – Кызылорда, 2002.
4. Егорычев О.А. Филиппов И.Г. Математические методы при исследовании колебаний плоских элементов строительных конструкций. – Труды Российско-Польского семинара «Теоретические основы строительства». - Варшава, 1995. - С. 49-50.
