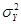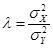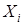Поверка средств измерений (СИ) предполагает построение их градуировочных характеристик (ГХ), под которыми понимается функциональная зависимость 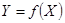 (
(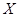 и
и 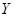 — соответственно входная и выходная величины), построенная на основе результатов измерений (
— соответственно входная и выходная величины), построенная на основе результатов измерений (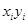 ),
), 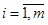 ; может представляться таблицей, графиком, формулой. Погрешность градуировочной характеристики в точке
; может представляться таблицей, графиком, формулой. Погрешность градуировочной характеристики в точке 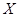 будет равна
будет равна
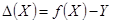 ,
,
где 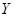 — истинное значение выходной величины
— истинное значение выходной величины 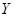 в точке
в точке 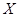 . В числе наиболее распространенных функциональных зависимостей:
. В числе наиболее распространенных функциональных зависимостей:
- линейные 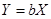 ;
; 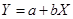 ;
; 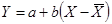 ;
;
- степенные, показательные и дробно-линейные функции 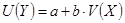 ; приводятся к линейным путем замены переменных
; приводятся к линейным путем замены переменных 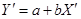 ,
, 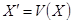 ,
, 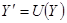 ;
;
- нелинейные 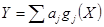 ,
, 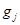 — известные функции;
— известные функции; 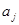 — определяемые коэффициенты (
— определяемые коэффициенты (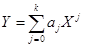 ,
, 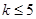 ; разложения по ортогональным полиномам
; разложения по ортогональным полиномам 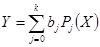 ,
, 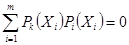 при
при 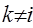 ;
; 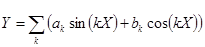 .
.
При их получении используются априорные данные:
- о значениях входных величин 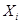 ;
;
- о функциональном виде ГХ;
- о виде распределения случайных погрешностей измерений величин 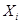 и
и 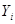 ;
;
- о характеристиках погрешностей измерений 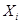 и
и 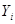 .
.
При линейном или полиномиальном виде и точно известных значениях 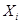 при их построении используются: при гауссовских распределениях погрешностей измерений
при их построении используются: при гауссовских распределениях погрешностей измерений 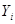 — метод наименьших квадратов (МНК); при распределениях погрешностей измерений
— метод наименьших квадратов (МНК); при распределениях погрешностей измерений 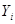 , отличных от гауссовских — робастные методы (усеченный МНК или М-оценки Хубера).
, отличных от гауссовских — робастные методы (усеченный МНК или М-оценки Хубера).
При существенных погрешностях измерений 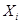 в предположении линейной зависимости используются: в случае гауссовского распределения погрешностей (
в предположении линейной зависимости используются: в случае гауссовского распределения погрешностей (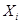 ,
, 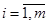 выбираются исследователем и выполняется
выбираются исследователем и выполняется 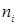 наблюдений при каждом
наблюдений при каждом 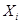 ) — МНК; для случаев, когда
) — МНК; для случаев, когда 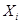 определяются условиями эксперимента и не могут быть выбраны исследователем, — один из конфлюэнтных методов (табл.1).
определяются условиями эксперимента и не могут быть выбраны исследователем, — один из конфлюэнтных методов (табл.1).
Таблица 1
Методы построения ГХ
|
№ |
Априорная информация |
Методы построения ГХ |
|||
|
Вид ГХ |
Распределения погрешностей |
Дисперсии погрешностей |
Значения аргументов |
||
|
1 |
Линейный |
Гауссовские |
Постоянны |
Точные |
Метод наименьших квадратов (МНК) |
|
2 |
Известны веса |
МНК с весами |
|||
|
3 |
Постоянны |
Планируемые |
МНК с учетом приведенных погрешностей |
||
|
4 |
Близки к гауссовским |
Точные |
Усеченный МНК |
||
|
5 |
Известны веса |
Усеченный МНК с весами |
|||
|
6 |
М-оценки Хубера |
||||
|
7 |
Линейный |
Гауссовские |
Известны |
Содержат погрешности |
Модифицированный МНК |
|
8 |
Известно |
Метод ортогональной регрессии |
|||
|
9 |
Произвольны |
Постоянны |
Известен порядок |
Дробно-линейные оценки |
|
|
10 |
Равномерны по диапазону |
Оценка Хаузнера-Бреннана |
|||
|
11 |
Разбиты на 2 или 3 группы |
Оценки Вальда или Бартлетта |
|||
|
12 |
Приводим к линейному |
Гауссовские |
Постоянны |
Точные |
МНК с весами |
|
13 |
Известны веса |
МНК с модифицированными весами |
|||
|
14 |
Близки к гауссовским |
Известны веса |
Точные |
М-оценки Хубера с весами |
|
|
15 |
Гауссовские |
Постоянны |
Планируемы |
МНК с учетом погрешностей |
|
|
16 |
Известны |
Содержат погрешности |
Модифицированный МНК |
||
|
17 |
Полином |
Постоянны |
Точные |
МНК |
|
|
18 |
Известны веса |
МНК с весами |
|||
|
19 |
Близки к гауссовским |
Постоянны |
Усеченный МНК |
||
|
20 |
М-оценки Хубера |
||||
При заданных границах погрешностей 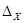 и
и 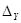 оцениваются границы суммарной погрешности в точке
оцениваются границы суммарной погрешности в точке 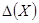 или общие границы по диапазону
или общие границы по диапазону 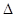 ; при известных СКО
; при известных СКО 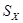 и
и 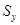 случайных погрешностей и границах
случайных погрешностей и границах 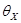 и
и 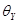 систематических погрешностей — характеристики
систематических погрешностей — характеристики 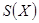 ,
,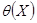 составляющих погрешности.
составляющих погрешности.
Границы погрешностей ГХ при заданных границах погрешностей измерений величин 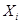 и
и 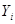 оцениваются в виде:
оцениваются в виде:
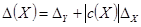 ,
, 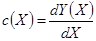 — в точке
— в точке 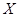 ;
;
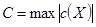 — по диапазону
— по диапазону 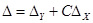 .
.
При отсутствии априорных данных о коэффициентах 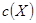 принимается:
принимается:
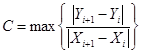 .
.
Если заданы характеристики составляющих погрешностей входных и выходных величин, то характеристики погрешностей в точке 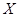 оценивают по формулам:
оценивают по формулам:
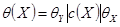 ,
, 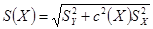 .
.
Доверительные границы случайной погрешности в точке 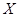 :
:
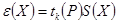 ,
,
где 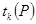 — коэффициент Стьюдента при вероятности
— коэффициент Стьюдента при вероятности 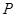 с числом степеней свободы
с числом степеней свободы 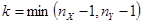 ;
; 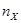 и
и 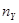 — объемы выборок при оценивании
— объемы выборок при оценивании 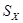 и
и 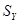 . Если ГХ есть функция заданного вида
. Если ГХ есть функция заданного вида 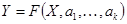 , то оценивание погрешностей производится по линеаризованному разложению. При известных погрешностях исходных данных
, то оценивание погрешностей производится по линеаризованному разложению. При известных погрешностях исходных данных 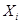 и
и 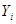 или, если их систематические составляющие изменяются нерегулярным образом в заданных границах, можно построить приближенные доверительные границы погрешности в точке
или, если их систематические составляющие изменяются нерегулярным образом в заданных границах, можно построить приближенные доверительные границы погрешности в точке 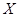 или ее систематической составляющей. При точно известных значениях входных величин
или ее систематической составляющей. При точно известных значениях входных величин 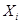 и гауссовских распределениях погрешностей измерений выходных величин параметры линейной ГХ
и гауссовских распределениях погрешностей измерений выходных величин параметры линейной ГХ 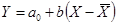 определяются по методу наименьших квадратов (
определяются по методу наименьших квадратов (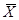 — среднее (взвешенное) значений
— среднее (взвешенное) значений 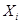 ).
).
При равноточных многократных измерениях выходных величин 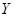 оценки коэффициентов ГХ определяются по формулам:
оценки коэффициентов ГХ определяются по формулам:
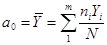 ;
; 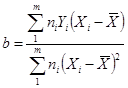 ;
;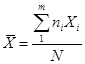 ;
;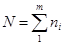 ;
;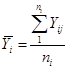 .
.
Границы погрешностей определения коэффициентов 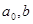 :
:
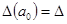 ,
, 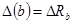 ,
, 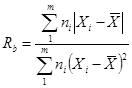 ;
;
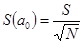 ,
, 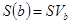 ,
, 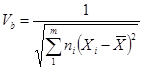 ;
;
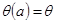 ,
, 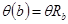 ;
;
граница погрешности ГХ в точке 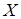 определяется в виде:
определяется в виде:
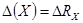 ,
, 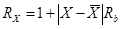 ;
;
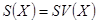 ,
, 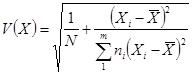 ;
;
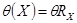 .
.
Характеристики погрешностей для различных видов измерений приводятся в [1].
Если погрешности измерений 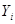 изменяются нерегулярным образом в заданных границах
изменяются нерегулярным образом в заданных границах 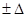 , то приближенные доверительные границы погрешностей коэффициентов и расчетных значений ГХ определяются по формулам:
, то приближенные доверительные границы погрешностей коэффициентов и расчетных значений ГХ определяются по формулам:
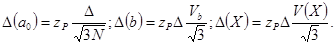
Если систематические погрешности измерений 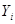 изменяются нерегулярным образом в заданных границах
изменяются нерегулярным образом в заданных границах 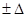 , то приближенные доверительные границы систематических погрешностей коэффициентов и расчетных значений ГХ определяются по формулам:
, то приближенные доверительные границы систематических погрешностей коэффициентов и расчетных значений ГХ определяются по формулам:
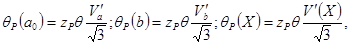
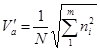 ;
;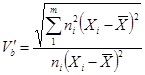 ;
;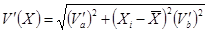 .
.
Доверительные границы случайных погрешностей коэффициентов и расчетных значений ГХ определяются по формулам:
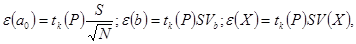
где 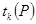 — коэффициент Стьюдента, с числом степеней свободы
— коэффициент Стьюдента, с числом степеней свободы 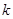 , соответствующим используемой оценке СКО
, соответствующим используемой оценке СКО 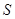 .
.
Указанные методы построения градуировочных характеристик использовались при построении по экспериментальным данным ряда аналитических зависимостей для описания кинетических процессов формирования физико-механических характеристик композитов [2…7].
Литература:
1. Планирование эксперимента. Обработка опытных данных: монография/ И. А. Гарькина [и др.]; под ред. проф. А. М. Данилова. — М.: Палеотип. — 2005. — 272с.
2. Данилов А. М., Гарькина И. А. Интерполяция, аппроксимация, оптимизация: анализ и синтез сложных систем: монография. — Пенза: ПГУАС. –2014. — 168 с.
3. Данилов А. М., Гарькина И. А. Теория вероятностей и математическая статистика с инженерными приложениями. — Пенза: ПГУАС. — 2010. — 228 с.
4. Гарькина И. А. Формализация оценки структуры и свойств композиционных материалов специального назначения / Строительные материалы. — 2007. — № 1. — С. 70–72.
5. Будылина Е. А., Гарькина И. А., Сухов Я. И. Математическое моделирование кинетических процессов в дисперсных системах / Молодой ученый. — 2013. — № 12 (59). — С. 104–107.
6. Гарькина И. А., Данилов А. М., Смирнов В. А.Флокуляция в дисперсных системах / Системы управления и информационные технологии. — 2008. — № 2.3 (32). — С. 344–346
7. Гарькина И. А., Данилов А. М., Домке Э. Р.Промышленные приложения системных методологий, теорий идентификации и управления / Вестник Московского автомобильно-дорожного государственного технического университета (МАДИ). — 2009. — № 2. — С. 77–81.







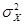 или
или