Рассмотрена методика сокращения вычислительных затрат при выполнении алгоритма UCA‑Root‑Rare, за счёт сокращения степени полинома. Приведены формулы расчета максимальной степени усечения. Приведены результаты численного моделирования.
Введение. Оценивание местоположения множества источников радиоизлучения (ИРИ) узкополосных сигналов является классической задачей в рамках обработки информации, полученной АР. При оценивании координат ИРИ могут использоваться корреляционные алгоритмы [1]. Существующие корреляционные алгоритмы принято делить на два класса: требующие выполнения двухмерного поиска и свободные от него. Применение свободного от двухмерного поиска алгоритма Root‑MUSIC к однородной кольцевой антенной решётке (ОКАР) не возможно напрямую. Однако модификация алгоритма Root‑MUSIC применительно к ОКАР существует и в зарубежной литературе обозначается как UCA‑Root‑Rare [2]. Выполнение данного алгоритма связано с нахождением корней полинома [3]. Проведённые исследования этого полинома показывают, что он обладает свойствами, которые позволяют сократить его степень без потери значимых корней, соответствующих координатам ИРИ.
Цель статьи — разработать метод, позволяющий уменьшить вычислительные затраты, используя свойства полинома, получаемого в результате выполнения алгоритма UCA‑Root‑Rare. Получить ограничения применения предлагаемого метода. Привести результаты численного моделирования.
1. Алгоритм UCA‑Root‑Rare
Вычисление азимута ИРИ при помощи алгоритма UCA‑Root‑Rare предполагает нахождение корней следующего полиномиального уравнения:
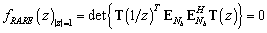(1)
Описание переменных уравнения (1), а также последовательность его получения приведены в [2].
2. Предлагаемое решение
Получаемый в результате нахождения определителя (1) полином, обладает следующими свойствами:
1) общее число корней и степень полинома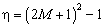 
;
2) если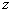 
является корнем уравнения (1), то 
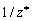также является корнем уравнения (1), где 
— знак комплексного сопряжения. Это означает, что любому корню, находящемуся внутри единичной окружности соответствует корень, расположенный с внешней стороны окружности;
3) если 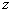является корнем уравнения (1), то 
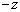также является корнем уравнения (1). Это означает, что любому корню уравнения (1) соответствует корень, находящийся симметрично относительно начала координат. Иными словами, корню 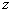соответствует корень 
;
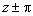4) коэффициенты полинома являются комплексными числами, за исключением коэффициента при степени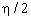 
;
5) коэффициенты являются симметричными комплексно‑сопряжёнными числами, относительно коэффициента при степени .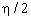
На рисунке 1 в логарифмическом масштабе отображены модули коэффициентов полинома, полученные при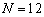 
, 
, 
, 
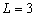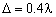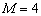. На рисунке 1 символом «•» обозначен модуль коэффициента.
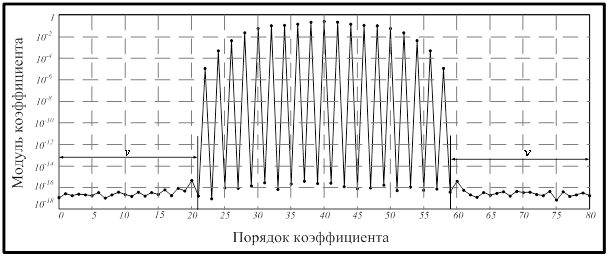
Рис. 1. Модули коэффициентов полинома, полученного при , , ,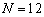
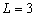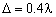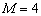
Как следует из рисунка 1, имеется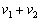 
коэффициентов, расположенных подряд, модуль которых имеет значение много меньшее чем, остальных 
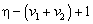коэффициентов. Здесь 
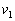— число коэффициентов, стоящих при малых степенях, 
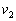— число коэффициентов, стоящих при старших степенях полинома. Следовательно, можно сделать предположение, что сокращение степени полинома, путем удаления 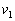слагаемых «спереди» и 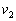слагаемых «сзади» полинома не приведет к потере значимых корней, соответствующих угловым положениям ИРИ. В общем случае, согласно свойствам 4 и 5, следует сделать вывод, что 
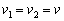. Тогда число удаляемых коэффициентов составит 
.
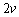Значение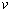 
может быть рассчитано по следующей формуле, которая получена эмпирическим путем, в результате численного анализа:
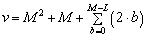(2)
Из приведённого выражения видно, что число усекаемых коэффициентов не зависит от параметров сигналов, а зависит только от параметров конфигурации ОКАР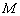 
и числа ИРИ 
.
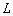Используя формулу (2) можно составить таблицу 1 а), которая покажет максимально допустимое число усекаемых коэффициентов 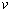при младших или старших степенях полинома. Соответственно общее число усекаемых коэффициентов составит 
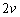. В таблице 1 б) приведено оставшиеся число коэффициентов после усечения полинома справа и слева.
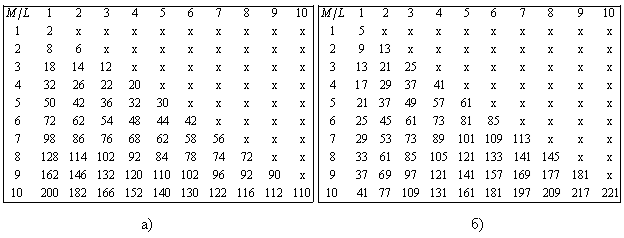
Рис. 2. а) число усекаемых коэффициентов 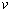; б) оставшиеся число коэффициентов
Символом «x» в таблице 1 отображены значения 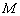и , при которых алгоритм UCA‑Root‑Rare оказывается не работоспособным. Очевидно, что эти значения удовлетворяют неравенству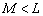 
. Это отнюдь не означает, что полином не имеет корней. Просто корни не соответствуют координатам азимута ИРИ. Корней в этих случаях также 
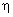. Таблица 1 а) отображена в виде графических зависимостей на рисунке 3.
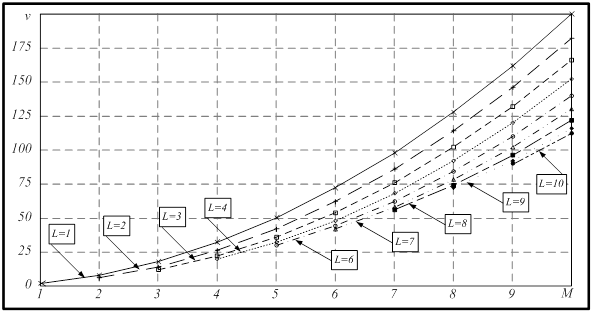
Рис. 3. Число усекаемых коэффициентов 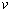при различных значениях 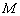и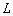
Приведённые зависимости на рисунке 3 показывают, что число усекаемых корней уменьшается при увеличении числа ИРИ 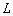при фиксированном значении 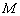. Следует обратить внимание на тот факт, что после усечения полинома справа и слева, оставшиеся коэффициенты нумеруются с 0.
3. Моделирование
Моделирование предлагаемого решения уменьшения вычислительных затрат, проводится для ОКАР с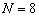 
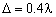, . Число ИРИ 
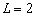с координатами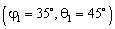 
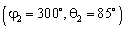, отношение сигнал‑шум 
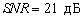. На рисунке 4 приведены результаты вычисления корней полинома, полученного в результате нахождения координат алгоритмом UCA‑Root‑Rare. На рисунке 4 символом «▲» отображены заданные координаты азимута ИРИ, символом «○» корни не модифицированного полинома, символом «•» корни модифицированного полинома.
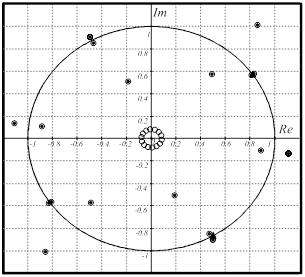
Рис. 4. Результат применения предлагаемого метода
Результаты проведённого моделирования показывают, что корни модифицированного полинома равны корням не модифицированного полинома, за исключением корней, расположенных кольцом вблизи центра окружности и им симметричных корней, удовлетворяющих свойству 2. При этом сохраняются все значимые корни, соответствующие заданным азимутальным положениям ИРИ. Следовательно, предлагаемый метод уменьшения вычислительных затрат может быть использован для алгоритма UCA‑Root‑Rare.
Заключение. Предложен метод уменьшения вычислительных затрат при нахождении корней полинома, получаемого процессе применения алгоритма оценивания местоположения ИРИ UCA‑Root‑Rare. Приведена формула расчёта числа усекаемых корней. Показано, что применяя данный метод, удаётся уменьшить степень полинома без потери значимых корней, соответствующих угловым положениям ИРИ. Уменьшение степени полинома приведет к уменьшению вычислительных затрат, связанных поиском его корней.
Литература:
1. Коробков М. А. Корреляционные методы пеленгования источников излучения // Молодой ученый. — 2014. — № 13. — с. 55–58.
2. Коробков М. А. Алгоритм UCA–Root–Rare для задач пеленгования источников радиоизлучения однородной кольцевой антенной решёткой // Молодой ученый. — 2014. — № 13. — с. 47–54.
3. Коробков М. А. Методы нахождения корней полинома в алгоритме пеленгования UCA‑Root‑Rare в пакете Mathcad // Молодой ученый. — 2014. — № 14. — с. 54–56.
