Рассматривается оценка психофизиологической напряженности оператора в семибалльной оценочной шкале при управлении транспортным средством в зависимости от жесткости рулевого колеса с использованием ортогональных полиномов Чебышева.
Приведем предварительные сведения о разложении функций по ортонормированной системе функций, в частности, полиномов.
Пусть на множестве точек ![]() (
(![]() ) задана функция
) задана функция ![]() и определена система функций
и определена система функций ![]() .
.
Скалярным произведением функций ![]() и
и ![]() на множестве точек
на множестве точек ![]() (
(![]() ) называется
) называется
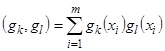 .
.
Число 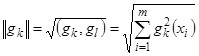 является нормой функции
является нормой функции ![]() на множестве точек
на множестве точек![]() (
(![]() ).
).
Функции ![]() и
и ![]() называются ортогональными на множестве точек, если для скалярного произведения на этом множестве справедливо:
называются ортогональными на множестве точек, если для скалярного произведения на этом множестве справедливо:
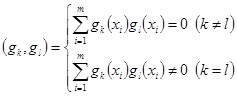 . (1)
. (1)
Система функций ![]() называется ортогональной на множестве точек
называется ортогональной на множестве точек ![]() (
(![]() ), если все функции этой системы попарно ортогональны на этом множестве.
), если все функции этой системы попарно ортогональны на этом множестве.
Коэффициенты ![]() обобщенного многочлена
обобщенного многочлена
![]()
называются коэффициентами Фурье функции ![]() относительно ортогональной системы функций, если они определяются по формулам
относительно ортогональной системы функций, если они определяются по формулам
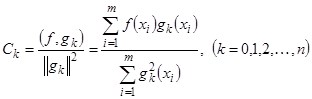 . (2)
. (2)
Для функции ![]() , определенной на множестве точек
, определенной на множестве точек ![]() (
(![]() ), обобщенный многочлен n-й степени
), обобщенный многочлен n-й степени ![]() с коэффициентами Фурье относительно ортогональной на множестве точек системы функций является многочленом наилучшего среднеквадратичного приближения этой функции, причем квадрат наименьшего отклонения равен
с коэффициентами Фурье относительно ортогональной на множестве точек системы функций является многочленом наилучшего среднеквадратичного приближения этой функции, причем квадрат наименьшего отклонения равен
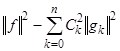 , (3)
, (3)
где Ck — коэффициенты Фурье, определяемые по формулам (2).
Оценка погрешности приближения определяется величиной ![]() .
.
Многочленами Чебышева на множестве точек ![]() (
(![]() ) называются алгебраические многочлены, ортогональные на этом множестве, с нормой
) называются алгебраические многочлены, ортогональные на этом множестве, с нормой ![]() , отличной от нуля, и определяемые следующими рекуррентными формулами:
, отличной от нуля, и определяемые следующими рекуррентными формулами:
![]() (4)
(4)
где
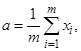
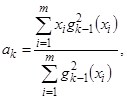
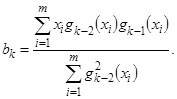
Соотношения для коэффициентов ![]() получаются из условия ортогональности (1).
получаются из условия ортогональности (1).
Можно показать, что многочлен ![]() степени m на множестве точек
степени m на множестве точек ![]() (
(![]() ), полученный по рекуррентным формулам (4), на этом множестве точек имеет норму, равную нулю, и уже не является многочленом Чебышева.
), полученный по рекуррентным формулам (4), на этом множестве точек имеет норму, равную нулю, и уже не является многочленом Чебышева.
Рассмотрим одно приложение к решению актуальной задачи определения аналитической зависимости психофизиологической напряженности оператора ![]() (в семибалльной шкале [1]) от жесткости
(в семибалльной шкале [1]) от жесткости ![]() [Н-м/градус] рулевого управления (приложение момента к рулевому колесу). Экспериментальные данные приведены в таблице:
[Н-м/градус] рулевого управления (приложение момента к рулевому колесу). Экспериментальные данные приведены в таблице:
|
Жесткость |
0 |
1 |
3 |
4 |
|
Класс |
4 |
0 |
1 |
2 |
Составим ортогональные многочлены Чебышева ![]() на множестве точек {0, 1, 3, 4}. Имеем:
на множестве точек {0, 1, 3, 4}. Имеем:
![]()
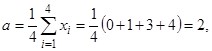
![]()
![]() ;
;
![]()
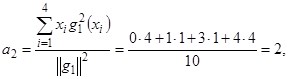
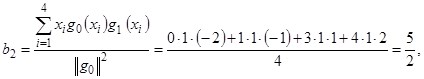
![]()
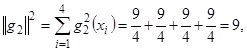
![]() ,
,
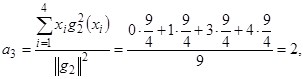
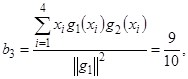
![]() ,
,
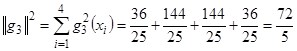 .
.
Значения многочленов ![]() на множестве точек {0, 1, 3, 4} представлены в таблице.
на множестве точек {0, 1, 3, 4} представлены в таблице.
|
|
|
|
|
|
|
|
1 |
0 |
1 |
–2 |
1,5 |
–1,2 |
|
2 |
1 |
1 |
–1 |
–1,5 |
2,4 |
|
3 |
3 |
1 |
1 |
–1,5 |
–2,4 |
|
4 |
4 |
1 |
2 |
1,5 |
1,2 |
Многочлены наилучшего приближения имеют вид:
![]()
![]()
![]()
![]()
Здесь коэффициенты Фурье определены по формулам (2):
![]()
Квадрат наименьшего среднеквадратичного отклонения определяется для приближения многочленом ![]()
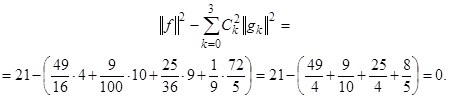
Значения алгебраических многочленов наилучшего среднеквадратичного приближения в точках ![]() представлены в таблице:
представлены в таблице:
|
|
|
|
|
|
|
|
1 |
0 |
1,75 |
2,35 |
3,6 |
4,00 |
|
2 |
1 |
1,75 |
2,05 |
0,8 |
0,00 |
|
3 |
3 |
1,75 |
1,45 |
0,2 |
1,00 |
|
4 |
4 |
1,75 |
1,15 |
2,4 |
2,00 |
Графики функций ![]() изображены на рис. 1 (очевидна целесообразность увеличения числа экспериментальных точек).
изображены на рис. 1 (очевидна целесообразность увеличения числа экспериментальных точек).
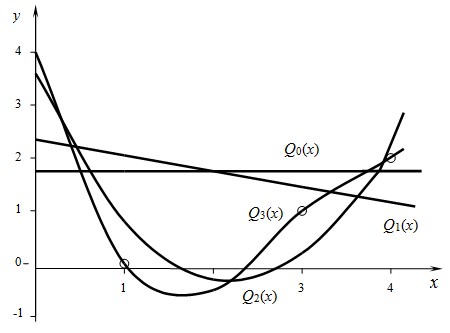
Рис. 1.
Эффективность использования аппроксимационных полиномов Чебышева подтвердилась при дальнейших исследованиях зависимости психофизиологической напряженности водителя от жесткости руля при надлежащем выборе числа экспериментальных точек.
Литература:
1. Леонова А. Б. Психодиагностика функциональных состояний человека. — М.: Изд-во Моск. ун-та. 1984. — 200 с.
2. Данилов А. М., Гарькина И. А. Сложные системы: идентификация, синтез, управление: монография. — Пенза: ПГУАС, 2011. — 308 с.







