В настоящее время появилась возможность решения математических задач без составления компьютерных программ. Причиной этого является разработка специальных математических программ — математических систем. В вузах и научных учреждениях чаще всего применяются математические системы: MathCAD, MATLAB, Maple, Mathematika. С применением математических систем учебный процесс становится интереснее, студенты понимают содержание занятия быстрее, глубже, а для укрепления преподаваемых понятий и решения задач остаётся больше времени.
Сейчас задачи вычислительной математики [1] по преимуществу решают в математической системе MathCAD [2–4]. Именно в MathCAD задача формулируется в наиболее естественном математическом виде, а в других математических системах шаги алгоритма решения задачи записываются с помощью команд системы.
В статье алгоритм конечно-разностной схемы Кранка-Никольсона приближённого решения линейного параболического дифференциального уравнения с краевыми условиями организованы в математической системе MathCAD.
1. Метод решения дифференциалных уравнений в MathCAD.
Пусть дана краевая задача для дифференциального уравнения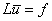 в непрерывной области D. Сопоставим ей некоторую дискретную задачу
в непрерывной области D. Сопоставим ей некоторую дискретную задачу 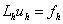 в дискретной области
в дискретной области 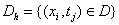 , которая состоит из узлов
, которая состоит из узлов 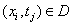 , с параметром дискретизации
, с параметром дискретизации 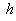 и
и 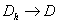 ,
, 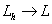 , при
, при 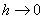 , где
, где 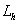 - дискретный оператор, а переменные
- дискретный оператор, а переменные 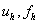 - дискретные функции, такие, что
- дискретные функции, такие, что 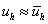 ,
, 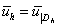 ,
, 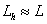 ,
, 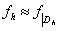 , т. е.
, т. е. 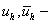 каркас –таблица значений функций
каркас –таблица значений функций 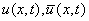 на сетке точек
на сетке точек 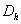 . В качестве дискретной задачи мы берем конечно-разностную схему (КРС), и тогда дискретная задача есть система алгебраических уравнений (СЛАУ). В MathCAD идея решения дискретной задачи
. В качестве дискретной задачи мы берем конечно-разностную схему (КРС), и тогда дискретная задача есть система алгебраических уравнений (СЛАУ). В MathCAD идея решения дискретной задачи 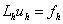 очень проста и естественна:
очень проста и естественна: 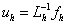 .
.
В MathCAD задачи решаются тремя способами [4]:
1) с помощью внутренних функций MathCAD;
2) с помощью математического алгоритма решения задачи;
3) с помощью алгоритма решения задачи, реализованного, во внутреннем языке MathCAD.
2. Дифференциалные краевые задачи и КРС [1].
А) Рассмотрим краевую задачу для параболического уравнения:
,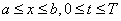 ,(1)
,(1)
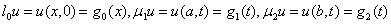 . (2)
. (2)
(1), (2) называется краевой задачей для параболического дифференциального уравнения (КЗ для ПДУ). Функция 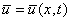 , удовлетворяющая ПДУ и краевым условиям называется точным решением:
, удовлетворяющая ПДУ и краевым условиям называется точным решением: 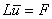 ,
, 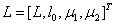 ,
, 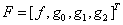 .
.
Явная КРС 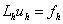 ,для ПДУ точности
,для ПДУ точности 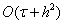 имеет вид:
имеет вид:
(3)
Чисто неявная КРС 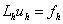 ,для ПДУ с точности
,для ПДУ с точности 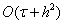 имеет вид:
имеет вид:
(4)
Схема Кранка-Николсона являетсяполусуммой явной и чисто неявнойсхем точности 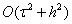 и имеет вид
и имеет вид
(5)
К (3) — (5) необходимо присоединить начальные и краевые условия
,(6)
Явная КРС для ПДУ на каждом слое j+1 решается с помощью реккурентных формул:
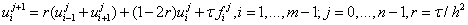 , (7)
, (7)
Неявная КРС для ПДУ на каждом слое j+1 сводиться к системе линейных уравнений:
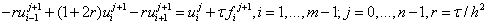 . (8)
. (8)
Чисто неявная КРС для ПДУ на каждом слое j есть система линейных уравнений с трёхдиогнальной матрицей и, начиная с первого слоя, решается методом прогонки.
Вводя матрицу 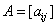 с коэффициентами
с коэффициентами 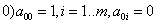 ;
;
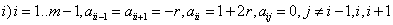 ;
; 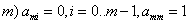 ,
,
и векторы 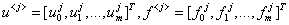 чисто неявную схему можно записать в векторно-матричном виде, связывающим неизвестные
чисто неявную схему можно записать в векторно-матричном виде, связывающим неизвестные 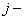 го и
го и 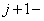 го слоёв
го слоёв
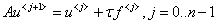 . (9)
. (9)
Вводя матрицы 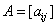 ,
,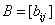 с коэффициентами
с коэффициентами
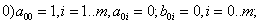
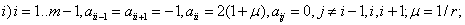
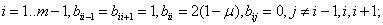
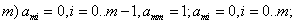 ,
,
и векторы 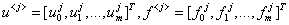 схему Кранка-Николсона можно записать в векторно-матричном виде, связывающим неизвестные
схему Кранка-Николсона можно записать в векторно-матричном виде, связывающим неизвестные 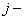 го и
го и 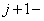 го слоёв
го слоёв
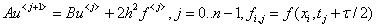 . (10)
. (10)
Подробно эту схему можно написать в виде (откуда получена КРС (10)):
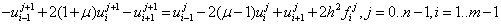 .
.
КРС (5) является частным случаем более общей КРС с весами [1]:
(11)
Для неё можно построить аналогичную СЛАУ (9).
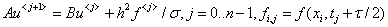 . (12)
. (12)
Это следует из равенств, которые получаются после преобразования (11):
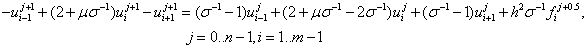
Отсюда, в частности 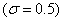 следует СЛАУ для КРС Кранка-Николсона.
следует СЛАУ для КРС Кранка-Николсона.
3. Организация решения КРС для ПДУ в MathCAD.
Пусть дана краевая задача для параболического уравнения (1),(2) с данными:
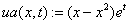 ,
,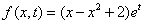 . (13)
. (13)
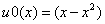 ,
, 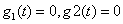 . (14)
. (14)
A) Решение с помощью внутренней функции Pdesolve.
Вводим в окне M следующие команды:
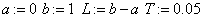 «область
«область
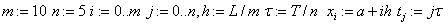 «сетка
«сетка
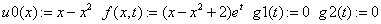 «начальные данные
«начальные данные
Given 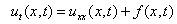 «ПДУ, равенство жирное
«ПДУ, равенство жирное
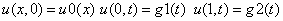 «краевые условия, равенство жирное
«краевые условия, равенство жирное
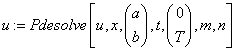
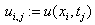 «обращение к Pdesolve
«обращение к Pdesolve
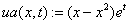
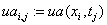 «решения
«решения 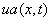 ,
,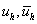
«выведем таблицу значений приближённого решения
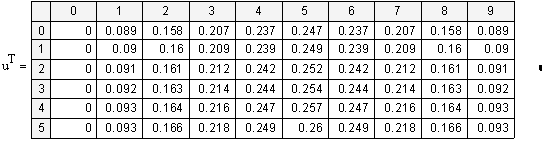
«выведем таблицу значений точного решения
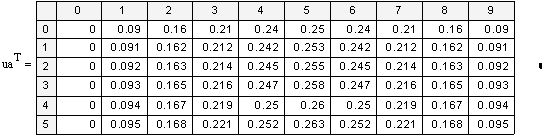
«выведем графики приближённого и точного решений
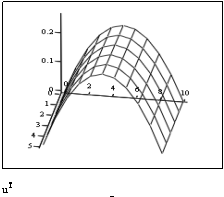
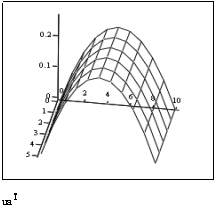
D) Решение КРС Кранка- Николсона для ПДУ в MathCAD.
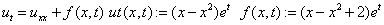
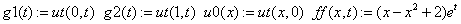
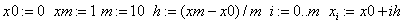
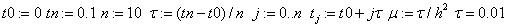
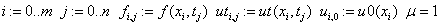
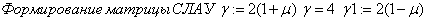
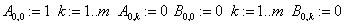
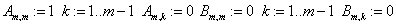
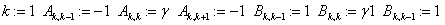
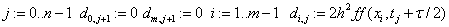
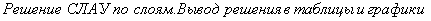
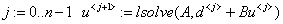
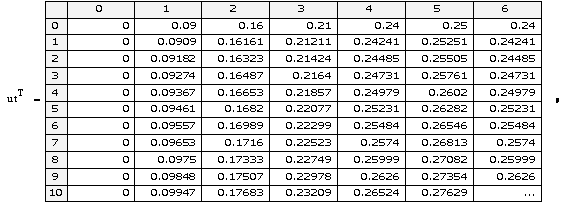
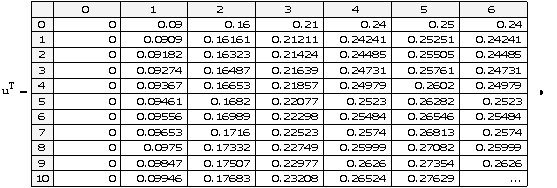
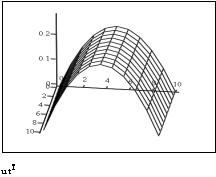
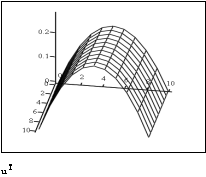
Результат КРС высокой точности налицо: разница встречается только на пятом знаке после запятой.
Литература:
1. Самарский А. А. Теория разностных схем. М.: Наука, 1977.-656 с.
2. Ракитин В. И. Руководство по ВМ и приложения MathCAD.М.:ФМ, 2005.-264 с.
3. Охорзин В. А. Прикладная математика в системе MathCAD. СПб, Лань,2008–352с.
4. Имомов А. Решение краевой задачи для линейных ДУ в частных производных в MathCAD. Молодой учёный, № 8(67), июнь 1, 2014 г.-с. 6–12







