В работе рассмотрены вопросы по существующим проблемам при перевозке мелких партий груза, составление и расчет наиболее рациональных маршрутов, которые приводят к снижению холостого пробега, транспорта и позволяет сократить транспортные издержки на перевозимый груз.
Ключевые слова: маршрутизация, мелкопартионные грузы, графы, матрицы, планирование маршрутов.
Проблемы при перевозке готовой продукции для предприятия заключается в отсутствии рассчитанного, составленного, рационального маршрута движения, с учетом всех факторов воздействующих на транспортный процесс.
Маленькие партии груза это сборные грузы, то есть по объему не превышающие тысячи килограмм, которые необходимо перевезти в одном направлении, но для разных получателей.
Планирование грузопотоков в транспортных системах основывается на определении рационального объема и направлении перевозок. Грузопоток представляет собой некоторое количество грузов, которые транспортируются в определенном направлении за установленный период времени [1, с. 5].
Если является необходимым перевезти груз, то здесь просто необходимым элементом является автотранспорт, его высокая мобильность и маневренность позволит с легкостью доставить груз в нужные сроки.
Для того, чтобы мелкие заказы доставить до потребителя чаще всего используется малотоннажный автомобиль — грузоподъемность данного авто от 1,5 до 3 тонн
При перевозке продукции до потребителей могут возникать следующие проблемы, а именно заторовые состояния, сложность транспортной системы города не всегда позволяет выбрать наиболее удобный маршрут, ограниченное количество времени при доставке и форс-мажорные обстоятельства.
Суть задачи маршрутизации мелких партий груза заключается в том, что необходимо построить оптимальные маршруты, при которых:
- загрузка транспортного средства не должна превышать его грузоподъемности;
- сума общего пробег транспортного средства по маршрутам должен быть наиболее минимальна;
- обеспечить наибольшую производительность подвижного состава на действующем маршруте;
- обеспечить минимизацию транспортных издержек.
Быстро и эффективно задачи выбора способов маршрутизации можно решить лишь с помощью математических методов. Например, по отношению к автомобильному транспорту методом линейного программирования можно:
- отыскивать оптимальное количество ездок автомобилей на маршрутах при установленном времени пребывания в наряде (задачи на минимизацию потерь рабочего времени);
- определять оптимальные варианты продвижения однородных грузопотоков от источников их генерации до пунктов назначения (задачи на минимизацию транспортных затрат);
- разрабатывать оптимальные стратегии по ориентации перевозчиков на определенную группу клиентов (на выделенный сегмент рынка логистических услуг). В этом поможет решение задач по минимизации нулевых пробегов;
- составлять рациональные маршруты работы подвижного состава с позиций увязки намечаемых ездок (задачи по минимизации холостых пробегов);
- выделять рациональные «развозочные» и «сборочные» маршруты (задачи на определение минимальных пробегов при объезде обусловленных грузопунктов);
- эффективно распределять транспортные и погрузочно-разгрузочные средства по маршрутам логистических цепей (задачи на максимальное использование рабочего времени автомобилей и рабочего времени погрузочно-разгрузочных механизмов.) [1, с. 7].
Основной целью проектирования маршрутов на предприятии молокозавода является сокращение затрат и обеспечение потребителей свежей продукцией.
Движение подвижного состава происходит по маршрутам. Маршрут движения — путь следования автомобиля при выполнении перевозок.
Маршруты движения могут быть двух типов:
- маятниковые, когда продукция развозиться несколько раз одному и тому же потребителю
- кольцевые, когда продукция развозиться нескольким потребителям за одну ездку.
Маршрутизация перевозок это наиболее эффективный способ организации оптимального продвижения грузопотоков по логистическим каналам и цепям. Основание рациональных маршрутов позволяет точно определить объемы перевозимых грузов в территориальном и временном разрезе, рассчитывать необходимое количество транспортных средств для обеспечения грузопотоков, добиваться значительного снижения простоев подвижного состава под погрузкой и разгрузкой [2, с. 123].
При расчете маршрутов используется математический метод для организации материалопотока. Применение математических методов и моделей в логистике необходимо в тех случаях, когда проблема сложна, и решить ее простейшим методом на основе опыта работы невозможно. В таких случаях необдуманное и не проанализированное решение может привести к серьезным последствиям.
Использование математического метода, позволяет логисту осуществить выбор наиболее близких к ним вариантов решений по определенным критериям и рассчитать наиболее рациональный маршрут для перевозки продукции [3, с. 22].
На этапе построение математической модели записываются в виде математических формул (функций, неравенств, уравнений и т. д.) соотношения между выделенными факторами, влияющие на решение проблемы.
При этом эти зависимости должны удовлетворять сформулированным гипотезам и известным свойствам исследуемого процесса. Сложность модели должна быть таковой, чтобы она поддавалась анализу и численному расчету и могла бы быть информационно обеспечена.
Поэтому на этом этапе возможны некоторые упрощения ситуации. Необходимо заботиться о том, чтобы эффект от дополнительной информации был большим по сравнению с затратами на ее получение. Чтобы правильно построить граф необходим специалист очень хорошо знающий движение в городе, и математика, имеющего опыт формализации различных зависимостей и связей между элементами систем.
Множество всех дорог города составляет дорожную сеть. В ней учитываются только те дороги, которые пригодны для движения по ширине проезжей части и качеству покрытия. Также специалист должен учитывать все возможные зоны улично-дорожной-сети на наличие опасных участков. Модель такой сети может быть представлена в виде графа (рисунок 1).
Граф — это фигура, состоящая из точек вершин и отрезков, их соединяющих. Для составления графа используется картографический материал региона или населенного пункта, отражающий все существующие магистрали движения, улицы, проезды, а также организацию дорожного движения и существующие ограничения [4, с. 23]. Как видно из рисунка 1, часть ребер ориентирована по направлению. Такие ребра называются дугами. В зависимости от того, все или часть ребер имеют направление, граф является ориентированным или смешанным.
Рис. 1. Граф, модель транспортной сети
Для того, чтобы построить граф, необходимо построить кратчайшую сеть, связывающую все пункты без замкнутых контуров («минимальное дерево») рисунок 2.
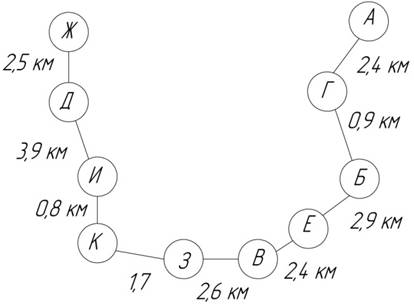
Рис. 2. Минимальное дерево
Граф чаще всего является смешанным, так как в городских условиях на некоторых улицах установлено одностороннее движение. Для моделирования транспортной сети, прежде всего, необходим картографический материал. Граф должен быть достаточно подробным, отображать нынешнее состояние города (района).
На развозочном маршруте автомобиль загружается в одном пункте и развозит продукцию нескольким потребителям, обслужив потребителей, порожним возвращается в первоначальный пункт маршрута.
Таблица 1
Группировка маршрута исходя из грузоподъемности автомобиля
|
Маршрут 1 |
Маршрут 2 |
||
|
Обозначение |
Объём завоза, кг |
Обозначение |
Объём завоза, кг |
|
Г |
120 |
К |
260 |
|
Д |
240 |
З |
190 |
|
Ж |
320 |
Е |
240 |
|
И |
320 |
В |
210 |
|
Б |
100 |
||
|
Итого: |
1000 |
Итого: |
1000 |
Сгруппировав пункты по маршрутам исходя из наиболее отдаленных потребителей, переходим к следующему этапу расчетов. Определяем рациональный порядок объезда пунктов каждого маршрута. Для этого строим таблицу-матрицу.
Таблица 2
Матрица расстояний для маршрута 1
|
Номер строки в матрице |
А |
2,4 |
2,6 |
5,1 |
6,5 |
|
1 |
2,4 |
Г |
0,2 |
2,7 |
5,1 |
|
2 |
2,6 |
1,2 |
Д |
2,5 |
3,9 |
|
3 |
5,1 |
2,7 |
2,5 |
Ж |
1,4 |
|
4 |
6,5 |
5,1 |
3,9 |
1,4 |
И |
|
∑ |
16,6 |
10,4 |
9,2 |
11,7 |
16,9 |
Начальный маршрут строим для трех пунктов матрицы, имеющих наибольшие размеры сумм, показанных в строке «сумма» (16,9; 16,6; 11,7), т. е. А, И и Ж. Для включения последующих пунктов выбираем из оставшихся пункт, имеющий наибольшую сумму, например, пункт Г (сумма 10,4), и решаем, между какими пунктами его следует включать, т. е. между А и И, И и Ж или Ж и А. Чтобы это решить, для каждой пары пунктов необходимо найти размер приращения маршрута по формуле
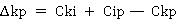 , (1)
, (1)
где С — расстояние, км (табл. 3); i — индекс включаемого пункта; k — индекс первого пункта из пары; р — индекс второго пункта из пары [1, с. 17].
При включении пункта Г между первой парой пунктов А и И определяем размер приращения ∆АИ при условии, что
i = Г; k =А; р = И.
Тогда ∆АИ = САГ + СГИ — САИ.
Подставляем значения из таблицы 3, получаем, что;
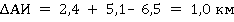
Таким же образом определяем приращение ∆ИЖ (если пункт Г включить между пунктами И и Ж) и ∆ЖА, если Г включить между пунктами Ж и А:
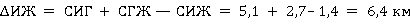 ,
,
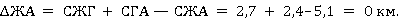
Из полученных значений приращений (∆АИ = 1,0 км; ∆ИЖ = 6,4 км и ∆ЖА = 0 км) выбираем минимальное, т. е. ∆ЖА = 0. Следовательно, Г должно быть между пунктами А и И. Маршрут получает вид А — Г — И — Ж — А.
После чего для оставшегося пункта повторяем ход действий и производим расчет для оставшегося наименьшего пункта. Таким образом, после решения данных примеров вырисовываются маршруты, которые можно отобразить на графе, а после отражать на карту города.
На практике данный метод был применен на молокозаводе для построения рациональных маршрутов. Так как область развоза продукции определяется чертой города, то данный метод организации транспортного процесса мелких партий груза помог решить основную проблему, сокращение транспортных средств осуществляющих эти перевозки, что позволило сократить транспортные издержки на одну тонну перевезенного груза. Основной проблемой на предприятии являлся простой транспорта во второй половине дня, отсюда появилась еще одна проблема отсутствие свежей продукции на прилавках магазинов т. к. продукция развезенная в первой половине дня изготавливалась и маркировалась вчерашним днем то завод нес, убытки в этом плане. Для устранения данной проблемы нами было принято решение, разработки рационального маршрута для перевозки во второй половине дня, этим мы исключили простой транспорта во второй половине дня, и возможность обеспечивать потребителей свежей продукцией выпущенной в первой половине дня. Данными мероприятиями мы усовершенствовали транспортный процесс на предприятии и повысили конкурентные преимущества завода, что привело к увеличению прибыли.
После расчетов получаются маршруты, рассчитанные математическим методом, которые готовы к применению на предприятии.
Научная новизна заключается в том, что:
- предложенная математическая система поиска выгодных маршрутов, отличающаяся совместным использованием стандартных математических приемов, позволяет делать четкий вывод, что позволяет находить оптимальные по критерию времени маршруты;
- позволяет не дожидаться полной загрузки автомобиля, а выполнять перевозку продукции по временным интервалам;
- сведение к использованию по минимуму грузовых транспортных средств.
Данная программа по расчету рациональных маршрутов имеет дальнейшие возможности и перспективы по расчетам наиболее сложных маршрутов с использованием большого количества автотранспорта и увеличению масштабов перевозок.
Литература:
1. Романова. Т. И. Логистика. Методические указания к практическому занятию. Томск: Изд-во Том. Гос. Архит.- строит. Ун-та, 2009. — 22 с.
2. Неруш. Ю. М. Логистика: учеб. — 4-е изд-во Проспект., перераб. и доп. — М.: Т.К Велби, Проспект, 2006. — 520 с.
3. Неруш Ю. М. Практикум по логистике: учебное пособие, ТК Велби, Проспект, 2008. — 452 с.
4. Пархоменко В.И Транспортная логистика и транспортные средства: Конспект лекций, Павлодар, 2008. — 103 с.







