Генетические корреляции — особый тип корреляций, используемых для выяснения генетических причин связи между количественными признаками потомков и родителей — играют важную роль в оценке генотипа, однако, определение их представляет некоторые сложности, поскольку до настоящего времени нет однозначных методов определения их количественных значений через устоявшиеся статистические константы популяционной генетики. Предложенные Хейзелем [1] четыре выражения для определения этого показателя во-первых дают совершенно разные результаты, а во-вторых имеют место случаи когда значения коэффициентов генетической корреляции превосходит ±1. По предлагаемым формулам (1), (2), (3), (4) теоретически, он может лежать в пределах от минус до плюс бесконечности, что исключает само понятие корреляции, и кроме того, эти результаты часто невозможно интерпретировать, поскольку они нередко бывают мнимыми. Это несложно заметить при анализе формул:
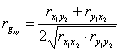 , (1)
, (1)
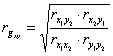 , (2)
, (2)
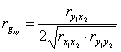 , (3)
, (3)
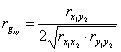 (4)
(4)
где rx1y2, ry1x2, rx1x2, ry1y2 — коэффициенты парной корреляции признаков потомков и предков. Индексы -1, 2, x, y обозначают: 1 и 2, номера признаков х — потомка, y — предка.
Отдельные авторы [2] для устранения таких явлений рекомендуют увеличение объема исследуемой совокупности, но с одной стороны это не обязательно меняет ситуацию, а с другой, — не всегда возможно.
С нашей точки зрения наиболее вероятная причина этого в неудачном выборе способа определения генетических корреляций. Такое заключение сделано на основании анализа нескольких сотен вычисленных корреляций по всем четырем формулам Хейзеля. Число удовлетворительных значений (т. е. вещественных, не выходящих за пределы ± 1) не превышает и половины от общего количества. Предлагаем использовать для этой цели математический аппарат частных корреляций признаков предков и потомков.
По определению частные корреляции показывают степень чистого взаимовлияния пары признаков, при фиксированном значении остальных. Величина частной корреляции, так же как и обычной-парной, колеблется в пределах от минус единицы при обратной функциональной связи до плюс единицы — при прямой, включая все промежуточные значения, где эта связь не является функциональной. При трех взаимосвязанных факторах x,y,z коэффициент частной корреляции rxy(z)(коэффициент частной корреляции первого порядка между xи y при фиксированном значении z) определяется через обычные парные корреляции выражением [3]
![\includegraphics[.22in,.97in]{D:/html/work/link1/metod/met90/met9062.eps}](https://moluch.ru/blmcbn/10960/image005.png) (5)
(5)
Количество одновременно учитываемых факторов — m (в формуле (5) m = 3, т. е. x,y,z) определяет порядок р частной корреляции соотношением p = m — 2, при этомобычные парные корреляции считаются частными корреляциями нулевого порядка.
Формулы определения частных корреляций высших порядков через низшие (рекурентные формулы) подобны (2), но громоздкость их столь быстро растет с увеличением числа факторов, что в практическом плане они малоприменимы. Для этой цели разработан ряд альтернативных методов вычисления частных корреляций высших порядков, основанных на теории множественных корреляций и регрессий.
(рекурентные формулы) подобны (2), но громоздкость их столь быстро растет с увеличением числа факторов, что в практическом плане они малоприменимы. Для этой цели разработан ряд альтернативных методов вычисления частных корреляций высших порядков, основанных на теории множественных корреляций и регрессий.
Дж. Юл и Э. Кендэл[4] показали возможность определения частных корреляций порядка т через β-коэффициенты стандартизированных уравнений множественной регрессии того-же порядка:
r1,2.3,4...m=(β1,2.3,4...m * β2,1.3,4...m)0,5 (6)
М.Эзекиэл и К. Фокс [4] предложили способ определения частных корреляций порядка m через множественные корреляции порядка m и m — 1.
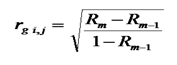 (7)
(7)
ЗдесьRm коэффициент множественной корреляции результативного признака и m факториальных признаков. Rm–1 — то же, с исключенным факториальным признаком для которогоопределяется частная корреляция.
Формулу Эзекиэла-Фокса, наиболее понятна и удобна для формализации при разработке алгоритма вычисления генетических корреляций. Множественные корреляции Rmопределяются из соотношения [5]:
 (8)
(8)
Где β — корни системы (6) из m (число факториальных признаков для которых определяются частные корреляции) уравнений с m неизвестными β, ry,I — коэффициенты парной корреляции очередного результативного фактора с каждым факториальным признаком. Коэффициентами неизвестных системы уравнений служат элементы матрицы всех парных корреляций факториальных признаков между собой [5].
 (9)
(9)
Для определения полной матрицы генетических корреляций нескольких признаков потомков и предков описанным методом, в качестве исходных данных необходимы две корреляционные матрицы: полная корреляционная матрица между всеми признаками потомков (элемент матрицы ri,j) и всеми признаков предков со всеми признаками потомков (элемент матрицы ry i,j). Если, для конкретности, принять m=3, то исходные корреляционные матрицы будут иметь следующий вид:
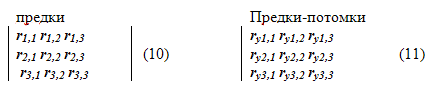
Исходя из вышеизложенного, алгоритм определения элементов матрицы генетических корреляций представляет следующую последовательность действий.
1. Циклический создается система (9), в которой квадратной матрицей служит матрица парных корреляций признаков предков (10), а матрицей-столбцом поочередно принимаются столбцы матрицы (11) с номером признака, для которого определяется строка матрицы генетических корреляций (12).
2. Решается система (9) и вычисляется по формуле (8) текущее значение Rm.
3. В текущей системe (9), в матрице (10) и текущем столбце свободных членов, циклически поочередно вычеркивается строка и столбец с номером текущего признака и решением оставшейся системы (m — 1) порядка, вычисляется по формуле (8) текущее значение R m — 1.
4. Вычисляется по формуле (7) значение текущего элемента матрицы частных корреляций (12) индекс строки которого определяется номером столбца в пункте 1, а индекс столбца — номерами строки и столбца, которые вычеркиваются, в пункте 3.
Процесс повторяется до полного заполнения матрицы генетических корреляций (12).. По окончании процесса будет получен полный набор генетических корреляций
|
Потомки |
Предки |
|
r g 1,1 r g 1,2 r g 1,3 |
|
|
r g 2,1 r g 2,2 r g 2,3 |
(12) |
|
r g 3,1 r g 3,2 r g 3,3 |
Проиллюстрируем определение генетических корреляций между 15 потомками барана-производителя UA6500003076 украинской мясо-шерстной породы.
Исследовалась взаимосвязь трех селекционируемых признаков: 1) длина волокна в возрасте 1 года (см.), 2) живая масса в возрасте 1 года (кг.), 3) настриг шерсти в возрасте 1 года (кг) потомков и их матерей, исходные корреляционные матрицы (10), (11) которых следующие:

В результате выполнения пунктов 1- 4 алгоритма расчета, получена матрица генетических корреляций (15) любого из трех селекционируемых признаков потомков отца UA6500003076 с каждым селеционируемым признаком их матерей.
Обращает на себя внимание то, что элементы матриц (14) и (15) разнятся не только по модулю но, в отельных случаях, даже знаком, хотя, по существу, являются
|
Потомки |
Матери |
|
0.662 -0.007 0.487 |
|
|
0.285 0.386 -0.335 |
(15) |
|
0.493 0.317 0.158 |
мерой одной и той же величины — взаимосвязи между двумя селекционируемыми признаками потомков и их матерей. Так взаимосвязь между настригом шерсти потомков и живой массой матерей определенная коэффициентом парной корреляции ry3,2 =-0.163 — небольшая отрицательная связь (14), показывающая, что в среднем, у более крупных матерей рождались потомки с меньшим настригом чем у их сверстников рожденных от матерей с меньшей массой. Коэффициент генетической корреляции
rg3,2 =0.317 (15), показал, что дело обстоит как раз наоборот и это не противоречит здравому смыслу, поскольку у крупных родителей вероятнее рождение более крупных потомков, со всеми вытекающими последствиями. Теоретически это объясняется тем, что в матрице (14) взаимосвязь определялась с помощью парных корреляций при скрытом влияние остальных признаков. Генетические корреляции определяют эту величину при элиминировании остальных, что дает возможность определить истинную зависимость одной случайная переменная величина от другой. Знание реальной ситуации, поможет избежать ошибочных направлений в селекции. Генетические корреляции используются так же для оценки биологических объектов по комплексу признаков с помощью селекционных индексов.
Таким образом, обоснована теоретически и показана на практическом примере возможность и целесообразность использования способа частных корреляций при расчете генетических корреляций для использования их в биологических исследованиях.
Литература:
1. Шталь В., Раш Д., Шилер Р., Вахал Я. Популяционная генетика для животноводов-селекционеров / В. Шталь — М.: Колос, 1973. — 439 с.1. Шталь В., Раш Д., Шилер Р., Вахал Я.
2. Тейнберг P. P. О возможности применения селекционных индексов при селекции молочного скота // Генетика. 1971. Т. 7. № 5. С. 62–68.
3. Вычисление частного коэффициента корреляции http://cito-web.yspu.org/link1/metod/met90/node24.html
4. Юл Дж. Э., Кендэл М. Теория статистики. М.: Гос- статиздат, 1960. С. 326–331.
5. ЭзекиэлМ.,Фокс К. Методы анализа корреляций и регрессий. М.: Статистика, 1966. С. 203–213.







