Рассматривается вопрос об использовании функции влияния, являющейся аналогом функция Грина, в некоторых прикладных задачах механических систем типа стильтьесовской струны. Для некоторых типов таких задач приведен анализ в случае сингулярных особенностей, возникающих в виде производных от скачков. оответствующих сосредоточенным в концевых узлах усилиям и упругим опорам. Функцию Гри́на (или функция влияния) применяют для различных решений неоднородных краевых задач. Также она используется в теории конденсированных сред, в электростатике. квантовой механике. Эта функцияиспользуется в различных конструкционных задачах.
В военно-технических прикладных задачах нередко возникают механические системы из струн и тросов, вдоль которых распределены сосредоточенные нагрузки. Примерами таких механических систем являются электропровода между опорами линий электропередач, тросы канатных мостов и некоторые другие. Такие системы называют стилтьесовскими струнами. Расчет и анализ формы и сил реакции этих упругих струн с распределенными вдоль них внешними нагрузками представляет сложную задачу, актуальную как с прикладной, так и с теоретической точек зрения.
Для таких расчетов изучены новые методы математического моделирования, использующие свойства функции влияния. В условиях достаточно регулярных сред, допускающих использование процедур дифференцирования и аппарата математической физики, функция влияния в канонических ситуациях совпадает с функцией Грина — важнейшим средством математического моделирования. С давних времен функция влияния, которую также называют иди функцией источника, функцией отклика, стала у физиков одним из наиболее эффективных средств описания взаимосвязи различных объектов и явдений. В начале XX века в задачах математической физики функция влияния приобрела вид функции Грина, введенной сначала для задачи Штурма-Лиувилля. Далее понятие функции Грина было распространено на более общие задачи старших порядков, а теория была развита на основе аксиоматического подхода к определению самой функции Грина, который крайне затруднил анализ конкретных физических задач.
Оператор Шредингера, оказался востребован в середине XX века для анализа в случае сингулярных особенностей потенциала, возникающих в виде, например, производных от скачков, называемых по физической терминологии дельта-функциями. На чисто описательном уровне математическую постановку соответствующей задачи удалось осуществить с помощью создания для этого теории обобщенных функций распределений Шварца-Соболева. Подобный обобщенный подход не позволял провести достаточно глубокий анализ, не приближая математические выкладки к физически интерпретируемым свойствам той же функции влияния. Причиной сложившейся ситуации являлось то, что для дифференциальных уравнений с обобщенными коэффициентами отсутствовала какая-либо параллель с классическими теоремами анализа с поточечным дифференцированием.
Сравнительно недавно доступ к поточечному анализу задачи с обобщенными коэффициентами был разработан путем распространения на дифференциальные уравнения производных типа Радона-Никодима из общей теории интегралов. Для этого используется нетрадиционный для математической физики интеграл Стилтьеса, а описание напряженного состояния объекта осуществляется не привычным для математической физики дифференциальным уравнением второго порядка, а интегро-дифференциальным уравнением. При анализе спектральной функции «стильтьесовской струны» возникает уравнение вида
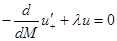(1)
как формальная запись соотношения
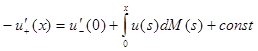(2)
Через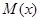 
здесь обозначена неубывающая на отрезке 
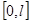функция, определяющая распределение масс. Интеграл в (2) понимается по Лебегу-Стильтьесу. Псевдопроизводная 
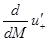вводится, например, при анализе задачи рассеяния (распространения тепла) и определяется не соотношением типа (2), а с помощью предельных переходов в конечноразностных отношениях. Через 
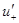в уравнениях (1) и (2) обозначена правая производная.
Рассмотрим более общее, чем (2), уравнение
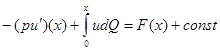(3)
При анализе данного уравнения возникает определенная сложность в виде неоднозначной определенности интегрального слагаемого в левой части. Если в некоторой точке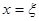 
функция 
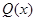имеет скачок, то интеграл не имеет собственного значения, а лишь предельное значение слева 
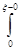и предельное значение справа, т. е. при 
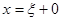. Поэтому равенство (3) вместе со всеми его компонентами, включая и 
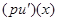, распространим на множество 
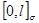. Данное множество получается из сегмента 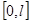с помощью замены каждой точки 
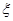разрыва 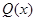парой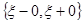 
.
Уравнение (3) основными свойствами похоже на обыкновенное дифференциальное уравнение второго порядка. Справедливы следующие утверждения. Пусть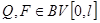 
, т. е. пространству ограниченной вариации.
Теорема 1. Для любых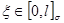 
и 
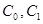начальная задача
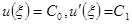
однозначно разрешима. К ее решению равномерно сходится процесс итераций
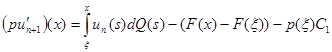
при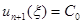 
, начатый с любой начальной функции 
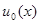из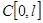 
. Это решение непрерывно зависит как от начальных условий, так и от 
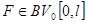(пространства функций с ограниченной вариации).
В данной теореме через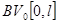 
обозначили множество функций из 
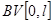с нулевым значением при 
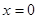. Заметим, что если 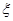— точка разрыва 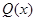, то исходную задачу можно разложить на две разные начальные задачи — левостороннюю в точке 
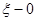и праввостороннюю в точке 
.
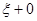Теорема 2. Пусть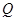 
не убывает. Тогда уравнение (3) при краевых условиях
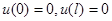, (4)
соответствующих глухому закреплению концов стильтьесовской струны, однозначно разрешимо для любой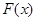 
из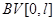 
. Для каждой неубывающей 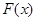это решение неотрицательно.
С механической точки зрение неубывание 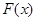означает, что к изучаемому объекту приложена неотрицательная во всех точках сила, включая также импульсы. Для данной задачи может быть построена функция влияния.
Рассмотрим общую струну с закрепленными концами (4). Эти условия исключают скачки на концах у функци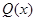й и 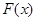. Действительно, эти скачки соответствуют сосредоточенным в концах усилиям и локальным упругим опорам типа пружин, которые ввиду закрепления концов очевидно неуместны. Тогда в (3) интеграл должен браться от точки 
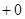, т. е. по интервалу 
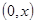. Покажем, что для данной задачи может быть построена функция влияния. Предположим всюду далее, что 
.
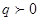Пусть в точке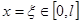 
приложена единичная сила. Это значит, что в (4) первое слагаемое имеет вид 
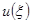, что соответствует функции
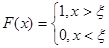
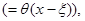
где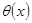 
— классическая функция Хевисайда. При этой 
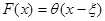уравнение (3) наверняка имеет решение, удовлетворяющее условиям (4), о чем утверждает следующая теорема.
Теорема 3 При неубывающей 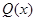для любой 
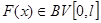краевая задача
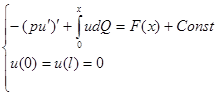(5)
однозначно разрешима.
При доказательстве использовались выше сформулированные теоремы, в силу которых однородная задача (5) при 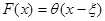имеет только тривиальное решение, и воспользоваться стандартной альтернативой Фредгольма.
Согласно теореме 3 задача (3),(4) имеет единственное решение. Обозначим его через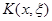 
.
Теорема 4. Для любой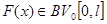 
решение задачи (3),(4) может быть представлено в виде
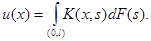
Последняя формула означает, что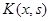 
является функцией Грина задачи (5).
Литература:
1. Аткинсон Ф. Дискретные и непрерывные граничные задачи. М.: Мир, 1968, 750 с.
2. Владимиров В. С. Уравнения математической физики. М.:Наука, 1967, 436 с.
3. Покорная О. Ю. О ядре несамосопряженных операторов. Материалы XLV1 отчетной научной конференции ВГТА, Воронеж, 2008, Ч.2, с.150.
