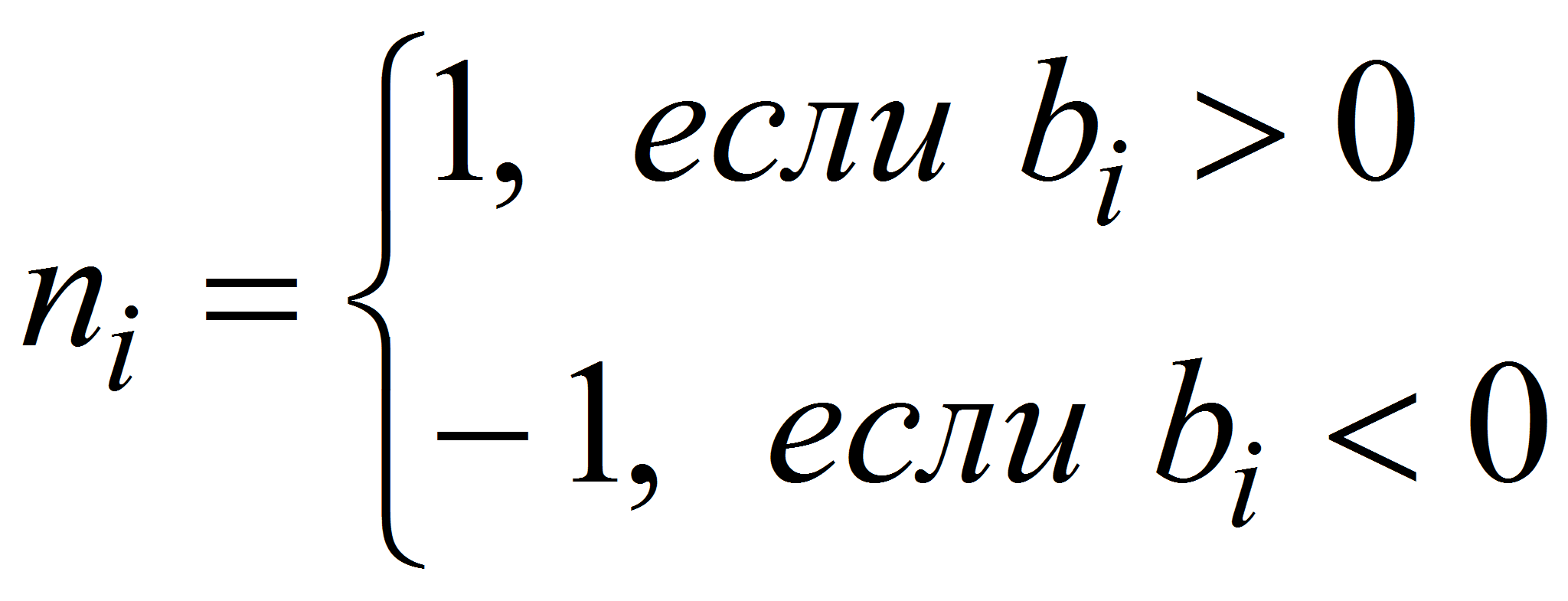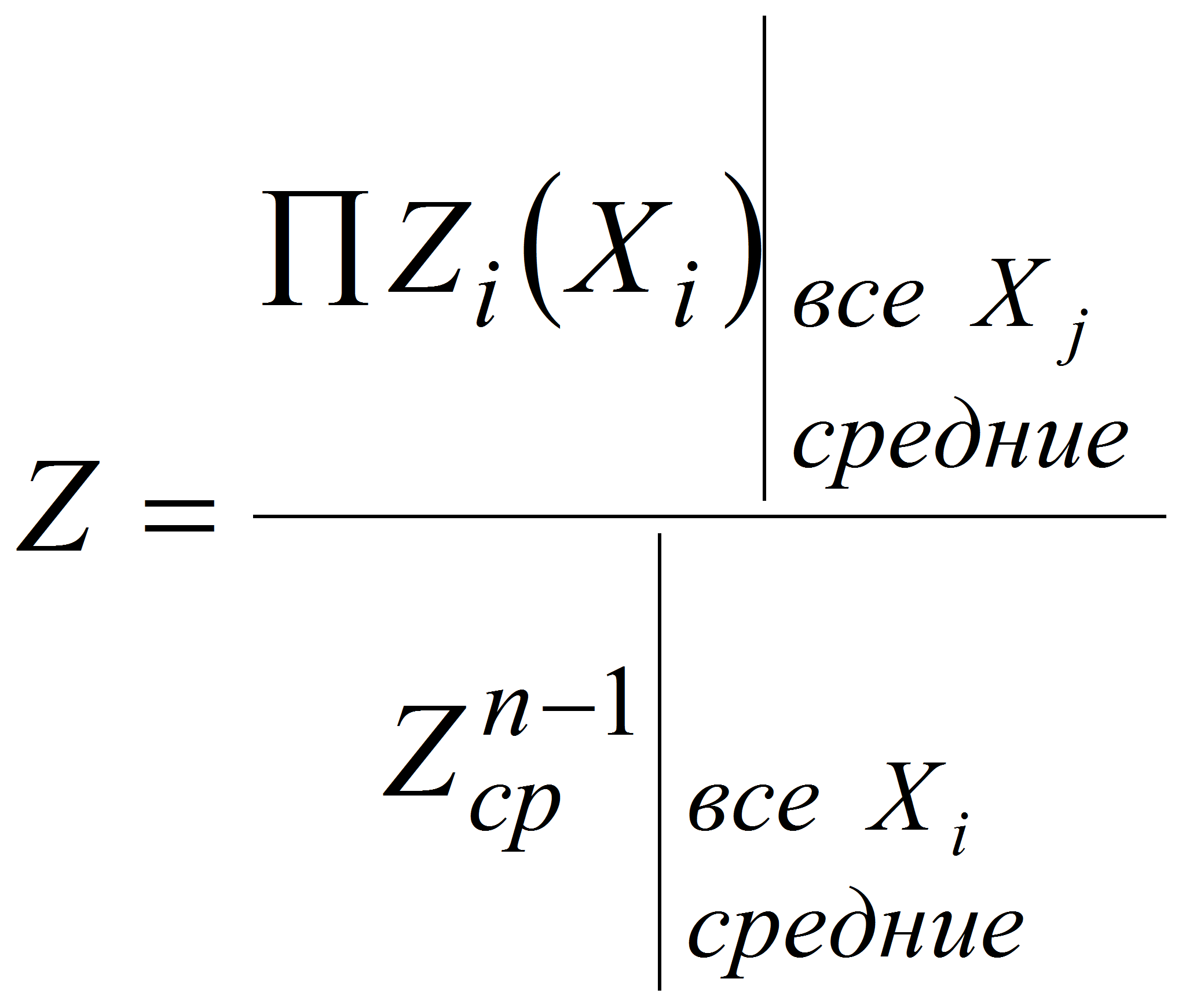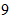Как правило, в ходе большинства научных исследований приходится сталкиваться с тем или иным видом экспериментов, он может проводиться на производстве, в лабораториях, на опытных участках и т.д. Эксперимент по своей сущности может быть как физическим, так и модельным.
В последнее время наряду с физическими моделями широкое распространение получили абстрактные математические модели. Данная работа посвящена разработке и исследованию математических моделей объекта исследования, в частности двигателя и его узлов.
Приоритетное внимание уделяется поиску оптимальных условий. Такая цель является одной из наиболее распространенных научно-технических задач. Подобные задачи возникают в тот момент, когда установлена возможность проведения процесса и необходимо найти наилучшие (оптимальные) условия его реализации. В широком смысле подобные задачи носят название задач оптимизации, а процесс их решения – процесс оптимизации (или просто оптимизация).
Многообразие условий применения авиационных ГТД в силовых установках летательных аппаратов и многочисленность показателей качества двигательных установок крайне усложняет задачу выбора оптимальных параметров рабочего процесса авиационного двигателя. При выборе параметров рабочего процесса конструктору необходимо одновременно удовлетворить большое количество требований, как правило, противоречивых с позиции их возможной реализации.
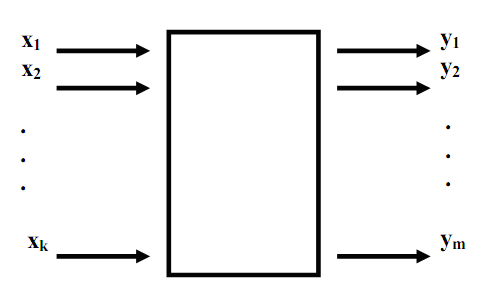
Рассмотрим обычную схему – «черный ящик», служащую для описания объекта исследования, приведенную на рисунке 1. Справа изображены стрелки, обозначающие численные характеристики целей исследования, любые из этих характеристик могут использоваться в качестве параметров оптимизации (в зависимости от целей поставленной задачи). Параметры оптимизации в литературе зачастую называют также критериями оптимизации, целевой функцией, выходом «черного ящика» и т.д.
Соответственно для проведения исследований и экспериментов, необходимо иметь возможность воздействовать на результаты «черного ящика». Способы такого воздействия называют факторами оптимизации (или входами «черного ящика»), они условно изображены стрелками слева на рисунке 1.
Рис. 1. Общая схема «черного ящика»
При решении любой оптимизационной задачи используются математические модели исследования, при этом под математической моделью понимается уравнение, связывающее параметр оптимизации с факторами на него воздействующими. В общем виде это уравнение можно представить как:
где φ(x1) функция отклика.
При разработке программного обеспечения используется принцип воздействия на «черный ящик» – при закрытых алгоритмах работы того или иного приложения выявлять функции отклика, для дальнейшего анализа.
В настоящее время промышленные предприятия имеют в своем арсенале много программных средств, представляющих собой DOS-приложения, с консольным управлением, что делает работу с ними достаточно сложной для рядового пользователя. Однако отказаться от них нет возможности, так как они используют уникальные методы расчета, воспроизведение которых потребует больших временных затрат и других издержек.
Таким образом, использование программ-оптимизаторов даст "вторую жизнь" устаревшим DOS-приложениям, которые станут играть роль решателей.
В разработке настоящего программного обеспечения сделан акцент на унификацию его применения. Предполагается объектно-ориентированный интерфейс для оперирования параметрами оптимизации - такое представление будет более интуитивным для пользователя. И позволит работать с подавляющим большинством DOS-приложений без привлечения сторонних специалистов для адаптации программного комплекса по оптимизации к тому или иному решателю.
Разрабатываемый программный комплекс базируется на следующих основных принципах:
- высокая эффективность решения для сложных многопараметрических задач, которая позволит существенно сократить сроки их решения;
- простота использования процедур оптимизации. Она достигается реализацией адаптивных алгоритмов, не требующих предварительных настроек и задания параметров, что позволит их использовать специалистам, не владеющим специальными знаниями в теории оптимизации.
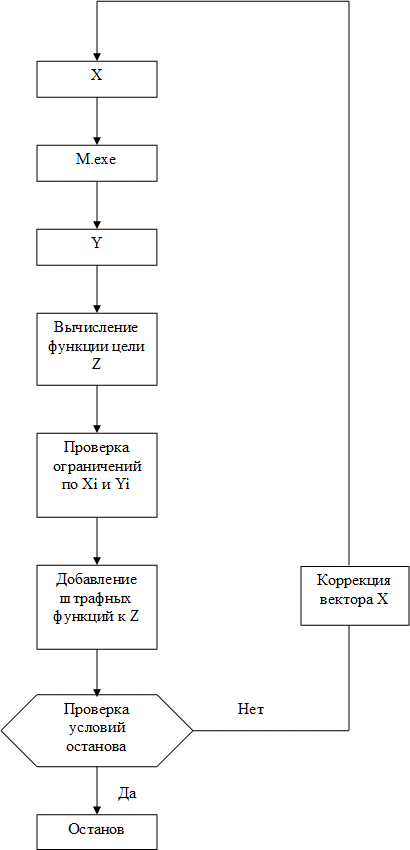
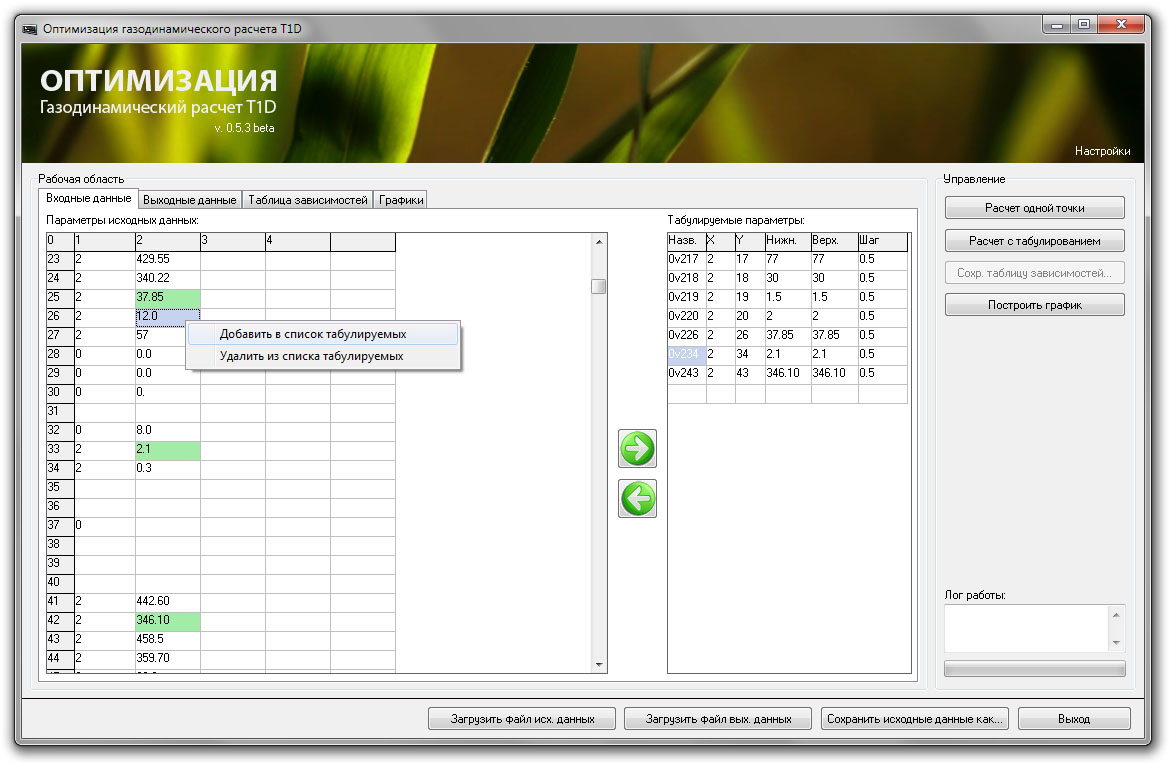
Блок-схема работы разрабатываемого программного комплекса показана на рисунке 2. Для некоторой модели, заданной «черным ящиком» в виде исполняемого файла M.exe, факторы X задаются файлом входных данных (пример импорта исходных данных и выбор табулируемых параметров приведен на рисунке 3), а результаты расчета записываются в файл Y (пример приведен на рисунке 4). Поиск оптимума представляет собой «оптимальное управление», когда внешняя программа (назовем ее «оптимизатор») заставляет модель M двигаться из исходного состояния X0(X10, X20… Xk0) в конечное Xн(X1н, X2н… Xkн), функция цели при этом имеет вид:
где
![]() - начальное значение некоторого выходного параметра,
- начальное значение некоторого выходного параметра,
![]() - весовые коэффициенты выходных параметров, при чем
- весовые коэффициенты выходных параметров, при чем
![]() если
если
![]() минимизируемый параметр;
минимизируемый параметр;
![]() если
если
![]() максимизируемый параметр,
максимизируемый параметр,
i – номер итерации.
На рис. 5 показана таблица зависимостей параметра оптимизации от варьируемых факторов, задаваемых пользователем.
Рис.2 Блок-схема алгоритма оптимизации
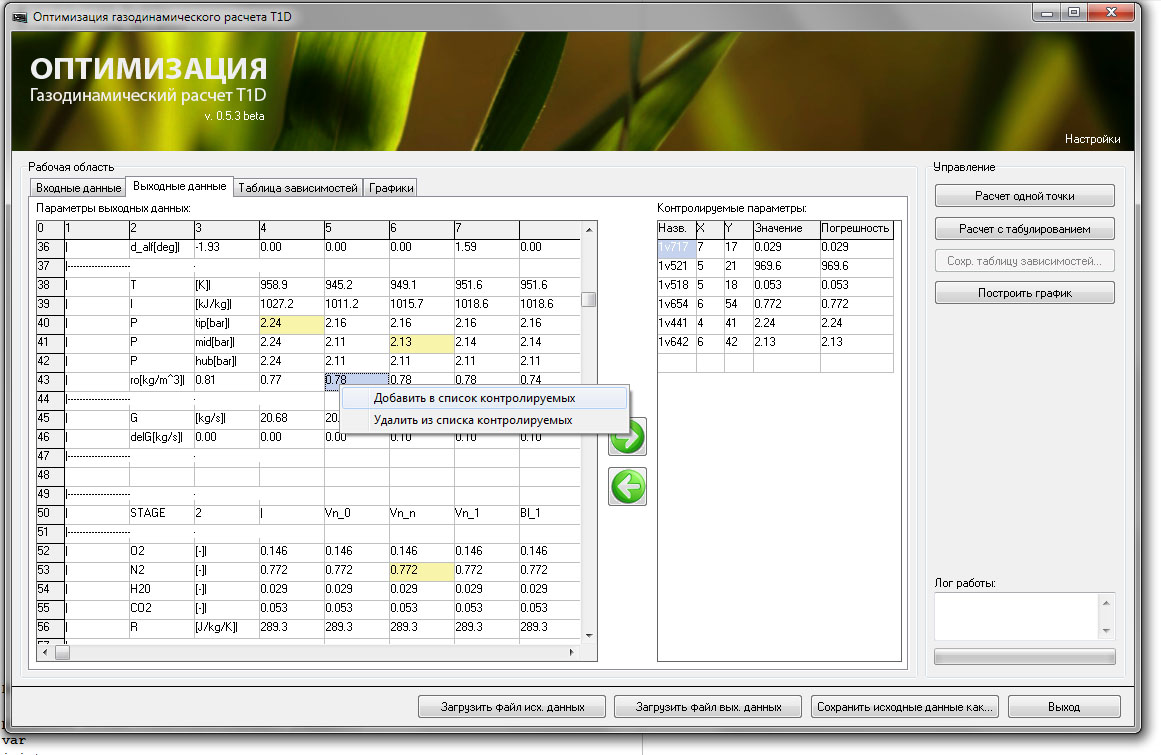
Рис. 3 Пример входных данных
Рис.4 Пример выходных данных
Рис. 5 Пример таблицы зависимостей табулируемых параметров
В основе работы программы заложена математическая модель оптимизации, основной задачей которой является сокращение количества запусков решателя. Это позволит значительно ускорить процесс оптимизации, сократить временные затраты на получение требуемого результата и снизить аппаратные требования к рабочей станции.
Фактор считается заданным, если указаны его название и область определения. В выбранной области определения он может иметь несколько значений, которые соответствуют числу его различных состояний. Выбранные для эксперимента количественные или качественные состояния фактора носят название уровней фактора.
Значения факторов, соответствующие определенным уровням их варьирования, выражают в кодированных величинах. Под интервалом варьирования фактора подразумевается разность между двумя его значениями, принятая за единицу при кодировании (т.е. шаг).
При этом следует учитывать, что чрезмерное увеличение величины интервалов варьирования нежелательно, т.к. это может привести к снижению эффективности поиска оптимума. А очень малый интервал варьирования уменьшает область эксперимента, что замедляет поиск оптимума.
Для решения задачи оптимизации предложено большое количество алгоритмов, базирующихся на различных принципах, но лишь немногие из них нашли широкое применение. Среди них нет еще ни одного алгоритма, полностью удовлетворяющего всем предъявляемым требованиям. По-прежнему остается актуальной задача разработки новых более эффективных алгоритмов с широкой областью применения.
Преимущества или недостатки того или иного алгоритма, определяющие его применимость, нельзя оценить однозначно. Сравнение всегда приходится вести по ряду показателей, но опыт работ показывает, что достаточно сложные задачи удается решать только одним из методов поиска, т.е. таким методом, при котором последовательно вычисляются значения функции цели и проверяются ограничения в различных точках области поиска. Различные алгоритмы этого типа, собственно говоря, и различаются способами выбора последовательности этих точек.
При оптимизации ГТД не встречаются задачи без ограничений. Они бывают, как правило, бывают нелинейными. Функция цели часто многоэкстремальная, поэтому преимущественно применяются методы глобального поиска, но возможно и применение локальных методов при достаточно большой области притяжения глобального экстремума. В этом случае приходится для повышения надежности повторять поиск из нескольких начальных точек.
Рассмотрим пример проведения неформальной оптимизации по двум
факторам с использованием разрабатываемого программного комплекса.
Т.е при табулировании Xi выявляем
функцию цели
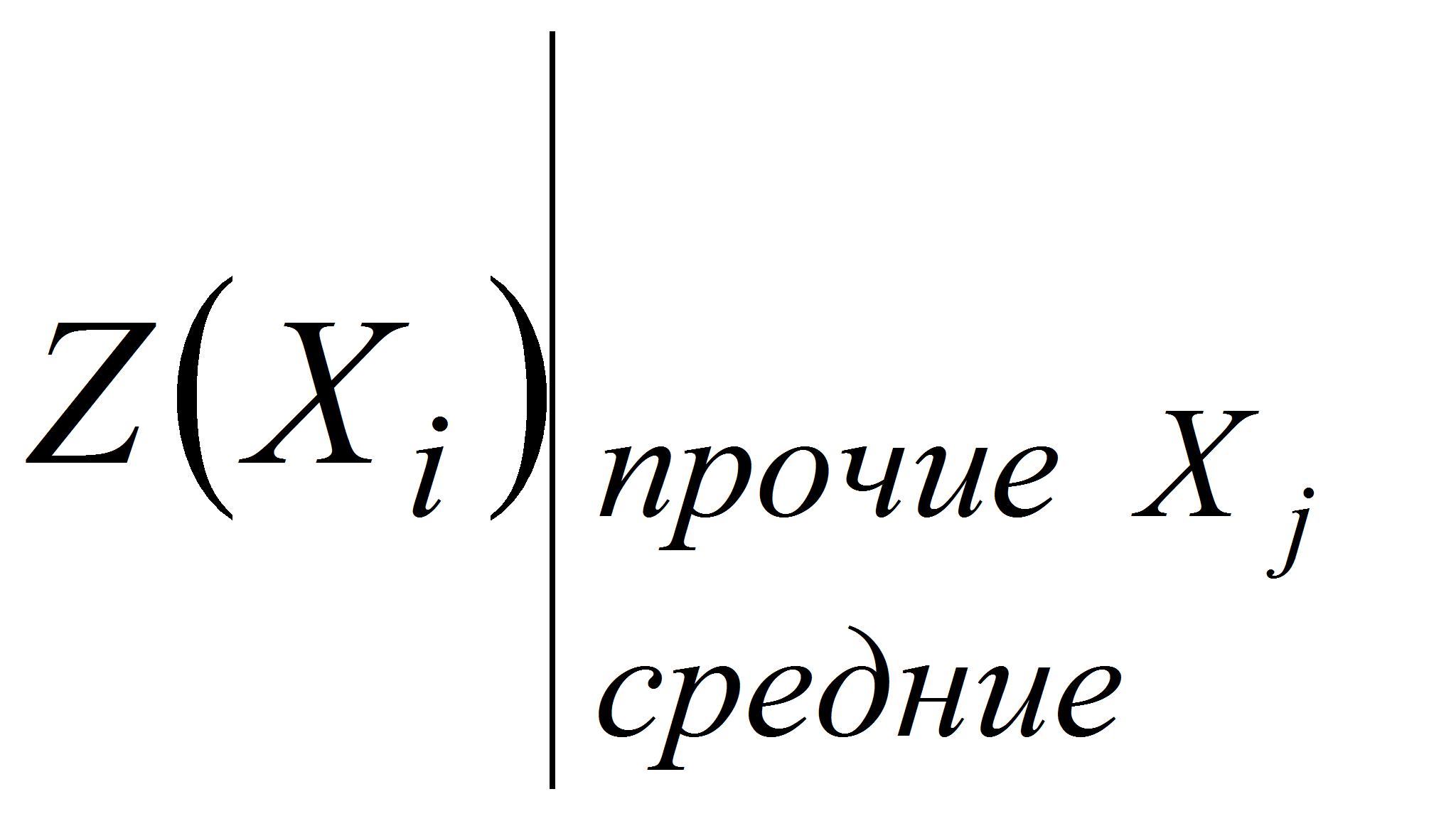 в
виде:
в
виде:
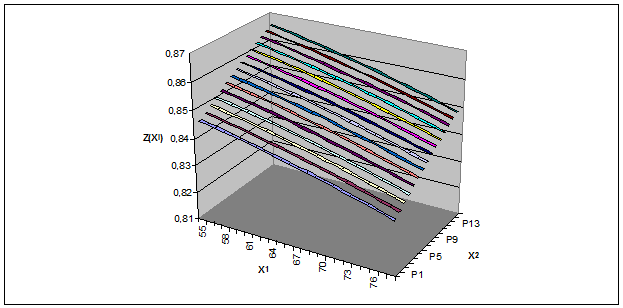
В результате имеем поверхность зависимости функции цели от воздействующих факторов (рис. 6).
Рис.6 Зависимость функции цели от воздействующих факторов
Далее по полученной поверхности зависимости функции цели от воздействующих факторов происходит поиск максимума функции цели с использованием методов поиска, описанных выше.
С ростом стоимости современного натурного и полунатурного эксперимента возрастает потребность в математическом моделировании рассматриваемых физических процессов. Одновременно с этим развивается и вычислительная техника, современный настольный компьютер на несколько порядков мощнее, чем ЭВМ на заре развития, когда они занимали целое крыло здания. А если обратить внимание на кластеры, состоящие из тысяч ядер, то это несравненно более мощный инструмент для расчетно-теоретических исследований. При такой эволюции вычислительной техники значительно совершенствовались и сами методы решения математических задач, и способы представления результатов. В настоящее время расчётно-теоретические исследования фактически становятся базой для экспериментов во многих областях науки и позволяют существенно снизить сроки и стоимость создания новой техники.
В промышленности зачастую возникают задачи, когда требуется использовать ранее созданные программы с уже созданным интерфейсом (в виде входных и выходных файлов), которые представляют собой так называемый «черный ящик» – эти программы имеют закрытые алгоритмы.
Рассмотрев существующие проблемы, возникающие при проведении расчетов на промышленных предприятиях нельзя не отметить актуальность разработки проекта программного оптимизационного комплекса.
Наличие такого комплекса позволит не только найти наиболее оптимальное решение поставленной задачи, но и значительно сократить временные затраты на совершенствование современных изделий. Позволит решать все классы оптимизации, включая уникальные задачи многопараметрической (100 и более переменных), многокритериальной (более 10 критериев) оптимизации, что позволит значительно повысить эффективность объекта оптимизации и получать технические решения и законы управления, не имеющие аналогов. Связать и решать в едином проекте задачи, рассчитываемые различными программными средствами на различных ПК, объединенных в локальную сеть или через Интернет (многодисциплинарная оптимизация). Определить наиболее эффективные технические решения по многим критериям, включая многоцелевое оптимальное управление (многокритериальная постановка). Минимизировать необходимое число определений целевой функции (число вычислений по математической модели либо проведения экспериментов) при поиске оптимального технического решения. Определить максимально достижимую эффективность системы.
Технология оптимизации первоначально используется при поиске путей повышения эффективности силовых установок и их узлов современных и перспективных летательных аппаратов различного назначения путем решения задач оптимального проектирования и оптимального управления. Но нет принципиальных сложностей в применении этой технологии, в экологии, биотехнике, экономике и т.п. при условии наличия соответствующих математических моделей и участия в проведении исследований специалистов из этих областей.
Работа выполнена при финансовой поддержке РФФИ (проект №10-08-00795)
Литература:
Тунаков А. П. САПР газотурбинных двигателей / А.П. Тунаков, И.А. Кривошеев, Д. А. Ахмедзянов – Уфа: УГАТУ, 2005. – 272 с.
Адлер Ю.П. Планирование эксперимента при поиске оптимальных условий./ Ю.П. Адлер, Е.В. Маркова, Ю.В. Грановский. Издательство Наука, Москва 1976, 279с.
Банди Б. Методы оптимизации. Вводный курс: Пер. с англ. М.: Радио и связь, 1988. — 128 с: ил.
Налимов В.В. Теория эксперимента. М.: Наука, 1971. - 208 с.