Проблема творчества и формирования креативных способностей занимает одно из центральных мест в философии, психологии и педагогике. Исследованием творческой деятельности занимались философы И. Кант, Платон, Ж. П. Сартр, М. Хайдеггер, Ф. Шеллинг, А. Т. Шумилин, психологи Ж. Адамар, Д. Б. Богоявленская, Л. С. Выготский, Дж. Гилфорд, В. Н. Дружинин, В. А. Крутецкий, Ю. Н. Кулюткин, А. М. Матюшкин, Я. А. Пономарев, В. Н. Пушкин, педагоги Р. Капентер, И. Я. Лернер, Г. И. Патяко, П. И. Пидкасистый, Г. И. Щукина и другие. Они рассматривали построение теоретической модели творческой деятельности, взаимосвязи творческой деятельности, сознания и личности, механизмы влияния этой деятельности на развитие творческих возможностей человека, психологическую структуру творческой деятельности, организацию и условия успешного протекания творческой деятельности учащихся.
Однако на практике внедрение технологий, способствующих формированию креативных (творческих в широком смысле*) способностей учащихся проблематично. Среди причин этого явления можно указать значительную разобщенность теоретических подходов и объективную сложность формирования творческой деятельности учащихся.
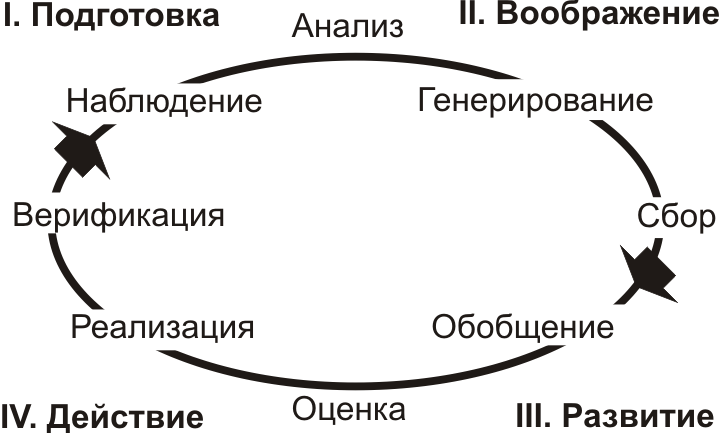
В рамках нашего исследования для формирования креативных способностей рассмотрим модель предложенную в статье The Cycle of Creativity and How to Ride It [1] ее автор Mary Jaksch приводит внутренние трудности, с которыми сталкивается человек на пути развития креативных способностей, акцентируя внимание на невыполнении или пропуске последовательных этапов, способствующих формированию креативности. Рассмотрим модель процесса проявления креативности по Paul E. Plsek: Working Paper: Models for the Creative Process (рис. 1) [2]. Автор выделяет четыре основных этапа:
|
Рис 1. Модель процесса проявления креативности |
Подготовка. Это этап наблюдения и восприятия окружающего мира. Чем богаче внутренне мы становимся, тем больше возможностей для творческой деятельности получаем.
Воображение. Когда происходит процесс интериоризации, мы начинаем анализировать информацию и систематизировать ее. На этом этапе важно осознавать стериотипизацию нашего восприятия и мышления. Генерирование идей происходит тогда, когда мы начинаем комбинировать, казалось бы, совсем несовместимые паттерны. Развитое воображение и способность визуализации помогают выйти за пределы собственного опыта и смоделировать новый образ (идеи, ситуации и т.д.).
Развитие. Из списка набросков идей выбираются наиболее удачные для дальнейшего развития и детальной проработки.
Действие. Завершающий этап проявления креативности который включает в себя реализацию и верификацию результата. Если верификация выявит недочеты, процесс запустится заново.
Эта модель согласует с базисом инновационного мышления, используемым для формирования креативного мышления учащихся. Базис инновационного мышления [4]: системность; логичность; диалектичность; воображение. Каждый из этих компонентов должен основываться на творческом потенциале мышления как способности человека к созданию инновации.
Системность. Любая инноватика есть или усовершенствование какой-либо существующей системы, или создание новой, ранее не существующей. В окружающем мире все взаимосвязано: любой объект одновременно и является элементом другой, более крупной системы, и сам есть целостная система со своими элементами.
Логичность. Использование аппарата традиционной логики незаменимо при решении простейших творческих «повседневных» задач.
Диалектичность. Создание нового не может быть основано на традиционной логике. Для его создания необходимо преодолеть препятствие – разрешить противоречие.
Воображение. Только человеческий мозг обладает таким свойством. История культуры в целом – это история человеческого воображения. Умение представлять несуществующие объекты, находить связи между самыми отдаленными, на первый взгляд, объектами – задача воображения.
Во второй половине XX века сформировалась как научное направление ТРИЗ (теория / технология решения изобретательских задач) Г. С. Альтшуллера [3]. Исторически, сутью ТРИЗ является целенаправленный поиск решения, совмещенный с отбором из предполагаемых вариантов наиболее сильных без сплошного перебора слабых. Области современного ТРИЗ весьма широки: в построении сюжетов литературных произведений, живописи, искусстве (Ю. Мурашковский, С. В. Козловский, О. Алешина и др.), в биологии (В. А. Бухвалов, И. Н. Самаль, В. И. Тимохов, И. Андржеевская и др.), в математике и методике математического развития (А. А. Страунинг, В. М. Цуриков, А. В. Козлов, Т. В. Погребная и др.), в физике (А. Гин и др.), в географии (Т. В. Иванова и др.), в педагогике и психологии (А. Н. Тубельский, Н. Н. Хоменко, И. С. Якиманская, С. Ю. Модестов, Ю. Г. Тамберг, М. Н. Шустерман, З. Г. Шустерман и др.), в теории опережающей педагогики (М. И. Меерович, Л. П. Шрагина), в бизнесе (В. Г. Сибиряков, С. В. Сычев, О. И. Сычева и др.), в рекламе (И. Л. Викентьев) и т.д. Ряд наработок позволяет применять инструменты ТРИЗ при обучении в общеобразовательной школе.
Можно с достаточной эффективностью использовать элементы ТРИЗ в учебном процессе для развития элементов инновационного мышления. Эффективность отдельных приемов убедительно была доказана в ходе экспериментальной работы по применению ТРИЗ в педагогике [5, 8, 9, 10, 11, 13].
Совокупность правил, определяющих построение новых конструктивных образов, называется алгоритмом. Обобщенные алгоритмы, на основе которых могут быть построены специализированные (ориентированные на определенное приложение, на определенный класс моделей) или детализированные (более точные) алгоритмы в ТРИЗ называются мета-алгоритмами [7].
Для примера рассмотрим применение мета-алгоритма ТРИЗ в преподавании математики. Хотя школьная математика отлична от математики – науки [6], но преемственность построения рассуждений сохраняется.
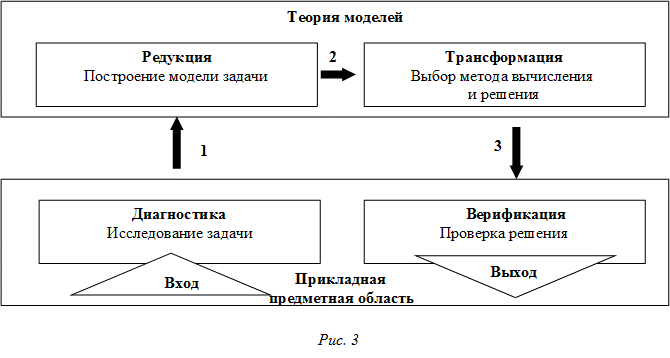
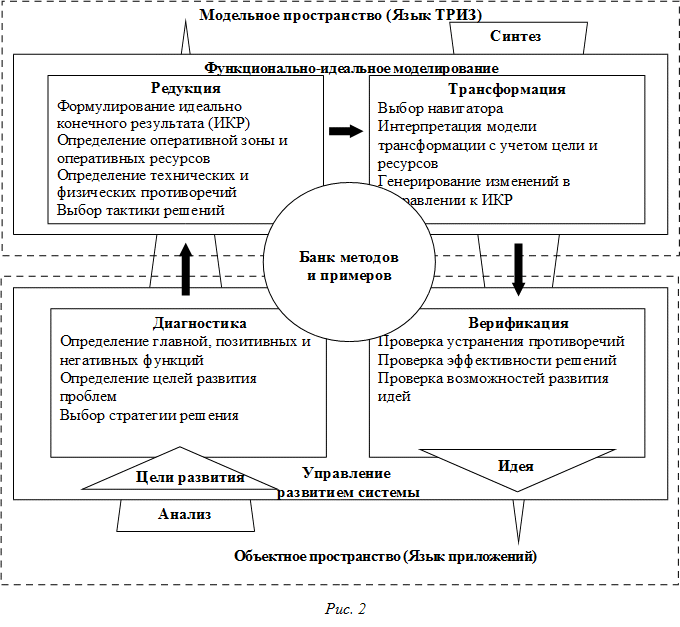
Рассмотрим обобщенную схему мета-алгоритма изобретения (рис. 2), а также упрощенный мета-алгоритм для решения некоторого класса учебных математических задач (рис. 3). Тогда ход решения задачи можно уложить в 4 крупных этапа: диагностика (исследование задачи), редукция (построение модели задачи: алгебраической, аналитической и др.), трансформация (выбор метода решения (вычисления) модели), верификация (проверка решения).
При этом данная схема совпадает с методикой организации решения учебной математической задачи соблюдением формально-логической схемы рассуждения «анализ – построение – доказательство – исследование» при решении геометрических задач на построение и т.п. [12]. Переходы 1 и 3 требуют знания теории моделей и прикладных областей ее применения. Переход 2 требует умения строить и решать модели теории.
Пример 1. В двух цехах завода стоят станки двух типов. Первого типа 2 и 1 соответственно в первом и втором цехе, второго – 6 и 2. Определите среднею мощность, потребляемой станком каждого типа, если первый цех потребляет 340 киловатт-часов, второй – 130.
Решение представим в виде мета-алгоритма (рис. 4). Пусть в двух цехах завода работает разное количество станков двух типов. Для точного определения средней мощности, потребляемой станком определенного типа, было решено воспользоваться имеющимися измерениями расхода электроэнергии по каждому цеху за сутки. На этапе диагностики проблемы было установлено количество станков каждого типа и данные по потреблению электроэнергии. На этапе редукции была построена система из двух линейных уравнений с двумя неизвестными. На этапе трансформации из двух простейших подходящих методов (метод исключения переменных и метод замены и подстановки переменных) выбрали последний. На этапе верификации путем прямой подстановки полученных значений искомых переменных в исходные уравнения убедились в правильности решения задачи.
Таким образом, при использовании мета-алгоритма появляется возможность более наглядно представлять ход решения математических задач.
На этапах диагностики и редукции преимущественно используется анализ проблемы решения, на этапах трансформации и верификации – синтез идеи решения. Тем самым, используя при решении задачи мета-алгоритм, у учащегося на уроках «подстегивается» не просто логическая составляющая мышления, а проявляется и системность (переходы 1, 2 и 3) и воображение (переход 1). Переход 2 всегда направлен на развитие систем с целью получения наибольшей пользы (при их функционировании). Но любое развитие всегда наталкивается на препятствия (противоречия). Очередной шаг в развитии будет достигнут только при преодолении этих препятствий (противоречий). Развитие идет через преодоление противоречий. А, значит, проявляется и диалектичность.
Используя на уроках математики мета-алгоритм ТРИЗ, ребенок осознано учиться использовать разные составляющие инновационного мышления (рис. 2) а так же логично реализует четыре основных этапа модели процесса проявления креативности (рис. 1).
Как показывает опыт, указанный адаптированный инструмент ТРИЗ и другие с одной стороны учат как надо действовать для того, чтобы получить желаемый продукт, результат, какие нормы надо соблюдать, чтобы получить продукт гарантированного качества и дают возможность интегрировать часть полученной учебной информацию на уроках с гуманитарными и естественными наукам в единую систему знаний, с другой методы результативно можно использовать для повышения уровня развития инновационного мышления на базе модели проявления креативности (рис. 1).
Примечания
* Творчество в широком смысле рассматривается как деятельность в ситуации неопределенности, направленная на получение результатов, обладающей объективной или субъективной новизной. В этом плане она не обязательно связана с такими видами деятельности, традиционно относимые к «творческим», как рисование, сочинение музыки и стихов, и т.п. Оно проявляется, когда приходиться действовать в ситуациях неопределенности, при отсутствии четких алгоритмов, неизвестности сути и способов решения, встающих перед человеком проблем.
Литература:
Jaksch Mary. The Cycle of Creativity and How to Ride It [Электронный ресурс] / Mary Jaksch //02 июня 2009г./ Режим доступа: http://writetodone.com/2009/06/02/how-to-ride-the-cycle-of-creativity/ . Дата обращения: 15.09.2010г.
Paul E. Plsek. Working Paper: Models for the Creative Process. [Электронный ресурс] / Paul E. Plsek // DirectedCreativity is a trademark of Paul E. Plsek & Associates, Inc / Режим доступа: http://www.directedcreativity.com/pages/WPModels.html. Дата обращения: 15.09.2010г.
Альтшуллер, Г.С. Найти идею. Введение в теорию решения изобретательских задач / Г.С. Альтшуллер. – 2-е изд., доп. – Новосибирск: Наука. Сиб. отд-ние, 1991. – 225 с.
Блейхер, О.В. Взаимодействие инновационных образовательных процессов как необходимое условие модернизации образования при становлении постиндустрильного общества [Электронный ресурс]/ О.В. Блейхер // Управление общественными и экономическими системами: сборник материалов научной конференции / Орловский государственный технический университет, 2006г. / Режим доступа: http://elibrary.ru/item.asp?id=9288713. Дата обращения: 10.09.2009
Модестов, С Ю. Проектирование образовательных технологий на основе ТРИЗ [Текст]: автореф. дис. канд. пед. наук: 13.00.01 / С. Ю. Модестов; СПб: РГПУ им. А.И. Герцена, 2001. – 18 с.
Мордкович А. Г. Беседы с учителями математики [Текст]: учеб.-метод. пособие / А. Г. Мордкович. – М.: Оникс 21 век, 2005. – 336 с.
Орлов М. А. Основы классической ТРИЗ. Практическое руководство для изобретательного мышления [Текст] / М. А. Орлов. – М.: СОЛОН-ПРЕСС, 2006. – 432 с.
Педагогика + ТРИЗ [Текст]: сборник статей для учителей, воспитателей и менеджеров образования. №1-6. – Мн.: ПолиБиг, 1997 – 2001г.
Терехова, Г.В. Творческие задания как средство развития креативных способностей школьников в учебном процессе [Текст]: автореф. дис. канд. пед. наук: 13.00.01 / Г. В. Терехова. – Челябинск, 2002.
Учителям о ТРИЗ. Выпуск 1 -5 [Текст]: сборник методических материалов по преподаванию ТРИЗ. – Спб.: Союз писателей Санкт Петербурга 1999-2006г.,.
Фёдорова, Е.А. Развитие творческой активности студентов средствами ТРИЗ-педагогики (на примере изучения информатики) : автореф. дис. на соиск. учен. степ. канд. пед. наук: 13.00.01: защищена 22.12.09 / Фёдорова Е.А.-Ульяновск:[б. и.],2009.-22 с.
Хинчин А. Я. О воспитательном эффекте уроков математики [Текст] / А. Я. Хинчин // Повышение эффективности обучения математике в школе. – М.: Просвещение, 1989. – С. 18-37.
Ширяева, В.А. Развитие системно-логического мышления учащихся в процессе изучения теории решения изобретательских задач (ТРИЗ) [Текст]: автореф. дис. канд. пед. наук / В. А. Ширяева. – Саратов: СГУ им. Н. Г. Чернышевского, 2000. – 18 с.