Особое место среди авиационных технических средств занимают многороторные плоские многоцелевые воздушные платформы – беспилотные летательные аппараты, предназначенные для размещения специальной наблюдательной аппаратуры (радаров, лидаров, фотоаппаратов, видеокамер) или перевозки мелких грузов на небольшие расстояния, в т.ч. со сбросом его в процессе полета. Интегрированный фюзеляж летательного аппарата позволит корпусу платформы создавать в полете дополнительную аэродинамическую подъемную силу. Скрытая в нем силовая установка защищена от повреждения при контакте летательного аппарата с элементами строительных и технологических конструкций, а также с препятствиями естественного происхождения.
Импеллер – это винт, заключенный в кольцевой обтекатель. Своим вращением винт создает поток воздуха, перпендикулярный плоскости вращения, что образует силу по его оси. Использование нескольких винтов повышает надежность, но при этом осложняет управление, а именно балансировку.
В связи с этим исследование аэродинамики подобных платформ является актуальной задачей, особенно в разрезе влияние земли на подъемную силу винтов и возможности засасывания посторонних предметов с подстилающей поверхности.
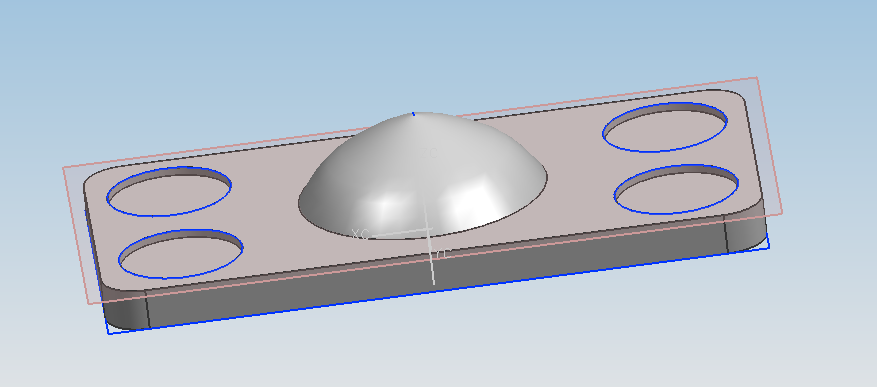
В данной задаче делается предположение, что поток на входе в импеллер равномерный, поэтому можно задать определенное значение скорости. На выходе из импеллера предполагается, что скорость имеет только вертикальную составляющую. Таким образом, предлагается заменить работу винта заданием значений скорости на входе и выходе из импеллера. Модель квадроимпеллерной платформы и расчетной области показана на рисунке 1. Осесимметричное тело на пластине – отсек для размещения полезной нагрузки.
Рисунок 1 – Модель квадроимпеллерной платформы
а – расчетная область; б – модель платформы
Расстояние от основания пластины до границы расчетной области вниз:
1) 200 мм – платформа у поверхности земли;
2) 800 мм – расстояние от поверхности земли до основания платформы равно длине платформы;
3) 3000 мм – платформа на значительном удалении от земли.
После подготовки 3D моделей в CFX-Mesh строится сетка.
Сеточные модели расчетной области представлены на рисунке 2.
Рисунок 2 – Сеточные модели расчетной области
В задачах, где платформа находится у поверхности земли на расстоянии 200, 800 и 3000 мм, на нижней границе ставится граничное условие стенка (Wall), а там, где исключается влияние нижней стенки ставится граничное условие открытая поверхность (Opening, избыточное давление 0 Па) (рисунок 3). На остальных поверхностях граничное условие Opening (избыточное давление 0 Па).
Рисунок 3 – Подготовленные к расчету модели платформы
Параметры расчетной области:
воздух подчиняется закону идеального газа;
опорное давление 101325 Па;
модель теплопереноса – изотермическая;
модель жидкости – несжимаемая;
модель турбулентности – стандартная k-e;
температура в расчетной области – 288 К.
Воздух входит в верхнюю часть импеллера и выходит из нижней, в CFX-Pre верхняя часть названа Выходом (Outlet), потому что для данной задачи воздух выходит из расчетной области, а выходная часть названа Входом (Inlet) воздух входит в расчетную область. При этом на Выходе и Входе заданы значения скорости, скорость на Входе увеличивается за счет работы винта.
Граничное условие Outlet: нормальная скорость 40 м/с.
Граничное условие Inlet: нормальная скорость 100 м/с.
Подготовленные к расчету четыре модели экспортируются в CFX-Solver, критерием остановки расчета является сходимость по параметрам потока 10-4.
Анализ результатов расчета
В результате расчета получены поля скоростей и других параметров во всей расчетной области.
1) Граничное условие Opening по всем поверхностям параллелепипеда.
На рисунке 4 показано распределение скоростей вблизи платформы.
Рисунок 4 – Распределение скоростей вблизи платформы
2) Граничное условие Wall у поверхности земли, на остальных поверхностях параллелепипеда граничное условие Opening. Расстояние до поверхности земли 0,2 м.
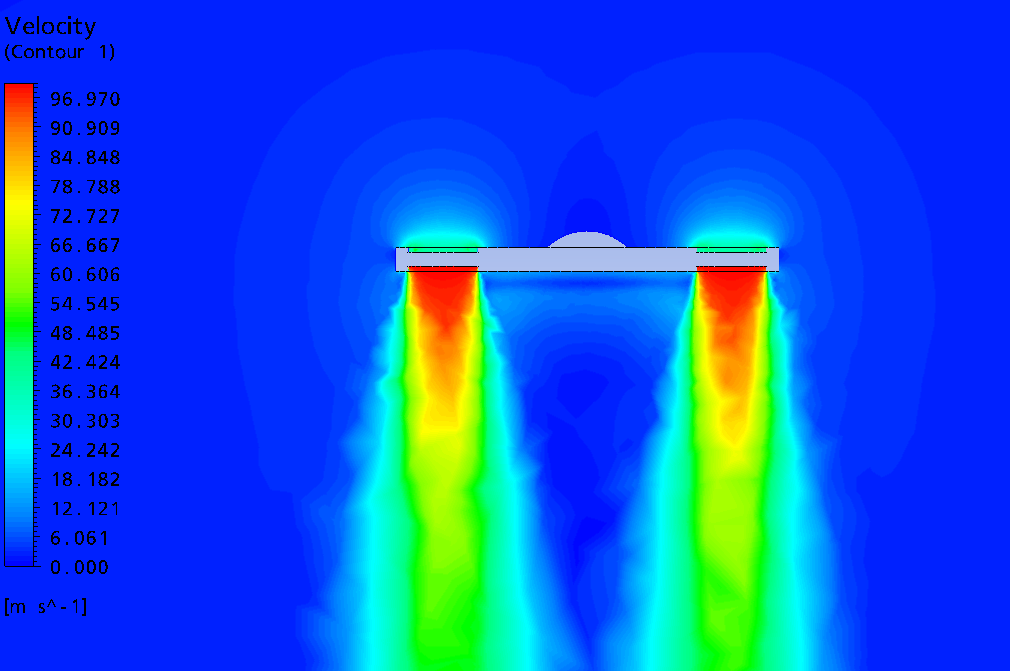
На рисунке 5 показано, как поток соударяется с землей и растекается.
а
б
Рисунок 5 – Распределение скоростей в случае соударения потока с землей
а – линии тока, распространяющиеся от выхода; б – векторное поле скоростей
Сила действующая на отдельные участки платформы (вертикальная составляющая):
fwall = 4,10 Н; finlet = 836,77 Н; foutlet = -43,16 Н.
Суммарная сила F = fwall + finlet + foutlet = -4,10+836,77-43,16 = 797,71 Н.
3) Граничное условие Wall у поверхности земли, на остальных поверхностях параллелепипеда граничное условие Opening. Расстояние до поверхности земли 0,8 м.
Сила действующая на отдельные участки платформы (вертикальная составляющая):
fwall = -3,03 Н; finlet = 822,08 Н; foutlet = -36,08 Н.
Суммарная сила F = fwall + finlet + foutlet = -3,03+822,08-36,08 = 782,97 Н.
4) Граничное условие Wall у поверхности земли, на остальных поверхностях параллелепипеда граничное условие Opening. Расстояние до поверхности земли 3,0 м.
Сила действующая на отдельные участки платформы (вертикальная составляющая):
fwall = -32,03 Н; finlet = 822,56 Н; foutlet = -41,56 Н.
Суммарная сила F = fwall + finlet + foutlet = -38,96+821,77-41,40 = 748,97 Н.
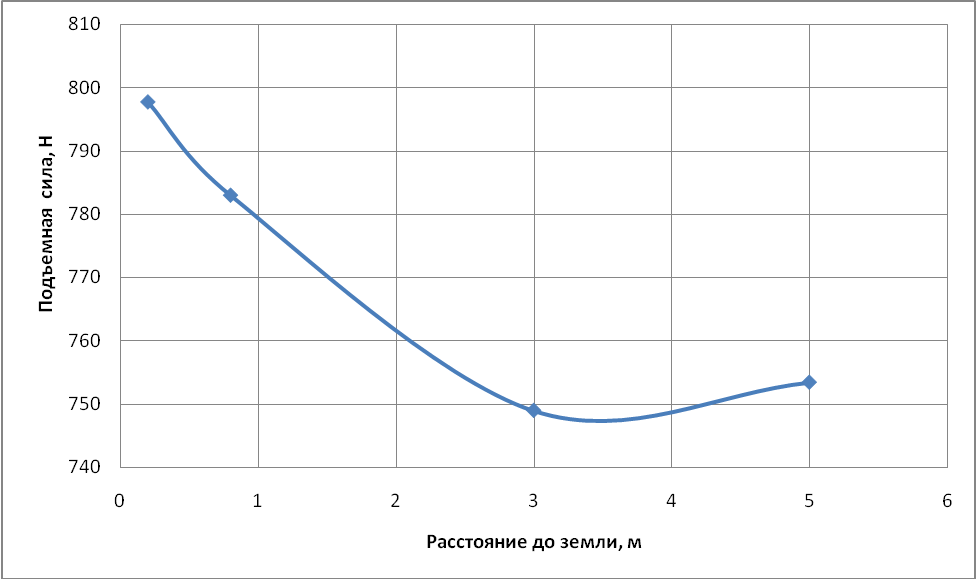
По результатам расчета в ANSYS CFX можем построить зависимость подъемной силы от расстояния до земли (таблица 1). Когда на всех поверхностях параллелепипеда задано граничное условие Opening, это эквивалентно удалению платформы от земли на бесконечно большое расстояние, где влияние земли исключается. На рисунке 6 построен график по данным таблицы 1.
Таблица 1 – Зависимость подъемной силы от высоты
|
Расстояние до земли |
Подъемная сила, Н |
|
0,2 м |
797,71 |
|
0,8 м |
782,97 |
|
3,0 м |
748,97 |
|
бесконечность |
753,42 |
Рисунок 6 – Зависимость подъемной силы от расстояния до земли
Заключение
По данным таблицы 1 можно сделать вывод, что суммарная подъемная сила уменьшается с увеличением расстояния от платформы до поверхности земли, что соответствует действительности.
Подъемная сила складывается из силы, действующей на винт и подъемной силы воздуха, действующей на платформу.
При небольшом расстоянии от поверхности земли до основания платформы воздух, выходящий из винтов ударяется о землю и изменяет свое направление. Создается обратное течение и статическое давление под платформой повышается, получается подобие экранного эффекта. С увеличением расстояния до поверхности земли экранный эффект пропадает.
При большом удалении платформы от поверхности земли статическое давление на нижней поверхности платформы ниже, чем на верхней. Поток, выходящий из винтов создает разрежение и статическое давление падает.
Для данной задачи удаление платформы от земли на 3 м эквивалентно удалению платформы на бесконечность (влияние земли пропадает), подъемные силы приближенно равны.
Из рисунка 6 видно, что расчет при расстоянии до земли 3 м выпадает из ряда. Физически, значения подъемных сил в последних двух точках (рисунок 6) приближенно должны быть равны, но из-за недостаточного качества сетки появляется неточность результатов. Поэтому, проводя расчеты при больших расстояниях до земли мы получим не постоянные значения, а колебание значений подъемной силы около некоторого среднего значения.