В настоящее время уровень развития науки и техники предъявляет к будущим специалистам, использующим в своей профессиональной деятельности математику, высокие требования к знаниям, умениям и навыкам как математического, так и прикладного характера. Начиная с 60-х годов, параллельно идее политехнизации обучения обозначился процесс, связанный с порождением так называемой «прикладной направленности» в преподавании математики. Это было вызвано широкой математизацией большинства современных наук и привело в движение процессы, связанные с внедрением в школьную математику задач не только производственного содержания, но и задач из области экономики, социологии и других сфер человеческой деятельности. Методическая наука имеет в своем активе значительное число исследований, связанных с проблемой обучения школьников применениям математики.
Дополнительное математическое образование школьников должно ставить перед собой задачи повышения прикладной значимости предмета, а значит, повышения общего уровня развития учащегося, подготовки школьника к дальнейшему образованию и самообразованию и к творческой деятельности по любой специальности. Математическое образование само по себе является наиболее важной составляющей того, что дает школа. А добавление в школьный курс прикладной направленности математики и использование компетентностного подхода позволяет показать учащимся всю важность этой учебной дисциплины. Дополнительное математическое образование школьников взаимосвязано с их внеклассной работой и входит в состав непрерывного математического образования.
Объяснение учащимся прикладной направленности математики, показ широчайшей области применения этих знаний – побуждает у обучаемых потребность в знаниях и вызывает интерес к предмету, соответствует развитию способностей каждого учащегося, учит применять полученные знания на практике и самостоятельно приобретать их. Также целесообразно в обучении математике следовать основным дидактическим принципам обучения: от простого к сложному, от конкретных наблюдений, примеров и опытов к выводам и обобщениям, от практических результатов к формулировкам правил и теорем.
Успехи в обучении математике во многом зависят от развития у учащихся устойчивого интереса к предмету. Прежде всего, следует помнить, что интерес к математике вырабатывается тогда, когда школьнику понятно, о чем говорит учитель, когда предлагаемые ему задачи интересны по содержанию или методам решения, когда школьнику предоставляется возможность самому подумать, самому сделать вывод, обобщение и т. д. То есть когда преподаватель использует компетентностный подход.
Эффективному обучению также во многом способствует решение задач с практическим содержанием, что определяет развитие у учеников компетентности. После получения порции новых знаний дети нуждаются в их практическом подтверждении. Иначе у них пропадает желание учиться. «Зачем нам это нужно?» - постоянно спрашивают они. И учителю приходится оправдывать государственные стандарты образовательных программ, показывая значимость преподаваемого материала. А если по какой-то причине преподаватель не может ответить на поставленный вопрос, у учеников возникают мысли «вот, даже учитель не знает, зачем это нужно, значит можно не учить». И, конечно же, он будет не прав, но поймет это только в будущем, когда будет уже слишком поздно. Поэтому необходимо не только вводить прикладную направленность математики, добиваясь внедрения и использования компетентностного подхода на уроках, но и создавать новый школьный предмет «прикладная математика». Это в какой-то мере развяжет руки преподавателям, и они смогут на практике показывать важность своего предмета ученикам. А это, в свою очередь, поднимет общую успеваемость учеников, потому что, как только что отмечалось, для школьников важно знать, для чего их учат и как это может пригодиться им в будущем.
К целям внедрения компетентностного подхода при преподавании математики можно отнести формирование:
· умений применять полученные знания для решения простейших задач жизненной практики, в изучении других учебных предметов (физики, химии, черчения и т.д.)
· умений пользоваться математическими инструментами и приборами
· умения самостоятельно добывать знания (работа с учебной и научно-популярной литературой).
· понимания необходимости изучения математических дисциплин.
Тем не менее, следует отметить, что в работах, посвященных рассмотрению вопросов экономики на занятиях по математике, уделяется недостаточно внимания возможностям компьютерных технологий обучения при решении задач с экономическим содержанием учащимися старших классов средней общеобразовательной школы. Использовать компетентностный подход необходимо также с внедрением персональных компьютеров, это позволит сделать уроки более интересными и наглядными, повысит качество и эффективность обучения. Благодаря возможностям компьютера можно наглядно демонстрировать области применения математики на практике не только с помощью учебных программ, но и показывая обучающие видеофильмы. Также при решении задач, например, с экономическим содержанием, необходимо учитывать в различные сроки большое количество переменных и зависимостей между ними, изменение и уточнение исходных описаний, что приводит к необходимости использовать компьютер в учебном процессе. Поэтому информатизация школ – процесс хоть и дорогой для государства, но крайне необходимый.
Таким образом, введение в школьную программу преподавания математики с использованием компетентностного подхода необходимо для реализации наметившейся государственной программы по подготовке экономически грамотного молодого поколения.
Разделение учащихся по сходству уровней развития специальных способностей требует учитывать его при формировании содержания обучения, направленного на развитие этих способностей. Анализ работ разных авторов позволяет выделить свойства содержания учебного материала, положительно влияющие на развитие специальных способностей. Так, развитию математических способностей школьников содействуют такие особенности содержания учебного материала как: абстрактность, обобщенность, формализованность, логичность, наличие взаимно обратных утверждений. Для формирования экономического стиля мышления важно, чтобы содержание учебного материала было четко структурировано и систематизировано, включало различные подходы к решению проблем. Для развития способностей естественно–научного мышления имеют значение исследовательский характер заданий, индуктивный метод изложения, привлечение естественной наглядности. Развитию гуманитарных способностей отвечает содержание, излагаемое естественным языком и наполненное иллюстрациями, личностными отношениями, удовлетворяющее требованиям эстетики.
Покажем на примере, как изменится содержание математического учебного материала с привнесением в него элементов, отражающих высокий уровень развития определенных специальных умственных способностей учащихся. Так, при знакомстве с определением поворота плоскости школьникам могут быть предложены для запоминания его различные формулировки. Предполагается, что направление поворота учтено в знаке градусной меры угла. В частности, определение может быть предложено учащимся с математическим складом ума в наиболее формализованном виде, с максимально возможным для школьного курса использованием математической символики. Например, можно представить его в таком виде: «Поворотом плоскости вокруг точкиО на угол a (обозначается 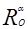 ) называется отображение плоскости на себя, при котором каждая точка М отображается в такую точку М1 (
) называется отображение плоскости на себя, при котором каждая точка М отображается в такую точку М1 (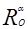 (М) = М1), что ОМ = ОМ1, ÐМОМ1 = a. При этом
(М) = М1), что ОМ = ОМ1, ÐМОМ1 = a. При этом 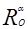 (О) = О». Для будущих экономистов это определение может быть более четко структурировано разбиением на отдельные признаки. Оно может выглядеть так: «Поворот плоскости вокруг точки О на угол a – это 1) отображение плоскости на себя, при котором каждая точка М отображается в такую точку М1, что: 2) ОМ = ОМ1; 3) угол МОМ1 равен a; 4) точка О отображается сама на себя». Для учащихся с естественнонаучным стилем мышления может быть предложено генетическое определение: «Пусть на плоскости задана некоторая точка О. Каждую точку М плоскости можно отобразить на точку М1 плоскости следующим образом. Надо провести луч ОМ, отложить от него заданный угол a, на второй стороне угла отложить отрезок ОМ1, равный отрезку ОМ. При этом точка О отобразится сама на себя. Такое отображение плоскости на себя называется поворотом вокруг точки О на угол a». «Гуманитариям» можно предложить менее формализованное генетическое определение: «Предположим, что на плоскости отмечена некоторая точка О. Каждую точку М плоскости можно отобразить на другую точку М1 плоскости следующим образом. Надо провести луч ОМ, отложить от него заданный угол, на второй стороне угла отложить отрезок ОМ1, равный отрезку ОМ. Точку О надо отобразить саму на себя. Такое отображение плоскости на себя назовем поворотом вокруг точки О на заданный угол». Выбор учащимся для запоминания той или иной формулировки может быть показательным в выявлении преобладающего стиля мышления.
(О) = О». Для будущих экономистов это определение может быть более четко структурировано разбиением на отдельные признаки. Оно может выглядеть так: «Поворот плоскости вокруг точки О на угол a – это 1) отображение плоскости на себя, при котором каждая точка М отображается в такую точку М1, что: 2) ОМ = ОМ1; 3) угол МОМ1 равен a; 4) точка О отображается сама на себя». Для учащихся с естественнонаучным стилем мышления может быть предложено генетическое определение: «Пусть на плоскости задана некоторая точка О. Каждую точку М плоскости можно отобразить на точку М1 плоскости следующим образом. Надо провести луч ОМ, отложить от него заданный угол a, на второй стороне угла отложить отрезок ОМ1, равный отрезку ОМ. При этом точка О отобразится сама на себя. Такое отображение плоскости на себя называется поворотом вокруг точки О на угол a». «Гуманитариям» можно предложить менее формализованное генетическое определение: «Предположим, что на плоскости отмечена некоторая точка О. Каждую точку М плоскости можно отобразить на другую точку М1 плоскости следующим образом. Надо провести луч ОМ, отложить от него заданный угол, на второй стороне угла отложить отрезок ОМ1, равный отрезку ОМ. Точку О надо отобразить саму на себя. Такое отображение плоскости на себя назовем поворотом вокруг точки О на заданный угол». Выбор учащимся для запоминания той или иной формулировки может быть показательным в выявлении преобладающего стиля мышления.
Дополнительное математическое образование школьников, включающее в себя компетентностный подход, – это образовательный процесс, имеющий свои педагогические технологии, формы и средства их реализации, по программам, дополняющим государственный стандарт.
К современному дополнительному математическому образованию школьников, использующему компетентностный подход, можно отнести:
- заочные школы при конкретных вузах или центрах непрерывного математического образования одаренных школьников, сами центры дополнительного образования;
- очно-заочные школы и летние физико-математические школы для одаренных детей;
- центры дополнительного математического образования одаренных школьников;
- учреждения дополнительного образования;
- системы спецкурсов (факультативы) для школьников, читаемых вузовскими преподавателями по отдельным разделам математики (экономико-математическое моделирование, финансовая математика, теория вероятности, линейное программирование, нестандартные задачи по элементарной математике и т.д.);
- олимпиады;
- школьные математические кружки;
- подготовительные курсы.
Дополнительное математическое образование, использующее компетентностный подход, дает возможность реализации отношений между педагогом и школьником, оптимального решения проблемы индивидуализации и дифференциации обучения как средства эффективного развития личности ребенка, построения профориентационной работы с учетом индивидуальных интересов, технологий обучения, как в общеобразовательной школе, так и в дополнительном математическом образовании.
Стремление же самого ученика, а впоследствии специалиста, к достижению профессиональной компетентности, имеет результатом то, что обеспечивается переход в процессе образования к самообразованию и повышению квалификации специалиста в дальнейшем на протяжении всего трудового и жизненного пути, а значит, это спасает специалиста от быстрого старения его профессиональной подготовки; общеобразовательную и профессиональную подготовку учащихся с учетом их интересов, способностей, мотивов и потребностей в современных рыночных условиях. Все это вместе взятое обеспечивает более высокую социальную защищенность специалиста на рынке труда.
Таким образом, реализация принципа компетентностного подхода в преподавании математики влечет за собой выполнение очень важных функций успешного разностороннего развития учеников и тем самым обеспечивает эффективную профессиональную подготовку выпускников.
Цель реализации компетентностного подхода в преподавании состоит в том, чтобы в результате его эффективного осуществления учащийся смог в своей практической деятельности выбрать и использовать из всей суммы знаний, умений, навыков, приобретенных им при изучении общеобразовательных и специальных предметов, те, которые необходимы ему для решения встающих перед ним практических задач.







