В последнее десятилетие машинное обучение стало набирать все большую и большую популярность и сегодня занимает одну из лидирующих позиций в сфере информационных технологий. Объем цифровых данных, используемый нами в повседневной жизни, увеличивается с каждым днем, в связи с этим, возникла необходимость в автоматическом анализе смарт-данных для дальнейшего развития технологического прогресса.
Сегодня машинное обучение активно используется для распознавания речи и образов, а также на его основе построены многие поисковые системы. Машинное обучение настолько прочно вошло в нашу повседневную жизнь, что ежедневное использование его методов остается для нас, как правило, незамеченным.
Активное развитие машинного обучения привело к распространению искусственных нейронных сетей [7]. Нейронные сети, основанные на биологической структуре человеческого мозга, превышают по своей вычислительной возможности прочие алгоритмы машинного обучения.
Одной из самых ярких и значительных форм искусственных нейронных сетей является сверточная нейронная сеть (СНС). Сверточная нейронная сеть была впервые предложена Я. Лекуном и Й. Бенгуа [1].
СНС состоит из трех основных видов слоев: сверточный слой, субдискретизирующий слой и выходной слой (чаще всего полносвязный) [2]. Слои СНС расположены друг за другом: сначала сверточный слой, а затем субдискретизирующий, за последним сверточным слоем следует выходной слой. Сверточный и субдискретизирующий слои считаются слоями двумерной размерности, а выходной слой, как правило, представляет собой вектор из пространства ![]() В СНС каждый двумерный слой имеет несколько уровней. Каждый уровень представляет собой двумерный массив. Выход каждого уровня в дальнейшем будем называть картой признаков. [6]
В СНС каждый двумерный слой имеет несколько уровней. Каждый уровень представляет собой двумерный массив. Выход каждого уровня в дальнейшем будем называть картой признаков. [6]
Математическая модель сверточной нейронной сети.
Для описания математической модели рассматриваемой нейронной сети будем использовать следующие обозначения.
Под ![]() будем понимать рассматриваемый в данный момент слой нейронной сети, где
будем понимать рассматриваемый в данный момент слой нейронной сети, где ![]() количество слоев в сети. За
количество слоев в сети. За ![]() обозначим количество карт признаков на слое
обозначим количество карт признаков на слое ![]() , а за
, а за ![]()
![]() функцию активации рассматриваемого слоя
функцию активации рассматриваемого слоя ![]() . Также, под переменной
. Также, под переменной ![]() будем понимать
будем понимать ![]() -ую карту признаков на слое
-ую карту признаков на слое ![]() [4].
[4].
Математическая модель сверточного слоя.
Введем в рассмотрение сверточный слой
− ![]() свертка, применяемая к карте признаков
свертка, применяемая к карте признаков ![]() слоя
слоя ![]() ), на слое
), на слое ![]() с картой признаков
с картой признаков ![]() ;
;
− ![]() пороговые значения, присоединяемые к карте признаков
пороговые значения, присоединяемые к карте признаков ![]() на слое
на слое ![]() ;
;
− ![]() список всех уровней слоя
список всех уровней слоя ![]() , которые соединяются с картой признаков
, которые соединяются с картой признаков ![]() слоя
слоя ![]() .
.
Таким образом, карта признаков ![]() сверточного слоя
сверточного слоя ![]() будет вычисляться следующим образом:
будет вычисляться следующим образом:
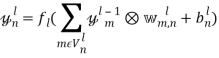 ,
,
где под оператором ![]() понимается математическая операция двумерной свертки.
понимается математическая операция двумерной свертки.
Предположим, что размер входных карт признаков ![]() равен
равен ![]() , а размер применяемой к ним свертки
, а размер применяемой к ним свертки ![]() равняется
равняется ![]() , тогда размер выходной карты признаков
, тогда размер выходной карты признаков ![]() вычисляется как:
вычисляется как:
![]() .
.
Математическая модель субдискретизирующего слоя.
Введем в рассмотрение субдискретизирующий слой ![]() . В сверточной нейронной сети
. В сверточной нейронной сети ![]() принято принимать четным числом, то есть
принято принимать четным числом, то есть ![]() . Для карты признаков
. Для карты признаков ![]() введем следующие обозначения:
введем следующие обозначения: ![]() фильтр, применяемый к
фильтр, применяемый к ![]() на слое
на слое ![]() , и
, и ![]() добавочное пороговое значение.
добавочное пороговое значение.
Далее будем действовать следующим образом: разделим карту признаков
![]()
Карта признаков ![]() субдискретизирующего слоя
субдискретизирующего слоя ![]() вычисляется, как:
вычисляется, как:
![]() .
.
Благодаря представленным выше рассуждениям, становится возможным посчитать размер ![]() карты признаков
карты признаков ![]() субдискретизирующего слоя
субдискретизирующего слоя ![]() :
:
![]() .
.
Математическая модель выходного слоя.
В данном параграфе будем рассматривать выходной слой ![]() , состоящий из единичных нейронов. Примем за
, состоящий из единичных нейронов. Примем за ![]() количество нейронов на данном слое. Как и при рассмотрении предыдущих слоев, обозначим за
количество нейронов на данном слое. Как и при рассмотрении предыдущих слоев, обозначим за ![]() фильтр, применяемый к карте признаков
фильтр, применяемый к карте признаков ![]() последнего сверточного слоя для получения перехода к нейрону
последнего сверточного слоя для получения перехода к нейрону ![]() выходного слоя. Пусть
выходного слоя. Пусть ![]() пороговое значение, добавляемое к нейрону
пороговое значение, добавляемое к нейрону ![]() .
.
Пользуясь введенными обозначениями, получаем формулу для подсчета значения выходного нейрона ![]() :
:
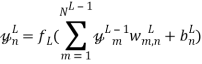 .
.
Таким образом, выходом сверточной нейронной сети является вектор следующего вида:
Математическая постановка задачи.
Таким образом, цель данной работы – минимизировать функцию потерь ![]() за счет выбора настраиваемых параметров обучаемой системы
за счет выбора настраиваемых параметров обучаемой системы ![]() .
. ![]() представляет собой арифметическое среднее функций вида:
представляет собой арифметическое среднее функций вида: ![]() , где
, где ![]() –
– ![]() -ый вход системы,
-ый вход системы, ![]() – несоответствие между желаемым выходом системы для
– несоответствие между желаемым выходом системы для ![]() и значением, которое выдает система.
и значением, которое выдает система. ![]() будем вычислять над обучающим множеством пар вида:
будем вычислять над обучающим множеством пар вида: ![]() .
.
Проведение эксперимента.
Описание базы данных.
Для тестирования разработанной системы была использована база данных, содержащая различные начертания английских букв: ![]() , и соответствующие им метки. Для обучения сети было использовано 24206 изображений, из которых 15106 изображений использовалось в качестве обучающей выборки и 9100 изображений в качестве тестовой. Размер каждого изображения составляет
, и соответствующие им метки. Для обучения сети было использовано 24206 изображений, из которых 15106 изображений использовалось в качестве обучающей выборки и 9100 изображений в качестве тестовой. Размер каждого изображения составляет ![]() пикселя. Каждый пиксель кодируется числом в интервале
пикселя. Каждый пиксель кодируется числом в интервале ![]() , где 0 соответствует черному цвету, а 1 – белому (рис. 1).
, где 0 соответствует черному цвету, а 1 – белому (рис. 1).
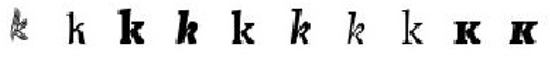
Рис. 1. Пример 10 изображений обучающей выборки для буквы k
Предварительная обработка изображений.
Предварительная обработка изображений необходима для достижения максимальной точности распознавания системы. Таким образом, полученная нейронная сеть будет инвариантна к незначительным искажениям: шуму, повороту и масштабированию.
Простые искажения изображения, такие как сдвиг, поворот и угловое смещение могут быть устранены путем применения простых аффинных преобразований. Также, для улучшения качества работы нейронной сети подаваемые на вход изображения дополнительно усреднялись.
Данный подход позволил получить сеть, обучение которой осуществлялось с применением различного набора изображений на каждой эпохе.
Описание архитектуры реализованной нейронной сети.
В работе была реализована и использована модель сверточной нейронной сети, содержащая 7 слоев. Обучение сети производилось в течение 150 эпох.
Первый слой использованной нейронной сети – сверточный. Ему на вход подается изображение размером ![]() пикселя, к которому применяется свертка размером
пикселя, к которому применяется свертка размером ![]() . Количество использованных фильтров – 20 (рис. 2).
. Количество использованных фильтров – 20 (рис. 2).

Рис. 2. Фильтры первого слоя сети, настроенные на распознавание простейших признаков
Размер выходных карт признаков данного слоя составляет ![]() пикселей.
пикселей.
Второй слой реализованной сети – слой субдискретизации. Основной функцией данного слоя являлось уменьшение размерности входного изображения и выбор пикселя с максимальным значением среди нескольких соседних. В данной архитектуре сети такой выбор осуществлялся между 4 соседними пикселями (рис. 3).

Рис. 3. Применение субдискретизации к одному изображению обучающей выборки
Третьим слоем рассматриваемой нейронной сети являлся сверточный слой, принимающий на вход 20 карт признаков предыдущего слоя. На данном этапе в качестве фильтров выбирались матрицы размера ![]() , формируя на выходе 50 карт признаков размером
, формируя на выходе 50 карт признаков размером ![]() пикселей.
пикселей.
Четвертый слой, как и второй слой нейронной сети, являлся слоем субдискретизации. Выходом данного слоя послужили 50 карт признаков –
Пятый слой реализованной нейронной сети – сверточный слой. На вход данному слою подавалось 50 карт признаков предыдущего слоя, к которым применялись фильтры размера ![]() . Таким образом, выход данного слоя представляет собой 500 карт признаков размером
. Таким образом, выход данного слоя представляет собой 500 карт признаков размером ![]() пикселя.
пикселя.
Задачей шестого слоя было применение нелинейной функции вида [7]:
![]() .
.
Использование данной функции наиболее удобно при обучении сверточной нейронной сети в силу простоты вычисления ее градиента (9), что значительно уменьшает время обучения сети, увеличивая при этом нелинейность выхода.
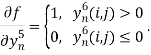 (9)
(9)
Седьмой слой рассматриваемой нейронной сети – полносвязный слой, содержащий 26 нейронов. Основной задачей данного слоя являлась классификация. В качестве функции активации данного слоя выбиралась softmax-функция вида [3]:
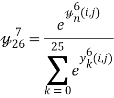 ,
,
а для сравнения получившихся значений функция:
![]() ,
,
где ![]() – желаемый выход для конкретного обучающего примера.
– желаемый выход для конкретного обучающего примера.
Примеры работы реализованной сверточной нейронной сети представлены на рисунках 4, 5, 6.

Рис. 4. Пример работы нейронной сети для произвольных букв (верхние буквы – исходные изображения, нижние – результат работы сети)

Рис. 5. Пример работы нейронной сети для одной буквы с добавлением различного шума: мультипликативный шум (I), гауссовский шум (II), шум типа «соль и перец» (III) (верхние буквы – исходные изображения, нижние – результат работы сети)

Рис. 6. Пример работы нейронной сети для одной буквы с искажениями (верхние буквы – исходные изображения, нижние – результат работы сети)
Сегментация текста на изображении.
Для использования полученной нейронной сети для распознавания подаваемых на вход слов и предложений с изображения необходимо осуществить предварительную сегментацию.
Основной идей использованного алгоритма являлось нахождение всевозможных способов разделения букв на изображении, а затем использование полученной нейронной сети для отыскания наиболее правильного разреза [5].
В первую очередь было сгенерировано множество всевозможных разрезов, к ним относились столбцы вертикальных пикселей изображения, сумма которых была наименьшей. При использовании данного подхода будем делать предположение, что необходимый нам разрез находится в рассматриваемом множестве.
Затем строился направленный ациклический граф описанным далее способом. Каждая вершина графа соответствовала одному из полученных ранее разрезов, а ребро – фрагменту изображения, расположенному между разрезами на узлах. Ребро графа строилось только в том случае, если полученный фрагмент мог быть распознан в качестве буквы. К полученным фрагментам изображения применялась нейронная сеть, которая присваивала каждому фрагменту соответствующую букву. Пары последовательных фрагментов объединялись в буквы тогда и только тогда, когда результаты сети совпадали (рис. 7).

Рис. 7. Пример работы нейронной сети для одного предложения различного начертания (верхние буквы – исходные изображения, нижние – результат работы сети)
Точность распознавания на тестовом множестве реализованной и использованной в данной работе модели сверточной нейронной сети составила 94,5% (рис.8).

Рис. 8. Примеры некорректной работы нейронной сети. Желаемые выходы слева направо: «d», «z», «p» (верхние буквы – исходные изображения, нижние – результат работы сети)
Заключение.
Полученный алгоритм, использующий сверточную нейронную сеть, может быть применен для решения задач оффлайн-распознавания, так как обладает достаточно высокой точностью и инвариантностью к различным искажениям и шумам. Однако, эффективность реализованной системы зависит от размера обучающей и тестовой выборок.
Точность решения поставленной задачи с использованием модели сверточной нейронной может быть улучшена практически до 100 %. Об этом подробнее написано в публикации [8].
Литература:
- An introduction to Convolutional Neural Networks. http://white.stanford.edu/teach/index.php/An_Introduction_to_Convolutional_Neural_Networks [08.07.2016]
- Keiron O'Shea, Ryan Nash. An Introduction to Convolutional Neural Networks.
- Samer Hijazi, Rishi Kumar, Chris Rowen. Using Convolutional Neural Networks for Image Recognition.
- Son Lam Phung, Abdesselam Bouzerdoum. MATLAB Library for Convolutional Neural Networks. Technical report.
- Tanzila Saba, Amjad Rehman, Ghazali Sulong. Cursive Script Segmentation With Neural Confidence // ICIC International ISSN 1349–4198. P. 4955–4964.
- Understanding Convolutions. http://colah.github.io/posts/2014–07-Understanding-Convolutions/ [08.07.2016]
- Vivek Shrivastava, Navdeep Sharma. Artificial Neural Networks Based Optical Character Recognition // Signal & Image Processing: An International Journal (SIPIJ) Vol. 3, № 5, October 2012.
- Yann LeCun, Léon Bottou, Yoshua Bengio, Patrick Haffner. Gradient-Based Learning Applied to Document Recognition // Proc. of the IEEE, November 1998.







