Вычисление расстояния до наблюдаемого объекта по изображениям со стереопары



В данной работе предлагается алгоритм для вычисления расстояния до наблюдаемого объекта по изображениям со стереопары.

Актуальность данной работы заключается в том, что определение расстояния до объекта по изображениям с двух камер — одна из ключевых задач систем компьютерного зрения. В лабораториях по всему миру ведутся исследования практического применения стереозрения для извлечения информации об окружающем мире.

Одно из применений стереозрения — навигация подвижных роботов. Например, Национальное управление по воздухоплаванию и исследованию космических пространств (НАСА) разработала робота (марсоход Mars Exploration Rover) для исследования поверхности планеты Марс. С помощью системы стереозрения робот может определять расстояние до препятствия и успешно обходить его.

Используемое вработе оборудование.

1. две USB-камеры;
2. шаблон шахматной доски размера 594 x 841 мм;
3. ноутбук с операционной системой MacOS, Python 2.7;
4. рулетка измерительная.

Подготовительные работы перед разработкой алгоритма.

1. Изготовление шаблона шахматной доски размером 594 x 841 мм на основе стандартного шаблона библиотеки с открытым исходным кодом OpenCV. Данный шаблон имеет 6 узлов по вертикали и 9 узлов по горизонтали.
2. Создание стенда из двух USB-камер, закрепленных на твердой, ровной поверхности, расположенных на фиксированном расстоянии друг от друга.

Разработка алгоритма.

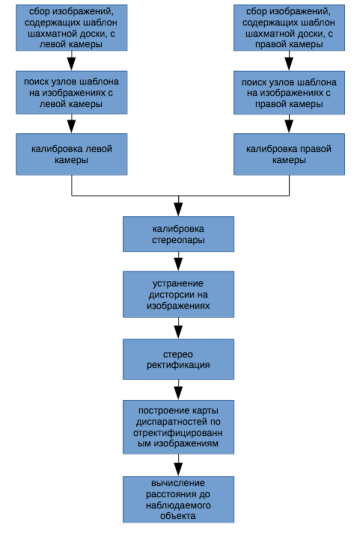
Рис. 1. Алгоритм вычисления расстояния до объекта

На рисунке 1 представлен алгоритм вычисления расстояния до наблюдаемого объекта. Приведем подробное пояснение каждого из шагов.

Шаг 1. На первом шаге производится сбор изображений, на которых изображен шаблон шахматной доски в различных положениях, с левой и правой камер стереопары. Для корректной работы реализации алгоритма необходимо, чтобы шаблон шахматной доски полностью попадал в область видимости камер стереопары и занимал как можно большую площадь кадра.

Шаг 2. На втором шаге производится поиск узлов шаблона шахматной доски на изображениях, полученных на шаге 1. Поиск узлов шаблона осуществляется при помощи библиотечной функции OpenCV find Chessboard Corners(). Координаты узлов шаблона сохраняются для дальнейшего использования.

Шаг 3. На третьем шаге производится калибровка каждой из стереопар по-отдельности. Калибровка камер стереопары осуществляется при помощи библиотечной функции OpenCV calibrate Camera().

Шаг 4. На четвертом шаге производится калибровка всей стереопары. Данные, полученные на третьем шаге подаются на вход библиотечной функции OpenCV stereo Calibrate(), которая считает внутренние параметры стереопары. После процедуры стерео калибровки мы получаем фокусное расстоянии камер в пикселях и координаты принципиальных точек камер.

Шаг 5. На пятом шаге производится устранение дисторсии на изображениях, полученных на первом шаге. Устранение дисторсии производится при помощи библиотечных функций OpenCV init Undistort Rectify Map() и remap(). После выполнения данного шага, все прямые линии наблюдаемых объектов окружающего мира становятся прямыми линиями на изображении.

Шаг 6. На шестом шаге производится ректификация изображений, полученных на шаге 5. Ректификация заключается в выравнивании деформированных изображений, полученных на шаге 5, таким образом, чтобы эпиполярные линии изображений с левой камеры совпадали с эпиполярными линиями изображений с правой камеры. Данную процедуру выполняет библиотечная функция OpenCV stereo Rectify().

Шаг 7. На седьмом шаге для каждой пары соответствующих изображений с левой и правой камер производится построение карты диспаратностей (или карты глубины (depth map)) по изображениям, полученным на шестом шаге. Каждый пиксель карты диспаратностей содержит в себе информацию о том, сколько пикселей по оси OX находится между соответствующие пикселями изображений объекта с левой и правой камер. Построение карты диспаратностей осуществляется на основе алгоритма SGBM при помощи библиотечной функции OpenCV Stereo SGBM.

Шаг 8. На восьмом шаге производится вычисление расстояния до наблюдаемого объекта. Вычисление расстояния до объекта напрямую связано с информацией, которую несет в себе карта диспаратностей, построенная на седьмом шаге.

Приведем вывод формулы для нахождения расстояния до наблюдаемого объекта.

Дано:

1. расстояние между камерами стереопары (базовое расстояние, base length)
2. фокусное расстояние камеры стереопары
3. карта диспаратностей

Найти: расстояние до наблюдаемого объекта

Решение:

– наблюдаемый объект

– расстояние между камерами стереопары (в метрах)

– фокусное расстояние камеры стереопары (в пикселях)

– координата по оси OX точки объекта P на изображении с левой камеры

– координата по оси OX точки объекта P на изображении с правой камеры

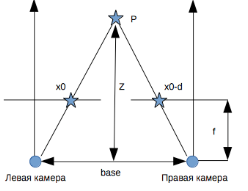
Рис. 2. Пояснительный рисунок

– диспаратность точки x0 объекта P (в пикселях)

– расстояние до наблюдаемого объекта (в метрах)

Посмотрев на Рисунок 2, можно заметить подобные треугольники. Из подобных треугольников следует соотношение:

Из данного соотношения следует, что

Получили формулу, для вычисления расстояния до наблюдаемого объекта.

Проанализировав данную формулу, можно сделать следующие выводы:

1. Расстояние до точки объекта обратно пропорционально диспаратности данной точки. Это свидетельствует о том, что точки, расположенные дальше от плоскости стереопары имеют меньшую диспаратность, нежели точки, расположенные ближе к плоскости стереопары.
2. Значение диспаратности прямо пропорционально расстоянию между камерами. Чем больше расстояние между камерами, тем выше диспаратность.
3. Разрешение карты диспаратностей линейно зависит от разрешения изображения. Чем выше разрешение изображения, тем более аккуратной получается карта диспаратностей.

Экспериментальная часть.

В данной части работы пройдемся по шагам алгоритма и рассмотрим артефакты, полученные на каждом шаге описанного выше алгоритма. Также построим зависимость ошибки определения диспаратноcтей от расстояния до наблюдаемого объекта.

Приведем наглядные иллюстрации результата работы алгоритма и построим зависимость ошибки определения диспаратноcтей от расстояния до наблюдаемого объекта.

Таблица 1

Действительные расстояния от плоскости стереопары до наблюдаемых объектов

Объект	Расстояние от стереопары до объекта (м)
Поверхность стола	2.3
Первая книга	3.11
Вторая книга	3.45
Третья книга	3.72
Доска	4.15

Таблица 2

Значения диспаратностей точек наблюдаемых объектов, взятые из карты диспаратностей

Объект	Координата точки объекта (x, y)	Значение диспаратности
Поверхность стола	(324, 274)	56.5
Первая книга	(508, 207)	42.0
Вторая книга	(415, 199)	37.6875
Третья книга	(335, 200)	35.0625
Доска	(230, 116)	31.0

Под ошибкой определения диспаратности будем понимать модуль разности значения диспаратностей, соответствующего вычисленным расстояниям (на основе базового расстояния, фокусного расстояния и значения диспаратностей) и значения диспаратностей, соответствующего действительным расстоянием.

Рис. 3. Изображение с правой камеры (этап сборки кадров с камеры с изображением шахматной доски)

Рис. 4. Изображение с левой камеры (этап сборки кадров с камеры с изображением шахматной доски)

Рис. 5. Изображение с левой камеры с найденным шаблоном (этап поиска узлов шаблона шахматной доски на изображениях)

Рис. 6. Отректифицированное изображение с правой камеры с устраненной дисторсией (этап ректификации и устранения дисторсии)

Рис. 7. Отректифицированное изображение с левой камеры с устраненной дисторсией (этап ректификации и устранения дисторсии)

Рис. 8. Изображение сцены с наблюдаемыми объектами (стол, три книги и доска, расположенные на расстоянии друг от друга)

Рис. 9. Карта диспаратностей для изображений с правой и левой камеры (стол, три книги и доска, расположенные на расстоянии друг от друга)

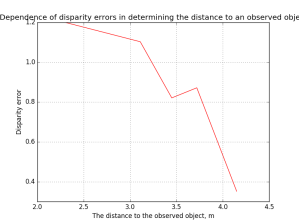
Рис. 10. Зависимость ошибки определения диспаратности от расстояния до наблюдаемого объекта

Вывод.

По графику видно, что наибольшее значение ошибки определения диспаратности для расстояния до наблюдаемого объекта от 2.30 до 4.15 метров составляет всего 1.2, что свидетельствует о хорошем качестве карты диспаратностей.

Заключение.

В данной работе был разработан алгоритм вычисления расстояния до наблюдаемого объекта по изображениям со стереопары. Приведены расчеты ошибки определения диспаратностей в зависимости от расстояния до наблюдаемого объекта.

Литература:

1. Richard Hartley, Andrew Zisserman. Multiple View Geometry in Computer Vision, 2^nd Edition
2. https://www.python.org/
3. http://opencv.org/