Sensor robot impermissible criteria in the standard positional accuracy robots plays an important role in the implementation of specific process or operation. Therefore, in this paragraph, the management of touch sensor, the robot motion on the issue of increasing positional accuracy in detail.
Sensor robot work zone in the form of a closed three-dimensional space, touching the device is closed as a result of movement in space is important to issue the necessary trajectory.
Is drawn inside the zone parallelepiped. Because the three-dimensional space is larger than the circulation figures parallelepipeddir.
Cylindrical coordinate system for robots working in the zone height and the radii of the inner form of concentric cylinders. This came to be drawn inside the inner cylinder, parallelepiped and the projection of the plain view of Figure 1 [1, 71].
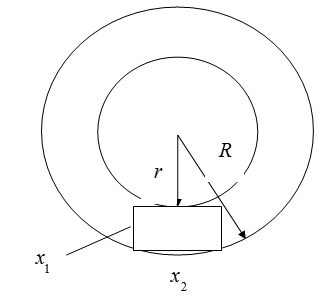
Fig. 1. Concentric cylinders and the interiorparallelepipedning plane projection
In accordance with the right sides of the rectangle ![]() and
and![]() get. The participation of the parties
get. The participation of the parties ![]() function to be formed. As a result,
function to be formed. As a result, ![]() suspended the issue of finding the maximum of the function.
suspended the issue of finding the maximum of the function.
![]()
Fig.1![]() should be.
should be.
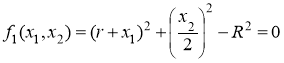
Lagranj factors such practices.
![]()
Extreme necessary conditions
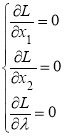
As a result, the following system of equations is formed.
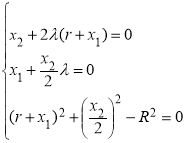
This equation system ![]() the unknowns will
the unknowns will ![]() be found. Spherical coordinate system for mobile robots is the radius of the base of the zone in view of the cylinder and sphere radius drank deeply figure. Cferik and angular coordinate system moving robots work zone analysis showed that the shape of the geometric point of view, the size of the space, draw concentric sphere figura that this parallelepiped. (Fig. 2).
be found. Spherical coordinate system for mobile robots is the radius of the base of the zone in view of the cylinder and sphere radius drank deeply figure. Cferik and angular coordinate system moving robots work zone analysis showed that the shape of the geometric point of view, the size of the space, draw concentric sphere figura that this parallelepiped. (Fig. 2).
Parallelepiped active ![]() get.
get.
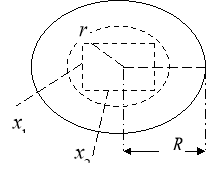
Fig. 2. Draw concentric spheres, andparallelepipedning plane projection
The issue is to find a
![]()
At the same time, ![]() you need to know.
you need to know.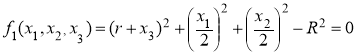
Lagranj function.
![]()
Extreme necessary conditions
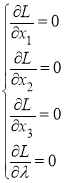
As a result, the following system of equations is formed.
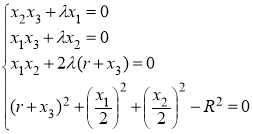
This equation system the ![]() unknowns found.
unknowns found.
Recognized by the sensor, the robot after the capture device can determine where parallelepipedning standing.
[1] parallelepipedning nine points, each point draw a small parallelepipedlar. Sensor robot motion trajectory study of the decline of the trajectory that transition into a nine point names in the chain of use [62]. Hamilton chain ordinary chain, once a nine point of the broken line trajectory. The participation of a large parallelepiped can make lots of chains of Hamilton. Therefore, it must be named Hamilton chains in the chain tanlansinki, the minimum length.
In this case, the accounting books after the chain length of at least equal to the following:
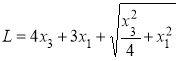
This approach has the following advantages:
‒ In the form of a sensor, the robot is the main zone is formed;
‒ Graph theory through the use of a closed three-dimensional space, trying to touch the robot trajectory is formed;
‒ Parallelepiped aspects of determining the length of the sensor, the robot does not need to express the full kinematics analytical response.
References:
- Богуславский А. А., Сербенюк Н. С., Соколов С. М. СТЗ для навигации подвижного робота по маякам на основе анализа конической проекции окружающего пространства на ТВ-камеру. Препринт ИПМ им М. В. Келдыша РАН № 78 за 2001г
- Богуславский А. А., Сербенюк Н. С., Соколов С. М. Конический сенсор для навигации подвижного робота по маякам. // Доклады научной школы-конференции «Мобильные роботы и мехатронные системы» (Москва, 5–6 декабря 2000г.). — М.: Изд-во Института механики МГУ, 2000. 42–56с.
- Платонов А. К., Сербенюк Н.С Зрительная система объезда препятствий // Доклады научной школы-конференции «Мобильные роботы и мехатронные системы» (Москва, 21–25 марта 2005г.). Часть 1.: Изд-во Института механики МГУ, 2005г 82–96с.
- Сербенюк Н. С. Система дистанционного управления робота Трикол с использованием радиоканала связи IEEE-802.11b. // Доклады научной школы-конференции «Мобильные роботы и мехатронные системы» (Москва, 17–18 ноября 2003г.).-М.: Изд-во Института механики МГУ, 2003г 77–82с.
- Охоцимский Д. Е., Платонов А. К., Сербенюк Н. С., Ярошевский B. C. Согласование колес робота «Трикол» при «вальсирующем» движении // Доклады научной школы-конференции «Мобильные роботы и мехатронные системы» (Москва, 21–25 марта 2005г.) Часть 2. Изд-во Института механики МГУ, 2005г 14–21с.
- Сербенюк Н. С., Экспериментальное исследование свойств конического сенсора. Мобильные роботы и мехатронные системы: Материалы научной школы-конференции (Москва, 5–6 декабря 2000г.). — М.: Изд-во Института механики МГУ, 2000г 56–65с.







