Адаптивное управление модульными роботами на примере многоногого робота с двумя типами конечностей



Адаптивное управление модульными роботами на примере многоногого робота сдвумя типами конечностей

Демин Александр Викторович, кандидат физико-математических наук, научный сотрудник

Институт систем информатики имени А. П. Ершова СО РАН (г. Новосибирск)

1. Введение

Гиперизбыточные робототехнические системы, такие как змеевидные и многоногие роботы, многозвенные манипуляторы, модульные роботы и др., обладают существенными преимуществами по сравнению с традиционными системами. Гиперизбыточность позволяет не только решать более широкий круг задач, но и повысить отказоустойчивость системы. Особо следует отметить активно развивающееся в последнее время направление робототехники под названием «модульные роботы» [1,2], основная идея которого заключатся в конструирование сложных роботов из множества простых однотипных модулей. Данное направление сулит целый ряд новых возможностей, начиная с создания роботов-трансформеров, меняющих свою конструкцию для решения конкретных задач, и заканчивая удешевлением производства за счет использования однотипных модулей.

Однако развитие и использование гиперизбыточных робототехнических систем сталкивается с серьезными трудностями, связанными со значительной сложностью управления подобными системами. Наличие большого количества степеней свободы делает невозможным применение традиционных подходов к созданию систем управления путем прямого задания сенсорно-моторных функций человеком-разработчиком. Поэтому становиться актуальным разработка способов автоматического порождения системы управления на основе различных моделей обучения.

В мировой практике в области адаптивного управления гиперизбыточными и модульными системами чаще всего предлагаются решения, основанные на использование популяционных методов (эволюционные методы, методы роя частиц и т. д.) в интеграции с другими известными методами машинного обучения (Reinforcement Learning, нейронные сети и др.) [3–7]. Общим недостатком подобных решений является невозможность обучения в режиме реальной работы и слабая масштабируемость относительно увеличения сложности системы (количества степеней свободы). В целом, следует отметить, что в настоящее время пока еще не предложено достаточно универсального решения задачи адаптивного управления гиперизбыточными системами.

В наших работах предлагается альтернативный подход к созданию обучающихся систем управления для модульных роботов, основанный на использовании логико-вероятностных методов извлечения знаний из данных и эксплуатации свойств функциональной симметрии элементов конструкции роботов. В соответствии с данным подходом управляющие правила системы описываются при помощи языка логики первого порядка, что позволяет использовать логико-вероятностные методы извлечения знаний из данных для обнаружения эффективных правил управления в статистических данных о взаимодействии системы с окружающим миром. В качестве основного пути для преодоления проблемы большого числа степеней свободы предлагается идея использования функциональной симметрии элементов системы, что позволяет существенно сократить пространство поиска управляющих правил за счет использования одних и тех же правил для схожих по своим функциям модулей. Интеграция логико-вероятностного подхода и свойств функциональной симметрии позволили разработать специальный метод поиска управляющих правил, который в первую очередь пытается найти правила, общие для всех модулей, а уже затем специфицировать их для каждого конкретного модуля в отдельности.

В предыдущих работах [8–11] были описаны примеры применения предложенного подхода для обучения типичных представителей простейших гиперизбыточных модульных роботов: змеевидного робота, многоногого робота и хоботовидного манипулятора. Полученные результаты продемонстрировали основные преимущества подхода: обучение и адаптацию в режиме реальной работы, высокую скорость обучения и хорошую масштабируемость относительно увеличения сложности системы. Однако рассмотренные примеры моделей роботов были ограничены тем, что их конструкции состояли из одинаковых модулей. В данной работе исследуется применимость предложенного подхода для управления модульными роботами, состоящими из разных типов модулей. С этой целью был поставлен эксперимент по обучению способам передвижения виртуальной модели простого многоногого робота, имеющего конечности двух разных типов. На примере данной модели оценивалась применимость подхода и эффективность обучения.

2. Модель обучающейся системы управления

Рассматриваемая модель системы управления представляет собой нейронную сеть, в которой базовым элементом управления является обучаемый логический нейрон. Задачей каждого логического нейрона является управление отдельным модулем робота.

Предполагается, что логические нейроны функционируют в дискретном времени . Каждый нейрон содержит некоторый набор входов , принимающих действительные значения, и один выход , принимающий значения из заранее заданного набора . В каждый момент времени на входы нейрона подается входящая информация путем присвоения входам некоторых действительных значений , . Результатом работы нейрона является выходной сигнал , , принимающий одно из возможных значений.

Работа всей совокупности нейронов определяется множеством логических правил с оценками, имеющих следующий вид:

(1)

где — переменная по объектам — индексам нейронов.

— предикаты из заданного множества входных предикатов , описывающих входы нейронов . К примеру, в простейшем случае данные предикаты могут быть заданы как , где — некоторые константы из области значении входящих сигналов, которые могут быть заданы, к примеру, путем квантования диапазона возможных значений соответствующих входов нейронов.

— предикаты из заданного множества выходных предикатов , описывающих выходы нейронов и имеющих вид , где — некоторые константы из набора значений выходных сигналов.

— предикаты из набора предикатов , заданные на множестве индексов нейронов. Смысл данного набора — сужать область применения правил вида (1) до конкретных нейронов или групп нейронов. К примеру, в простейшем случае данные предикаты могут иметь вид , где . Эти предикаты будут принимать значение «истина» только для конкретных нейронов . В эксперименте, описанном ниже, использовались предикаты и , принимающие значение «истина» соответственно только для четных либо только для нечетных индексов нейронов.

— награда, максимизация которой является постоянной задачей нейрона.

Данные закономерности предсказывают, что если на вход нейрона , будут поданы сигналы, удовлетворяющие входным предикатам из посылки правила, и нейрон подаст на свой выход сигнал, указанный в выходном предикате , то математическое ожидание награды будет равно некоторой величине .

Поясним важность введения множества предикатов . В том случае, если правила (1) не содержит предикатов из , то они будут иметь вид и будут описывать закономерности, общие для всех нейронов , . Добавление в посылку правила предиката из автоматически суживает область применения правила до какого-либо конкретного нейрона либо группы нейронов. Таким образом, правила, содержащие предикаты из , описывают закономерности, специфичные для конкретных нейронов либо групп нейронов.

Основной задачей системы управления является достижение определенной цели. По факту достижения этой цели система получает от внешней среды награду. Функция награды задается в зависимости от конечной цели и служит оценкой качества управления. Таким образом, задачей обучения системы управления является обнаружение таких правил функционирования нейронов, которые бы обеспечивали получение максимальной награды.

Для нахождения правил вида (1) используется алгоритм, основанный на идеях семантического вероятностного вывода, описанного в работах [12,13]. При помощи данного алгоритма анализируется множества данных, хранящих статистику работы нейронной сети (вход-выход нейронов и полученная награда) и извлекаются все статистически значимые закономерности вида (1). В данной работе мы не будем приводить описание алгоритма семантического вероятностного вывода. Подробное описание можно найти в работах [12,13].

Преимущество использования семантического вероятностного вывода и правил вида (1) состоит в организации поиска правил таким образом, что сначала будут обнаруживаться правила, общие для всех нейронов, а только затем — более сложные, включающие специфичные для конкретных нейронов и групп нейронов правила. В результате, в задачах управления модульными роботами, если хотя бы часть модулей имеет схожие функции, которые можно описать общими правилами, предложенный подход позволяет существенно сократить время поиска решения.

Функционирование нейронной сети в целом происходит следующим образом. На каждом такте работы сети на входы нейронов поступают входящие сигналы. После чего последовательно для каждого нейрона запускается процедура принятия решения, в процессе которой из множества правил, описывающих работу нейронов, выбираются те, которые применимы к текущему нейрону на текущих входных сигналах. Затем среди отобранных правил выбирается одно правило, прогнозирующее максимальное значение математического ожидания награды . Далее на выход нейрона подается выходной сигнал , указанный в правиле. В начальной стадии функционирования сети, когда множество правил, описывающих работу нейронов, еще пусто, либо когда нет правил, применимых к текущему набору входящих сигналов, выход нейрона определяется случайным образом. После того, как все нейроны сгенерируют свои выходные сигналы, запускаются на выполнения все действия модулей, инициируемые данными сигналами. Если в результате выполнения этих действий система достигает поставленную цель, то от внешней среды поступает награда и осуществляется обучение, в процессе которого ищутся новые и корректируются текущие правила работы в соответствии с предложенным алгоритмом поиска закономерностей.

3. Симулятор модульного робота

Эксперименты с предложенной моделью системы управления осуществлялись при помощи специально разработанного трехмерного симулятора с физическим движком, позволяющего моделировать сложные механические системы в виртуальном окружении. Программа специально создавалась для проведения экспериментов по обучению и управлению различными моделями роботов в среде, приближенной к реальному миру. Программа обладает возможностями визуализации виртуальной среды и записью экспериментов в видео-файл. В качестве физического движка в симуляторе используется открытая библиотека Open Dynamic Library (ODE) [14], которая позволяет моделировать динамику твердых тел с различными видами сочленений. Преимуществом данной библиотеке является скорость, высокая стабильность интегрирования, а также встроенное обнаружение столкновений.

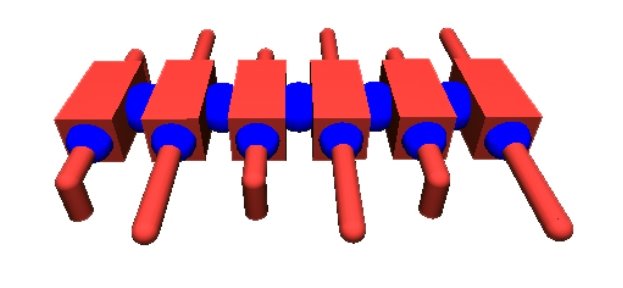
Рис. 1. Модель робота в 3D-симуляторе

Основной задачей эксперимента являлась проверка возможностей предложенной модели успешно обнаруживать эффективные управляющие правила для различных типов модулей. С этой целью в симуляторе была создана модель многоного робота, состоящая из двух повторяющихся типов модулей (рис.1). Четные модули имеют пару Г-образных конечностей с правой и левой стороны, способные двигаться только в горизонтальной плоскости. Нечетные модули имеют пару прямых конечностей, способных двигаться только в вертикальной плоскости. Модули поочередно соединены друг с другом посредством жестких сочленений. Всего робот имеет шесть модулей: три модуля с Г-образными конечностями и три — с прямыми.

Задачей системы управления являлось обучение эффективному способу движения вперед данной модели робота. Очевидно, что робот может эффективно двинуться вперед только за счет продвижения Г-образных конечностей назад. Однако поскольку Г-образная конечность может двигаться только в горизонтальной плоскости, то для того, чтобы забросить ее вперед для следующего шага и при этом не сдвинуть робота в обратном направлении, необходимо задействовать прямые конечности, чтобы приподнять робота над землей. В результате, эффективное движение робота возможно только при согласованной работе модулей разных типов. Таким образом, выбранная конструкция робота, несмотря на простоту, является хорошей тестовой моделью для проверки возможностей системы обнаруживать согласованные управляющие правила для различных типов модулей.

4. Система управления движением робота

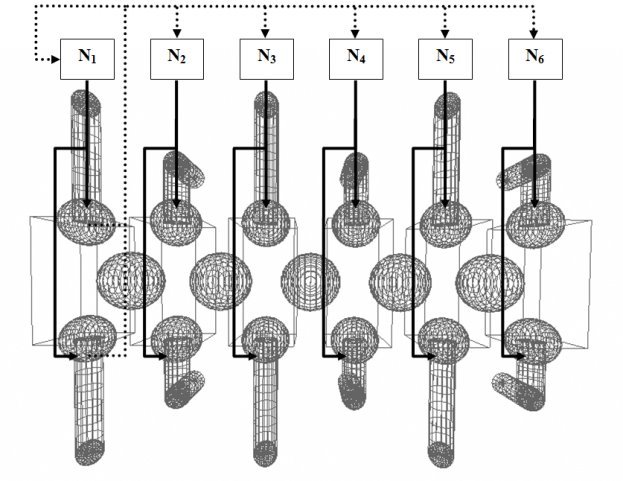
Рис. 2. Схема нейронного контура управления роботом

Схема нейронного контура, выбранного для управления роботом, состояла из шести нейронов — по одному нейрону на каждый модуль робота. Каждый нейрон , контролировал движения левой и правой конечности своего модуля, подавая активирующие сигналы на соответствующие угловые двигатели, вращающие конечности в суставе. Для упрощения задачи движения левой и правой конечностей каждого модуля были синхронизированы таким образом, что одна конечность зеркально повторяла движения другой. Таким образом, каждому нейрону достаточно было выдавать только один активирующий сигнал, чтобы привести в движение сразу обе конечности.

Первый нейрон получает на свой вход информацию о положении конечностей первого модуля. Эта же информация поступает на входы всех остальных нейронов , . Таким образом, в данной схеме состояние первого модуля, по сути, можно рассматривать как своеобразный счетчик тактов для всех остальных модулей.

Награда для системы управления рассчитывалась по факту завершения цикла выполнения шага и возврата конечностей первого модуля в исходную точку. Под шагом подразумевается вся последовательность действий, которая была выполнена в промежуток времени между текущим и предыдущим фактами нахождения конечностей в исходном состоянии. В качестве исходной точки было выбрано максимальное вертикальное положение конечностей первого модуля.

Вычисление награды осуществлялось следующим образом. Пусть в текущий момент времени положение конечностей первого модуля соответствуют исходной точке начала шага. Пусть — предыдущий момент времени, когда эти конечности находились в исходной точке. Тогда все действия в промежутке времени от до будут входить в цикл выполнения шага, а награда для этих моментов времени , где и , будет равна . Где — расстояние, которое преодолеет робот по направлению вперед за этот же промежуток времени (от до ). В случае «пустого» шага, т. е. когда и конечности первого модуля просто остаются в исходной точке два такта подряд, награда для момента времени устанавливается равной 0. Данная функция награды стимулирует систему управления находить такие последовательности действий, которые бы позволяли преодолевать как можно большее расстояние при совершении как можно меньшего числа действий.

Используя симулятор 3D-симулятор, был проведен ряд успешных экспериментов по обучению рассмотренной системы управления способам передвижения. В серии экспериментов системе управления удавалось стабильно обнаруживать правила управления, обеспечивающие согласованные движения конечностей модулей разных типов, приводящие к эффективному перемещению робота вперед. На рисунке 3 приведен пример оптимальной последовательности движений, найденной в процессе обучения.

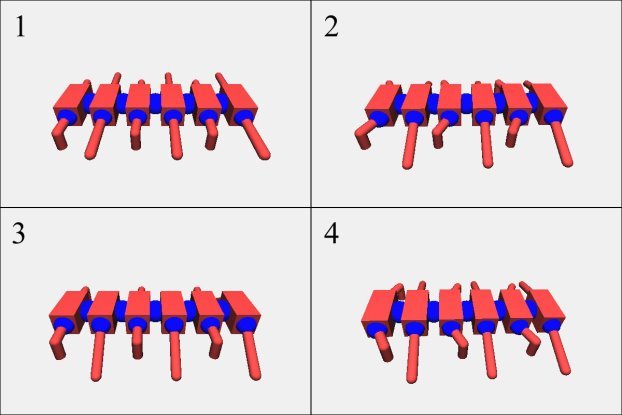
Рис. 3. Последовательность движений робота при перемещении вперед

5. Заключение

В данной работе описан новый подход к созданию обучающихся систем управления для модульных роботов, основанный на использовании свойств функциональной схожести модулей и логико-вероятностного алгоритма направленного поиска правил. Важной особенность подхода является то, что при обучении системы появляется возможность использовать не только статистические данные о ее взаимодействии со средой, но и дополнительную информацию о конструктивных особенностях самой системы, а именно: функциональную симметрию модулей. Данная возможность позволяет существенно сократить пространство поиска решений и увеличить скорость обучения. Результаты проведенного эксперимента подтвердили, что предложенный подход может быть с успехом использован для управления модульными роботами, состоящими из разных типов модулей.

6. Благодарности

Работа выполнена при финансовой поддержке гранта РФФИ № 14–07–00386.

Литература:

1. Yim M. H., Duff D. G., Roufas K. D. Modular reconfigurable robots, an approach to urban search and rescue // 1st International Workshop on Human Welfare Robotics Systems (HWRS2000). — 2000. — pp. 19–20.
2. Stoy K., Brandt D., Christensen D. J. Self-Reconfigurable robots: an introduction // Intellegent robotics and autonomous agents series. — MIT Press, 2010. — 216 p.
3. Bongard J. C. Evolutionary Robotics // Communications of the ACM. — 2013. — Vol. 56. — No. 8. — pp. 74–83.
4. Kamimura A., Kurokawa H., Yoshida E., Tomita K., Murata S., Kokaji S. Automatic locomotion pattern generation for modular robots // Proceedings of 2003 IEEE International Conference on Robotics and Automation. — 2003. — pp. 714–720.
5. Ito K., Matsuno F. Control of hyper-redundant robot using QDSEGA // Proceedings of the 41st SICE Annual Conference (2002). — 2002. — V. 3. — pp. 1499–1504.
6. Marbach D., Ijspeert A. J. Co-evolution of configuration and control for homogenous modular robots // Proceedings of the eighth conference on Intelligent Autonomous Systems (IAS8). — IOS Press, 2004. — pp. 712–719.
7. Valsalam V. K. Miikkulainen R. Modular neuroevolution for multilegged locomotion // In Proceedings of GECCO. — 2008. — pp. 265–272.
8. Демин А. В. Адаптивное управление модульным хоботовидным манипулятором // Молодой ученый. — 2016. — № 3. — С. 47–52.
9. Демин А. В. Обучающаяся система управления движением для 3D модели многоногого робота // Молодой ученый. — 2015. — № 19 (99). — С. 74–78.
10. Демин А. В. Обучение способам передвижения виртуальной модели змеевидного робота // Молодой ученый. — 2014. — № 19 (78) — С. 147–150.
11. Demin A. V. Adaptive Locomotion Control System for Modular Robots // International Journal of Automation, Control and Intelligent Systems. — 2015. — Vol. 1. — No. 4. — pp. 92–96.
12. Демин А. В. Адаптивное управление роботами с модульной конструкцией // Системы управления, связи и безопасности. — 2015. — № 4. — С. 180–197.
13. Демин А. В., Витяев Е. Е. Логическая модель адаптивной системы управления // Нейроинформатика. — 2008. — Т. 3. — № 1. — С. 79–107.
14. Smith R. Open Dynamics Engine. — URL: http://ode.org/.