Расчет потерь в обмотках электрических машин с учетом поверхностного эффекта и эффекта близости

 Показана методика расчета потерь в электрической машине с учетом поверхностного эффекта и эффекта близости проводов обмоток.

Ключевые слова: методика расчета, электрическая машина, поверхностный эффект в обмотках.

 The method of calculation of dissipation in the electrical machine is shown. The method considers skin-effect and proximity effect in windings.

Keywords: calculation method, electrical machine, skin-effect in windings.

В статье представлена методика расчета потерь в электрической машине с учетом поверхностного эффекта и эффекта близости проводов обмоток, позволяющая выбрать способ транспозиции проводов обмоток статора [1].

Для примера на рис.1а показаны три проводника, расположенные в пазу электрической машины. При использовании программного пакета ELCUT [2], который является базовым пакетом в диссертации, для расчета распределения тока по сечению проводников следует рассмотреть расчетную модель на рис.1б. Расчет проводится относительно векторного магнитного потенциала А при частоте 50 Гц. Каждый проводник имеет прямоугольное сечение 9x20 мм².

При формировании этой модели приняты следующие допущения: магнитная проницаемость стали ротора и статора обладает идеальными свойствами (линии поля магнитной индукции нормальны к поверхности стали) и электромагнитное поле имеет двумерный характер. При необходимости ELCUT позволяет учесть реальную кривую намагничивания стали.

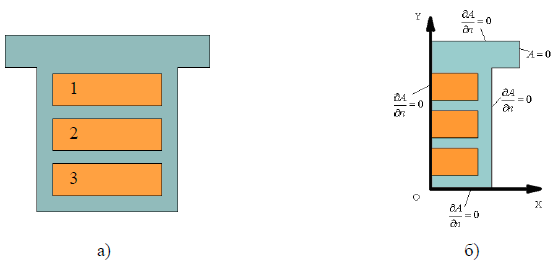
Рис.1. Проводники в пазу электрической машины (а) и расчетная модель (б)

Для численного расчета потерь необходимо рассчитать электромагнитное поле в расчетной области на рис.1б. Для этого решается уравнение Максвелла для однокомпонентного (A=A_z) комплексного векторного магнитного потенциала:

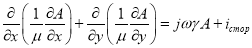, (1)

Во многих случаях уравнения электромагнитного поля необходимо решать совместно с уравнениями присоединенной электрической цепи. Закон Ома для ветви цепи, содержащей массивный проводник, помещенный в магнитное поле, имеет вид:

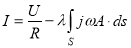(2)

где U — разность потенциалов на концах массивного проводника,

R — омическое сопротивление на постоянном токе,

S — площадь поперечного сечения проводника,

A — векторный магнитный потенциал,

ω — циклическая частота,

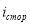 — плотность стороннего тока.

Результатом электромагнитного расчета являются локальные и интегральные значения характеристик электромагнитного поля в пазу электрической машины. Знание электромагнитного поля дает возможность определить все требуемые электромагнитные параметры. Приведем формулы, необходимые для расчета индуктивности на единицу длины обмотки 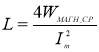[3]:

, (3)

где W_{МАГН.СР} — энергия магнитного поля на единицу длины в расчетной области,

I_m — максимальное значение тока в обмотке.

Активное сопротивление каждого провода обмотки:

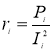, (4)

где P_i, I_i — потери и действующее значение тока.

Параметры W_{МАГН.СР}, P_i, I_i находим из списка интегральных значений, которые являются результатами расчета электромагнитного поля в ELCUT. Для примера, на рис.2 дано распределение плотности тока вдоль оси OY на рис.1б для случая параллельного соединения трех проводников при частоте 50 Гц.

Таблица 1

Результаты расчета в Elcut для рис. 1б

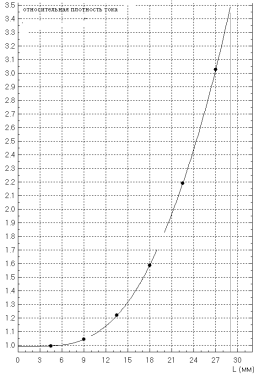
Рис. 2. Распределение плотности токов вдоль оси OY

Для оценки влияния транспозиции проводов на распределения токов между параллельными проводами обмотки учтем, что параллельно соединенные проводники подключены к одной известной ЭДС. Далее необходимо рассмотреть несколько вариантов расположения проводников в пазу, которые они поочередно занимают в зависимости от типа транспозиции. Пусть каждое взаимное расположение проводников в пазу характеризуется параметрами Li и Мi,j — собственными и взаимными индуктивностями проводников, Ri — их активными сопротивлениями. Найдем эти значения, используя комплекс ELCUT, для каждого положения проводников и затем усредним их по всей длине проводника. Тогда для определения токов 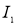, , 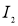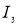в каждом из трех проводников надо записать соответствующее уравнение равновесия эдс. Например, для трех проводников в пазу имеем следующую систему уравнений:

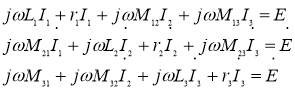, (5)

где 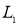, , 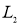, , 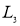, 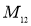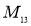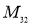4 — усредненные собственные и взаимные индуктивности проводников, расположенных в пазу.

Принимая 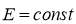, из решения системы (5) находим значения токов I1, I2, I3 и определяем потери в каждом проводе. Расчеты показали, что при условии одного изменения положения проводников на всей длине проводника (взаимно изменяется положение проводников 1 и 3), распределение токов в параллельных проводниках следующее:

Таблица 2

Результаты расчета в Elcut при транспозиции проводников 1 и 3

Результаты в таблице 2 показывают эффективность даже однократной на длине провода транспозиции для рассмотренного случая.

Литература:

1.                Сахно Л. И., Сахно О. И., Лихачев Д. И. Инженерный метод расчета критической толщины дисков обмоток трансформаторов машин контактной сварки // Сварочное производство. — 2010. — № 1. — с. 17–18.
2.                Elcut [Электронный ресурс]: сайт ООО «Тор» содержит статьи, справочную информацию, демо-версии программ для моделирования электромагнитных, тепловых и механических задач методом конечных элементов — Режим доступа: http:// www.elcut.ru; http:// www.tor.ru. — Загл. с экрана.
3.                Демирчян К. С. Теоретические основы электротехники: учебник для вузов. — СПб.: Питер, 2006. — 576 с.