В статье рассматривается математическое описание движения частицы твёрдого тела в интенсифицированном кипящем слое. Показана целесообразность применения модели взаимопроникающей среды с учётом сил сцепления твердых частиц с несущей средой и сил взаимодействия между частицами.
Приводятся уравнения движения и уравнение неразрывности потока. Решения этих замкнутых дифференциальных уравнений даёт возможность точного определения параметров потока, необходимых при рассмотрении процессов горения твердых топлив.
Ключевые слова: кипящий слой, подъемная сила, сжигание ископаемого органического топлива, фонтанирующий и вихревой слой, гидродинамические параметры.
Изучение и анализ литературных источников показывает, что большое количество выбросов в атмосферу вредных газов, в том числе вследствие деятельности человека, приводит к общему изменению климата на планете и увеличению «парникового» эффекта, образованию пыльных бурь и сопутствующих им, является глобальным экологическим проблемам. Как известно, более половины всей электроэнергии, получаемой на электростанциях мира, производится за счет сжигания ископаемого органического топлива. В целом на органическом топливе вырабатывается около 62 % всей электроэнергии. Причем, больше половины её вырабатывается на электростанциях, работающих на природном газе.
В настоящее время намечается тенденция по устранению сложившейся диспропорции в использовании видов энергоресурсов с повышением эффективности их использования [1]
В перспективе ожидается повышение роли твердого топлива. К 2020 году каждый третий киловатт-час электроэнергии в мире будет выработан на угольной электростанции [2].
В связи с этим ещё более обостряется проблема загрязнения окружающей среды, и особенно почвы, вредными выбросами. Ветер и загрязнённые облака разносят вредные вещества на огромные территории, в том числе и на сельхозугодья, что приводит к снижению урожайности сельхоз культур, а то и вовсе приводит к непригодности угодий.
Проведение фундаментальных исследований и создание математической модели требуемой гидродинамической обстановки позволит в дальнейшем обеспечить эффективное проведение топочных процессов при сжигании твердых топлив в условиях взвешенного состояния, а именно кипящего, фонтанирующего и вихревого слоях, с последующей выдачей расчетных формул для интенсификации процесса горения.
Поэтому, для полного описания движения частиц в интенсифицированном кипящем слое с учетом результатов работ [3,4], целесообразно рассматривать модель взаимопроникающей, взаимодействующей, многофазной, и многокомпонентной среды с учетом подъемных сил Жуковского — Магнуса, сил сцепления твердых частиц и других сил взаимодействия подвижных частиц и потока, а также силы трения [5].
Тогда уравнения движения, описывающие указанные процессы с учетом силы тяжести, подъемной силы Жуковского — Магнуса и силы взаимодействия между частицами будут иметь следующий вид:
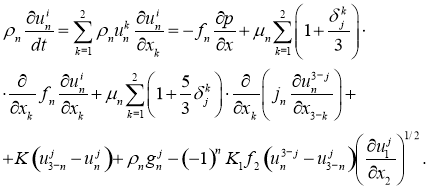(1)
Уравнение неразрывности
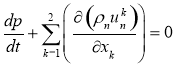(2)
, (3)
где 
компонента скорости n-й фазы; 
-коэффициент взаимодействия между фазами, p-давления, 
-объемное содержание n-й фазы; 
- приведенная и истинные плотности n-й фазы соответственно; 
-коэффициент динамической вязкости n-й фазы; 
компонента массовой силы n-й фазы; 
кинематическая вязкость первой фазы (жидкий) 
-символ Кронекера; 
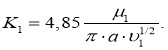
Прежде всего, о подъёмной силе в двухфазном потоке. При ламинарном режиме движения смесей по вертикальной трубе миграция частиц в поперечном сечении трубы возникает при наличии радиальной силы, в данном случае — подъемной силы Жуковского — Магнуса.
Как известно, эта сила появляется при обтекании тела градиентным потоком жидкости. Анализ процесса обтекания одиночной частицы потоком вязкой жидкости внутри трубы показывает, что в восходящем потоке, когда 
скорость твердых частиц меньше скорости жидкости, поток жидкости будет обтекать частицу. При этом направление набегающего потока совпадает с направлением общего потока. Градиент скорости при этом обусловливает одновременно два процесса:
1) вокруг частицы образуется несимметричное поле скоростей, в результате появляется подъемная сила, направленная к оси трубы;
2) вследствие эффекта Магнуса образуется подъемная сила, также направленная к оси трубы.
Р. Сэфман теоретически определил подъемную силу, действующую на сферическую частицу со стороны вязкой жидкости в сдвиговом потоке. Эта сила нормально направлена к направлению потока и при градиенте скорости —
имеет вид:
, (4)
где: a — радиус сферической частицы.
Если 
, сила имеет противоположное направление.
Если число частиц в элементарном объеме σ равно n, общая подъемная сила равна nG. После приведения к единичному объему подъемная сила имеет вид 
Если через σ2обозначить объем частиц в элементарном объеме, получим:
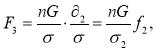(5)
где: 
— объемное содержание твердых частиц.
При 
имеем
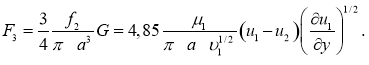(6)
В уравнения взаимопроникающего движения многофазных сред (6) входят члены, отражающие силовое взаимодействие между фазами, тепловое взаимодействие, фазовые превращения и. т.д.
Сила взаимодействия между фазами, в свою очередь, включает силу, возникающую из-за расширения потока в трубе; силу трения между фазами; силу, возникающую из-за ускоренного движения включений относительно несущей среды; силу дополнительного воздействия на включения за счет градиента поля средних скоростей несущей фазы- сила Жуковского — Магнуса.
Система уравнений (1–3) хотя и написана для многофазных сред, является замкнутой, относительно неизвестных функций от двух независимых переменных. Решение данной системы уравнений, при соответствующих начальных и граничных условиях, можно получить численным и аналитическими методами или методом линеаризации.
1). Рассмотрим движение одиночной частицы в воздушном потоке. Форму частицы считаем шарообразной, плотность частицы 
-больше плотности воздуха и с числом Рейнольдса:
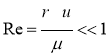, (7)
где: 
-скорость набегающего потока. 
–радиус частиц. Тогда динамику движения частиц можно описать уравнениями системы (1–3).
В результате получим
(8)
где u2 -искомая скорость движения частиц; 
скорость патока ветра; 
- время. Удовлетворяющее условию при 
решении уравнения (8) будет иметь вид:
, (9)
где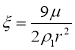 
откуда видно, что с увеличением 
значение u2 монотонно растет от нуля, асимптотически приближаясь к 
при 
Приводим график изменения скорости фаз и концентрации на основе полученного аналитического решения (рис. 1).
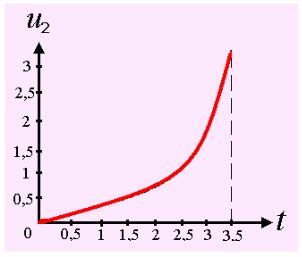
Рис. 1. Зависимость степени изменения скорости твердых частиц от времени, где пунктирная линия есть
На основе анализа результатов установлено, что на характер движения частиц и газа в вертикальном потоке влияют силы различной природы: силы гравитации, присоединенных масс, поперечные силы Сэфмана. В результате проведенных численных расчетов определены гидродинамические параметры: скорость, давление и концентрация фаз.
Литература:
- Мухиддинов Д. Н. Разработка энерготехнологии сжигания Ангренского бурого угля. //Проблемы энерго-и ресурсосбережения. № 1–2. Ташкент. 2010. С. 90–96.
- Аллаев К. Р. Перспективы развития энергетики мира и Узбекистана // Сборник трудов Международной научно-технической конференции «Современное состояние и перспективы развития энергетики». -Ташкент 2011. С.11–14.
- Бабаходжаев Р. П., Каримов А. А., Шакиров А. А., Гидродинамические исследования двухфазного фонтанирующего слоя в коническом аппарате //Вестник ТашГТУ. № 3,4, Ташкент, 2009, с. 79–82.
- Бабаходжаев Р.П, Шакиров А. А., Каримов А,А, Пулатова Д. М. Движения твердой частицы в восходящем потоке газа в камере сгорания конической формы. //Проблемы информатики и энергетики. № 1. 2012. Ташкент. С. 45–48.
- Бабаходжаев Р. П., Шакиров А. А., Каримов А,А, Пулатова Д. М. Исследование течения газа в слое дисперсного материала в зависимости от скорости газа // «Энерго-и ресурсосбережение в теплоэнергетике и социальной сфере». Международная научно- техническая конференция. Южно-Уральский ГУ.-Челябинск, 2013.
