На примере электровосстановления йода рассмотрена теория проточно-инжекционных амперометрических систем с трубчатыми угольными электродами. Показана зависимость аналитического сигнала амперометрического датчика от концентрации йода, гидродинамического режима, скорости истечения жидкости, длины электрода, ионной силы раствора.
Проводятся практические рекомендации для конструирования амперометрического проточно-инжекционного анализатора с трубчатыми углеграфитовыми электродами.
Ключевые слова: проточно-инжекционные системы; трубчатые электроды; гидродинамический режим; углеграфитовые электроды; параметры электрода; амперометрический датчик; аналитический сигнал; йода определение.
Проточно-инжекционные аналитические системы благодаря их универсальности, производительности, точности измерений, гибкости в решении разнообразных практических задач находят все большее применение в различных отраслях промышленности, медико-биологических и научных исследованиях, где необходимо за короткий срок осуществить значительное количество рутинных анализов [13,14].
В основе проточно-инжекционных методов лежит осуществление возможности анализа вещества, введенного с помощью дозирующего устройства в сегментированный поток жидкости. Аналитический сигнал, как правило, записывается регистрирующим устройством в виде пика, величина которого может быть сравнена с величиной пика эталонного образца.
Проточно-инжекционный анализ, предложенный Ружичкой и Хансеном в 1975 году, в настоящее время продолжает совершенствоваться, оснащаясь современной измерительной базой, включающей спектрофотометрические, хроматографические, рефрактометрические и электрохимические методы анализа и соответствующие детекторы [1,9].
Из всех перечисленных способов детекции, электрохимическая представляется наиболее оптимальной, так как она сравнительно недорога и позволяет осуществить простую автоматизацию аналитической системы в целом [2]. Электрохимические детекторы подразделяются на следующие классы:
кондуктометрические — измеряющие изменение электропроводности в потоке – жидкости носителе при введении в систему анализируемого образца;
потенциометрические — изменение потенциала индикаторного электрода в соответствии с уравнением Нернста;
кулонометрические — основанные на измерении (сравнении) количества электричества, прошедшего через электрохимическую ячейку без и в присутствии анализируемого вещества;
амперометрические — в которых аналитический сигнал выражается в виде силы тока.
Для последних известны разнообразные датчики, отличающиеся друг от друга, как конструктивными особенностями электрохимической ячейки, так и материалом и формой измерительных электродов.
В настоящей работе нами представлены проточно-инжекционные системы с трубчатыми электродами и проведено математическое описание процесса.
Материалы и методы
В работе были использованы электроды из углеграфита спектральной чистоты СУ-3. Согласно ТУ 01–7-67 электроды из угля для спектрального анализа марки СУ-3 выпускаются длиной 200 мм и диаметром 6±0,2 мм. Этот материал содержит только следовые количества (< 10–5 %) железа, алюминия, бора, меди, марганца, магния и кальция.
Для изготовления рабочего углеграфитового электрода с однородной поверхностью поступали следующим образом: электроды СУ-3 перемалывали в электромельнице до состояния пудры, просеивали через сито с ячейками 0,1–0,08 мм (200–300 меш). Отсеянную массу углеграфита при перемешивании малыми порциями вносили в расплавленный парафин в соотношении 50:50. Расплавленную смесь загружали в медные тонкостенные трубочки диаметром 6 мм, предварительно зачищенных и обработанных раствором азотной кислоты с последующей промывкой дистиллированной водой. После застывания углепарафиновой смеси и ее «старения» в течение 24–48 часов, просверливали канал диаметром 1 мм по всей длине электродной заготовки, который полировали пропущенной через него хлопчатобумажной нитью. Полученные электроды использовали в проточном датчике в паре с хлорсеребряным электродом сравнения ЭВЛ-1-М3.
В качестве модельной реакции использовалась йод-йодидная окислительно-восстановительная пара, позволяющая осуществить гальванический режим работы амперометрического датчика [7].
Растворы с заданной концентрацией йода готовили разведением фиксанала йода. Концентрацию исходного раствора йода устанавливали титриметрическим методом [8]. Калибровочные растворы йода с концентрацией менее 10–3 М готовили ежедневно.
Потенциометрические измерения включали определение рН буферных и анализируемых растворов. Для определения рН служил иономер И-130 со стеклянным электродом ЭСЛ-43–07 и автоматической компенсацией изменения температуры. Погрешность измерения не превышала ± 0,02 рН в диапазоне измерений рН 3,0–8,5.
С целью теоретического описания процессов, протекающих в канале трубчатого электрода было изучено влияние гидродинамического режима, скорости истечения жидкости и длины электрода на аналитический сигнал датчика.
Результаты и обсуждение
Для интенсификации электрохимического процесса необходимо использовать электроды с развитой поверхностью. Этого можно добиться, увеличивая геометрические параметры электрода, изменяя его конфигурацию или используя пористые электроды.
Исследование механизма генерации тока в пористых электродах представляет собой значительные трудности [12]. Это связано с тем, что суммарный ток, снимаемый с пористого электрода, является результатом наложения целого ряда процессов, таких, как локальная кинетика электрохимической реакции, диффузия, конвекция и т. д. На гладком электроде, работающем в режиме смешанной кинетики, все эти процессы образуют цепь из последовательно соединенных элементов, так что практически не существует возможность выделить основную стадию электрохимического процесса. В пористых электродах, в силу эффекта неравнодоступности процесс носит не локальный, как на гладком электроде, а распределенный характер, который может меняться при удалении от внешней поверхности электрода вглубь пористой среды [11]. Кроме того, нет возможности разделить омические, активационные или другие ограничения и выделить из них одну лимитирующую стадию. Положение дополнительно осложняется тем, что все эти явления протекают в пористой среде, имеющей различные по величине и геометрической конфигурации параметры. Поэтому метод описания процессов, протекающих в пористой токопроводящей среде, может носить только частный характер, соответствующий только для данной конфигурации пор [6]. В более общем случае теоретическое описание пористой среды — задача практически безнадежная.
В связи с этим большинство исследователей при использовании в аналитических системах пористых электродов применяют эмпирические зависимости тока, генерируемого пористым электродом, от концентрации вещества [3,4]. Это затрудняет метрологическую оценку электрохимического датчика, так как трудно добиться унификации характеристик анализаторов с пористыми индикаторными электродами из различных партий материала. Кроме того, из-за наличия пор, возможно образование застойных зон, ухудшающих гидродинамические характеристики проточных датчиков. А если учесть, что электрохимический процесс экспоненциально затухает по глубине электрода, то для быстрых обратимых электрохимических процессов вообще не целесообразно иметь электроды с большой пористостью [11].
При одинаковых геометрических размерах наибольшей поверхностью будут обладать трубчатые электроды. Они удобны и просты в эксплуатации и хорошо поддаются теоретическому описанию. В связи с этим конструкция разрабатываемого нами проточного амперометрического датчика для определения йода основана на использовании трубчатого угольного измерительного электрода.
На рисунке 1 показана принципиальная схема амперометрического проточно-инжекционного анализатора с трубчатым электродом.
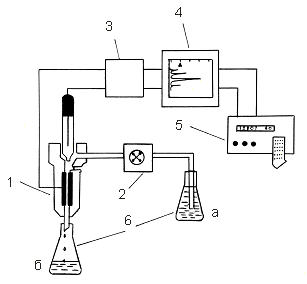
Рис. 1. Принципиальная схема проточно-инжекционного анализатора с трубчатым электродом: 1 — проточный амперометрический датчик; 2 — перистальтический насос; 3 — компенсатор-усилитель; 4 — регистратор; 5 — интегратор тока; 6 — емкости для рабочего (а) и отработанного (б) электролитов
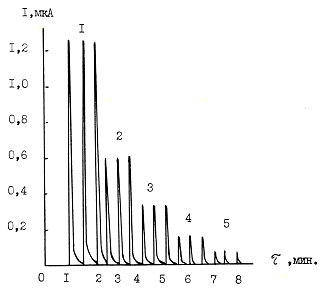
Рис. 2. Запись катодных пиков на диаграммной ленте самопищущего потенциометра для различных концентраций йода: 1–10–5 М J2; 2–5·10–6 М J2; 3–2,5·10–6 М J2; 4–1,25 ·10–6 М J2; 5–0,6 · 10–6 М J2
Анализатор содержит перистальтический насос (I), двухэлектродный амперометрический датчик с трубчатым угольным (а) и хлорсеребряным вспомогательным (б) электродами (2), делитель напряжения — компенсатор (3), потенциометр КСП-4 (4), с подключенным интегратором тока (5). Рабочий и вспомогательный электроды заключены в единый корпус из органического стекла. Ввод пробы в измерительную камеру датчика осуществляется через резиновую прокладку клапана с помощью автоматического микродозатора пипеточного типа.
Принцип работы датчика можно описать следующим образом. Проба, содержащая электрохимически активное вещество, инжектируется с помощью микродозатора в движущийся с постоянной скоростью поток фонового электролита, поступает в канал угольного трубчатого электрода, диффундирует к внутренней поверхности электрода и деполяризует его, что вызывает изменение тока во внешней цепи анализатора, отмечаемое на диаграммной ленте самописца и виде пика (рис.2).
С целью теоретического описания процессов, протекающих в канале трубчатого электрода, нами рассмотрены следующие положения:
Предположим, что электрохимически активное вещество восстанавливается (окисляется) в канале трубчатого электрода
А ± nе- → В (1)
Тогда предельный ток этой реакции может служить мерой концентрации этого вещества в анализируемом растворе и, применяя уравнение Фарадея, получим [5]:
![]() (2)
(2)
где I — ток амперометрического датчика, А; n — количество электронов, участвующих в единичном электрохимическом акте; F — число Фарадея (96500 А·сек/Моль); ![]() -- число молей активного вещества, реагирующего в единицу времени t в канале трубчатого электрода.
-- число молей активного вещества, реагирующего в единицу времени t в канале трубчатого электрода.
При ламинарном потоке жидкости весь поток можно рассматривать как бы состоящий из двух частей — входного участка h и области установившегося ламинарного течения (Рис.3).
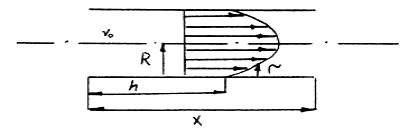
Рис. 3. Профиль скорости движущейся жидкости в канале трубчатого электрода (ламинарный поток). h — входной гидродинамический участок
В первом участке, движущаяся жидкость, содержащая анализируемую пробу, испытывает тормозящее действие стенок. В результате чего прямолинейный участок профиля преобразуется в пуазелевский или ламинарный, который соблюдается при значении чисел Рейнольдса < 2300 [15]. Длина входного участка приблизительно может быть оценена по формуле [10]:
h ~ 0,1·R·Re(3)
где R- радиус канала электрода; Re — число Рейнольдса.
После этой точки можно считать, что формирование профиля скорости ламинарного течения закончено, и дальнейшее течение жидкости происходит вдоль оси канала электрода с параболическим профилем скорости, характеризуемой формулой:
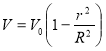 (4)
(4)
где![]() — максимальная скорость течения жидкости в трубчатом электроде при r = 0, т. е. в центре, Δp — перепад давления на длине X. В связи с этим процесс диффузии происходит на малых расстояниях от стенки трубчатого электрода, при r ~ R.
— максимальная скорость течения жидкости в трубчатом электроде при r = 0, т. е. в центре, Δp — перепад давления на длине X. В связи с этим процесс диффузии происходит на малых расстояниях от стенки трубчатого электрода, при r ~ R.
Если ввести новую переменную у= R — r и ограничиться малыми ее значениями, то имеем: ![]() (5)
(5)
Уравнение конвективной диффузии по В. Г. Левичу [10] будет иметь вид:
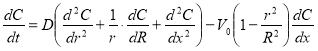 (6)
(6)
где С — концентрация вещества;
D — поток диффузии;
R и r — радиус и расстояние от стенки трубчатого электрода.
Граничные условия при решении этого уравнения относительно предельного диффузионного потока будут
С → С0 при r → ∞ и С = 0 при r = 0
Это уравнение может быть решено введением безразмерной величины [15]
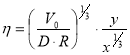 (7)
(7)
при этом связь С с новой переменной будет:
![]() (8)
(8)
Решение последнего уравнения при граничных условиях приводит к следующему выражению:
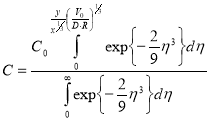 (9)
(9)
Плотность диффузионного потока на стенку трубчатого электрода может быть описана уравнением:
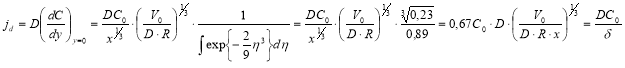 (10)
(10)
где δ- толщина диффузионного слоя: 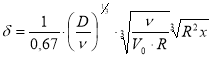 (11)
(11)
Полный диффузионный поток на внутреннюю поверхность электрода описывается уравнением:
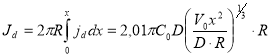 (12)
(12)
С учетом этого уравнения ток, генерируемый трубчатым электродом, описывается уравнением:
![]() (13)
(13)
а так как V0 может быть представлено соотношением
![]() , где Q — расход жидкости см3/сек,
, где Q — расход жидкости см3/сек,
уравнение (13) принимает вид
![]() (14)
(14)
Из полученного уравнения следует, что величина выходного сигнала датчика зависит от длины электрода, скорости движения фонового электролита (подвижной фазы), концентрации электроактивного вещества и коэффициента диффузии.
Эти параметры являются определяющими при расчете конструкции проточного амперометрического датчика с трубчатым электродом.
С учетом эффективности электролиза, работа амперометрического датчика с трубчатым электродом описывается уравнением:
![]() (15)
(15)
где C0 и Сх — концентрация вещества на входе и выходе из трубчатого электрода,
соответственно, и θ — эффективность электролиза: ![]()
С целью экспериментального подтверждения соответствия математической модели датчика и условия ее выполнимости, нами были изготовлены датчики с угольными индикаторными электродами различной длины и диаметра канала 0,1 см.
В таблице 1 сведены результаты экспериментальных исследований:
Таблица 1
Значения величины тока (мкА) амперометрического датчика при различной концентрации йода и длины индикаторного трубчатого электрода* (n = 5,Р = 0,95)
|
СJ2, мкМ |
2см |
3 см |
4 см |
|
1,0 |
0,07± 0,01 |
0,07 ± 0,01 |
0,09 ±0,01 |
|
2,5 |
0,14± 0,01 |
0,17 ± 0,01 |
0,23±0,03 |
|
5,0 |
0,29± 0,03 |
0,34 ± 0,02 |
0,46±0,02 |
|
8,0 |
0,53± 0,05 |
0,54 ± 0,04 |
- |
|
10,0 |
0,66± 0,04 |
0,63 ± 0,08 |
0,87±0,04 |
|
20,0 |
1,19± 0,03 |
1,40 ± 0,12 |
1,55±0,04 |
*- Условия: скорость течения фонового электролита 120 см3/час; электролит — натрий-ацетатный буфер, рН 4,0; ϻ = 0,4 М; объем вводимой пробы 0,1 см3; температура 21°С.
Анализ экспериментальных данных показал, что связь амперометрического сигнала датчика при различных концентрациях электрохимически активного вещества и длины электрода описывается функциональной зависимостью: ![]() .
.
На рисунке 4 показаны экспериментальные и теоретические зависимости выходного сигнала датчика от скорости движения раствора электролита.
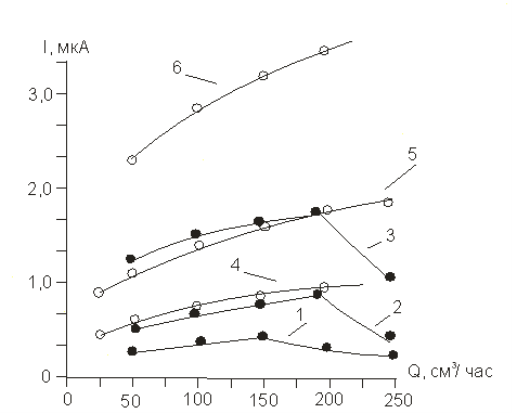
Рис. 4. Зависимость амперометрического сигнала датчика от скорости течения раствора электролита: ● — экспериментальная зависимость, ○ — теоретическая зависимость. 1 и 4 — для СJ2 0,25 · 10–5 М, 2 и 5 — для СJ2 0,50 · 10–5 М, 3 и 6 — для СJ2 1,00 · 10–5 М
В интервале скоростей течения подвижной фазы от 50 до 150 см3/час для электродов с внутренним диаметром 0,1 см и длиной 2–4 см зависимость силы тока i от Q при различных концентрациях электроактивного вещества имеет вид ![]() в соответствии с уравнением (14). Однако, абсолютные величины этих токов для экспериментальных (1–3) и теоретических (4–6) кривых различны. Это объясняется тем, что амперометрический датчик работает в режиме кинетических токов, в то время как уравнение (14) описывает зависимость предельного тока от концентрации иода и параметров датчика. При скорости движения электролита от 200 см3/час и более зависимость
в соответствии с уравнением (14). Однако, абсолютные величины этих токов для экспериментальных (1–3) и теоретических (4–6) кривых различны. Это объясняется тем, что амперометрический датчик работает в режиме кинетических токов, в то время как уравнение (14) описывает зависимость предельного тока от концентрации иода и параметров датчика. При скорости движения электролита от 200 см3/час и более зависимость ![]() не может быть описана уравнением (14) для изученных электродов. Очевидно, в этих интервалах для рассматриваемых электродов осуществляется переход гидродинамического режима из ламинарного в турбулентный (см. таблицу 2).
не может быть описана уравнением (14) для изученных электродов. Очевидно, в этих интервалах для рассматриваемых электродов осуществляется переход гидродинамического режима из ламинарного в турбулентный (см. таблицу 2).
Таблица 2
Расчетные значения числа Рейнольдса* при различных скоростях течения раствора электролитах
|
Q, cм3/час |
Длина трубчатого угольного электрода, см |
||
|
2,0 |
3,0 |
4,0 |
|
|
50 |
354 |
530 |
706 |
|
100 |
708 |
1060 |
1412 |
|
120 |
849 |
1274 |
1698 |
|
150 |
1062 |
1590 |
2118 |
|
200 |
1416 |
2120 |
2824 |
|
250 |
1770 |
2650 |
3530 |
|
500 |
3540 |
5300 |
7060 |
|
1000 |
7080 |
10600 |
14120 |
*- число Рейнольдса может быть рассчитано по формуле:
Q — скорость движения жидкости см3/сек;
Х — длина электрода, см;
R — радиус канала электрода, см;
ν — кинематическая вязкость,см2/сек (для водных растворов ν = 0,01 см2/сек).
** — заливка серым цветом показывает значения чисел Рейнолдса, соответствующих переходу ламинарного гидродинамического режима в турбулентный.
В уравнение зависимости силы тока от концентрации электроактивного вещества и параметров датчика не входят значения радиуса канала электрода и, может показаться, что его величина не влияет на величину амперометрического сигнала. Однако, следует отметить, что расход фонового электролита и величина входного гидродинамического участка, а следовательно, и характер гидродинамического режима, тесно связаны с диаметром канала трубчатого электрода. Можно предположить, что стабильную и воспроизводимую работу датчика следует ожидать при условиях установившегося гидродинамического и диффузионного режимов (h и Н — соответственно). Длина участка установившегося диффузионного режима приближенно может быть рассчитана по формуле [10]: ![]() (16)
(16)
где Pr — число Прандля 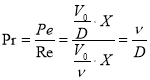 (17)
(17)
Ре — число Пекле; X — длина канала электрода; ν — кинематическая вязкость.
Таким образом, подставляя выражения чисел Рейнольдса и Прандля, имеем:
Из полученного соотношения следует, что значение Н — настолько велико, что вся длина трубчатого электрода недостаточна для установления диффузионного режима. Поэтому остается лишь попытаться установить гидродинамический режим за счет уменьшения длины входного гидродинамического участка. Очевидно, этого можно добиться путем понижения числа Рейнольдса, увеличивая радиус входного участка канала электрода. Таким образом, параметры и конфигурация трубчатого электрода находятся в тесной взаимосвязи с гидродинамическим режимом, а, следовательно, и с такими метрологическими характеристиками, как воспроизводимость, диапазон линейности градуировочного графика и коэффициент чувствительности анализатора.
Таблица 3
Зависимость сигнала датчика от конфигурации канала трубчатого электрода (n= 3, Р =0,95)
|
№ |
Профиль канала электрода |
СJ2, мкМ |
Iсред.±Δi,мкА |
sr |
|
I |
s = 0,94 см3 |
2,5 |
0,17 ±0,01 |
0,059 |
|
5,0 |
0,29±0,03 |
0,138 |
||
|
10,0 |
0,63±0,04 |
0,129 |
||
|
20,0 |
1,03±0,08 |
0,143 |
||
|
II |
s = 1,88 см3 |
2,5 |
0,42±0,02 |
0,071 |
|
III |
s = 1,1 см3 |
2,5 |
0,32 ± 0,01 |
0,063 |
|
5,0 |
0,72±0,04 |
0,083 |
||
|
10,0 |
1,11±0,03 |
0,072 |
||
|
20,0 |
1,63±0,08 |
0,074 |
||
|
30,0 |
2,12±0,10 |
0,075 |
||
|
IV |
s=1,25 см3 |
2,5 |
0,36±0,02 |
0,083 |
|
5,0 |
0,70±0,03 |
0,057 |
||
|
10,0 |
1,22±0,06 |
0,073 |
||
|
20,0 |
1,92±0,07 |
0,057 |
||
|
30,0 |
2,49±0,08 |
0,048 |
||
|
V |
s =1,57 см3 |
2,5 |
0,40 ± 0,01 |
0,091 |
|
5,0 |
0,79±0,04 |
0,062 |
||
|
10,0 |
1,36 ± 0,09 |
0,043 |
||
|
20,0 |
2,51± 0,07 |
0,056 |
||
|
30,0 |
2,72± 0,07 |
0,029 |
||
|
5,0 |
0,68±0,08 |
0,132 |
||
|
10,0 |
1,19±0,06 |
0,059 |
Анализ экспериментальных и расчетных данных показал, что в качестве измерительного наиболее целесообразно использовать трубчатый электрод длиной 3 см. Он обладает большой поверхностью для высокочувствительного определения J2 и имеет широкий диапазон скоростей течения фонового электролита для осуществления ламинарного гидродинамического режима (см. таблицу 2). В связи с этим на основе использования в качестве измерительного — трубчатого электрода длиной 3 см нами была изучена зависимость сигнала датчика от концентрации йода с электродами различной конфигурации. Некоторые экспериментальные данные приведены в таблице 3.
Из таблицы 3 видно, что улучшенными метрологическими характеристиками обладают электроды IV и V с кажущейся внутренней поверхностью 1,25 см2 и 1,57 см2. В то же время последний из них ввиду несколько большей поверхности обладает более высокой чувствительностью и широким диапазоном линейности градуировочного графика. В связи с этим, все дальнейшие доработки конструкции датчика проводили с использованием трубчатого электрода длиной 3 см и с переменным диаметром канала: 0,2 х 2,0 и 0,1 х 1,0 см.
В таблице 4 показана зависимость выходного сигнала датчика с таким трубчатым электродом от концентрации йода, на основании которой строится градуировочный график.
Таблица 4
Величина выходного сигнала датчика (мкА) для различных концентраций йода (мкМоль/л). n = 3, Р = 0,95
|
СJ2, мкМ |
I ±Δi,мкА |
sr |
|
0,5 |
0,06 ±0,01 |
0,056 |
|
1,0 |
0,12 ±0,01 |
0,048 |
|
2,5 |
0,32 ±0,01 |
0,031 |
|
5,0 |
0,65 ±0,01 |
0,031 |
|
8,0 |
1,08 ±0,02 |
0,028 |
|
10,0 |
1,28 ±0,02 |
0,028 |
|
15,0 |
1,82 ±0,02 |
0,016 |
|
20,0 |
2,48 ±0,05 |
0,020 |
|
30,0 |
3,52 ±0,06 |
0,040 |
Градуировочная зависимость сигнала амперометрического датчика с таким трубчатым электродом от концентрации вводимого раствора иода описывается корреляционным уравнением: I = 0,0506 + 0,1182 С.
Одним из факторов, определяющих чувствительность гальванического амперометрического датчика, является ЭДС: ![]() ,
,
где R — внутреннее сопротивление датчика;r — сопротивление внешней цепи.
Величина ЭДC определяется свойствами материала электрода, ионной силой раствора электролита, температурой.
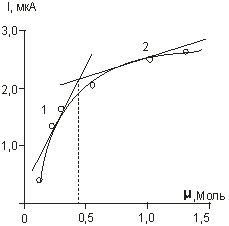
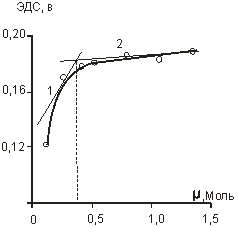
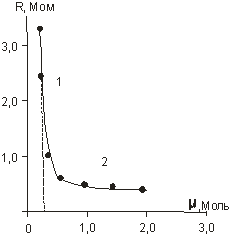
Нами изучена зависимость ЭДС, R, выходного сигнала датчика от ионной силы раствора фонового электролита.
На рисунке 5 представлены эти зависимости и каждая из них описана с использованием математической статистики.
|
|
|
|
а |
б |
|
|
I1 = 0,4144 + 5,1285 ϻ I2 = 1,3360 + 0,9709 ϻ
ЭДС1 = 0,0974 + 0,2128 ϻ ЭДС2 = 0,1731 + 0,0120 ϻ
R1 = 5,4645–12,3062 ϻ R2 = 0,5755–0,0837 ϻ |
|
в |
Рис. 5. Зависимость выходного сигнала датчика (а), ЭДС (б) и внутреннего сопротивления R (в) от ионной силы раствора фонового электролита
Ввиду невозможности описания экспериментальных данных одним уравнением первого или второго порядка для каждой зависимости выведено два линейных уравнения. Сравнение коэффициентов уравнений, рассчитанных методом наименьших квадратов, показало, что в каждом случае наблюдается взаимосвязь тока, ЭДС, внутреннего сопротивления датчика от величины ионной силы фонового электролита. Причем, общей точкой, удовлетворяющей описание ветвей экспериментальных кривых, является ионная сила раствора ~ 0,4 М, что соответствует нашему выводу о влиянии общей ионной силы раствора на электрохимические процессы, сделанному при изучении кинетики восстановления йода на угольном электроде [6].
Выводы
Проведенное исследование позволило сделать следующие практические выводы для электрохимического определения йода с помощью амперометрического проточно-инжекционного анализатора:
электродная пара датчика: индикаторный угольный трубчатый электрод с внутренним диаметром 0,1 см, длиной 3 см и вспомогательный — насыщенный хлорcеребряный электрод ЭВЛ- 1- МЗ;
фоновый электролит (подвижная фаза) — 0,1 М натрий ацетатный буфер, рН 3,8–4,0 и 0,3 М по KCI;
скорость течения подвижной фазы 100–120 см3/час;
объем вводимой пробы 0,1 см3.
Литература:
- Ruzicka J. The Second Coming of Flow-Injection Analysis // Anal. chim. acta. — 1992. — Vol. 261. — № 1/2. — P. 3–21.
- Siangproh W., Leesutthipornchai W., Dungchai W., Chailapakul O. Electrochemical Detection for Flow-based System: A Review // J. Flow Injection Anal.. — 2009. — Vol. 26. -No. 1. — Р. 5–25.
- Storck A., Enriques-Granados M. A., Roger M., Coeuret F. The behaviour of porous electrodes in a flow — by regine-1// Electro-chem. Acta — 1982. — V. 27, No. 2. — P. 293–301.
- Strohl A. N., Curran D. J. Reticulated vitreous carbon flow-throughi electrodes// Anal.Chem. — 1979. — V. 51, No. 3. — P. 353–357.
- Tougas T. P., Janetti J. M., Collier W. G. Theoretical and experimental response of a biamperometric detector for flow injection analysis// Anal.Chem. — 1985. — V. 57, No. 7. — P. 1377–1381.
- Wang J., Dewald H. D. A porous-jet flow-through electrode// Talanta — 1982. — V. 29, No. 6. — P. 453–456.
- Аронбаев Д. М. Кинетика и механизм электрохимического восстановления йода из водных растворов на угольных электродах // Мол.ученый. — 2015. — № 15–2(89). — С.
- Кольтгоф И. М., Сендел Е. Б. Количественный анализ. 3-е изд. — М.: Госхимиздат, 1948- 822 с.
- Кузнецов В. В. Проточно-инжекционный анализ //Соросовский образовательный журнал. — 1999. — № 1. — С.56–60.
- Левич В. Г. Физико-химическая гидродинамика. -М.: Физматгиз,1959. — С. 118–127.
- Чизмаджев Ю. А.,Чирков Ю. Г. Пористые электроды. // В кн.: Кинетика сложных электрохимических реакций. — М.: Наука,1981.- С.240–305.
- Чизмаджев Ю. Ф., Маркин В. С., Тарасевич М. Р., Чирков Ю. Г. Макрокинетика процессов в пористых средах. –М.: Наука, 1971.- 363с.
- Шпигун Л. К. Проточно-инжекционный анализ // Журн. аналит. химии. — 1990. — Т. 45, № 6. — С. 1045–1091.
- Шпигун Л. К., Золотов Ю. А. Проточно-инжекционный анализ. — М.: Знание, 1990. — 42 с.
- Яворский Б. М., Детлаф А. А. Справочник по физике для инженеров и студентов вузов. — М.: Наука, 1968.- С.332.