Степенные функции играют ключевую роль в моделировании биологических процессов, позволяя точно описать динамику роста популяций, метаболизма организмов и др. Рассмотрим такие популярные модели, как логистическая модель роста популяции и ее вариация без ограничения ресурсов, а также модель метаболизма и физиологии организма (закон Клейбера).

1. Моделирование роста популяции

Рост численности биологической популяции часто подчиняется закону экспоненциального роста, однако на практике этот процесс ограничен ресурсами среды обитания. Широкое применение нашли логистическая модель (1) с ограниченными ресурсами среды обитания [1] и ее упрощенный вариант (2) без ограничений ресурсов среды обитания [2].

В условиях ограничения ресурсами среды обитания применяется логистическая модель следующего вида:

, (1)

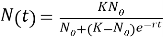
где:

— 𝑁(𝑡) — численность популяции в момент времени 𝑡;

— 𝐾 — максимальная емкость среды;

— 𝑁 _o — начальная численность;

— 𝑟 — внутренняя скорость прироста;

— e — основание натурального логарифма.

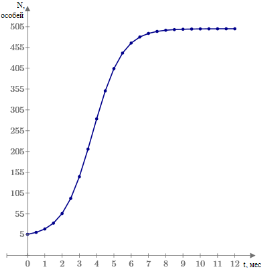
Пример графика, демонстрирующего модель (1), представлен на рисунке 1а. Начальными условиями в данном случае являются: t = 12 (мес.); 𝐾 = 700 (особей); 𝑁 _o = 6 (особей); 𝑟 = 1.17 (17 %/мес.).

В условиях отсутствия ограничения ресурсами среды обитания применяется логистическая модель следующего вида:

𝑁(𝑡)= N _o e ^rt . (2)

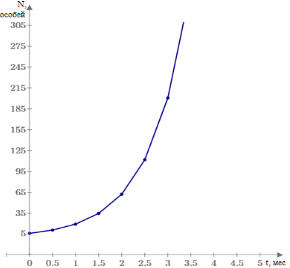
График ее функции, с начальными условиями равными: t = 12 (мес.), 𝑁 _o = 6 (особей); 𝑟 = 1.17 (17 %/мес.) показан на рисунке 1б. Рассматриваемая модель маловероятна для природных популяций и удобна в лабораторных условиях. Наиболее часто она используется для описания начальной стадии роста популяции, когда ограничения ресурсов еще не ощущаются — численность популяции растет в геометрической прогрессии, в то время как производство питания растет со временем в арифметической прогрессии.

Графики функции 𝑁(𝑡) получены самостоятельно в среде математического моделирования MatCAD Prime 4.0 [3].

Таким образом, рано или поздно наступит голод, в результате чего произойдет замедление скорости роста популяции и естественное ограничение ее численности.

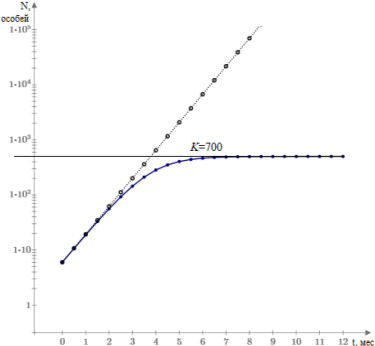
Рис. 2. Наложение графиков 1 а и 1 б

На рисунке 2 показано совмещение графиков функции роста популяции с ограниченными ресурсами и без (пунктирная линия), что наглядно демонстрирует разницу в моделях. Популяция, не испытывающая недостаток ресурсов, продолжает расти, но популяция, испытывающая недостаток — голод — перестанет численно увеличиваться, когда достигнет значения максимальной емкости среды (в данном примере максимальная емкость среды K =700).

2. Метаболизм и физиология организма

Важнейшим аспектом моделирования роста популяции является закон Клейбера (метаболический закон 3/4) — биохимическое правило, связывающее скорость основного обмена и массу организма [4].Закон сформулировал швейцарский учёный Макс Клейбер на основе наблюдений, сделанных в начале 1930-х годов.

Согласно закону, для подавляющего большинства животных скорость основного обмена (минимальное количество энергии, расходуемое организмом для поддержания жизнедеятельности в состоянии покоя)пропорциональна массе их организма в степени 3/4:

,

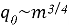
где:

— — обмен веществ животного в состоянии покоя;

— — масса тела животного.

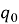
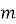
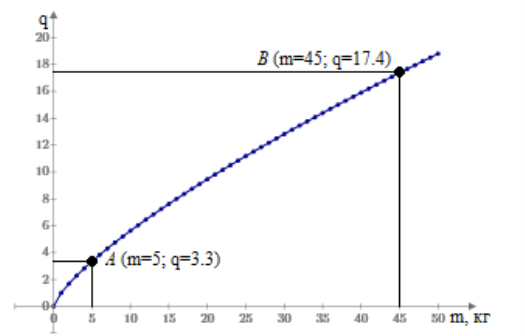
Рис. 3. График метаболизма и физиологии организма (закон Клейбера )

Этот закон гласит, что для большинства животных скорость обмена веществ пропорциональна массе их организма в степени 3/4. Например, если масса кошки в 100 раз больше массы мыши, то обмен веществ у кошки только в 32 раза больше, следовательно, по мере роста массы скорость метаболизма растёт всё медленнее. Это происходит из-за того, что у более крупных зверей поверхность тела на единицу объёма меньше, чем у мелких, различной плотности сосудов и разного количества капилляров, площади диффузии.

Заключение

Применение степенных функций в биологии позволяет создавать модели, помогающие лучше понять механизмы развития и функционирования живых организмов. Эти методы активно используются биологами, экологами и медицинскими специалистами для изучения широкого спектра вопросов, начиная от динамики популяций и заканчивая оценкой влияния окружающей среды на здоровье человека.

Литература:

1. Базыкин А. Д. Нелинейная динамика взаимодействующих популяций, Ижевск: Институт компьютерных исследований, 2003.
2. Братусь А. С., Новожилов А. С. Математические модели экологии и динамические системы с непрерывным временем, М.: МГУ, 2004.
3. Математические расчёты в среде Mathcad, А. А. Черняк, Ж. А. Черняк (3-е изд., испр. и доп.) — учебник для вузов, Москва: Издательство «Юрайт», 2025. ISBN 978–5-534–14675–2.
4. Семенова Е. Е. Математические методы в экологии: Сборник задач и упражнений / Е. Е. Семенова, Е. В. Кудрявцева. — Петрозаводск: Изд. ПетрГУ, 2005.