Спирограф



Спирограф представляет собой набор, состоящий из внешней дуги, по которой двигаются круги разного диаметра с отверстиями. Он позволяет изображать разные кривые. Их всех объединяют некоторые общие свойства. Пусть внутри круга или на продолжении его радиуса отмечена точка. При движении без скольжения по прямой она будет описывать некоторую кривую. Общее название данного класса кривых — трохоида. Спирограф используется для оформительских, мозаичных и чертежных работ, для вычисления площадей, ограниченных кривыми, для развития моторики и координации движений (у детей и в период реабилитации больных), для развития пространственного воображения. Отечественные исследователи дошкольный педагогики рассматривают целый спектр возможностей применения спирографа, касающихся подготовки (социальной, психологической, познавательной) ребенка дошкольника к обучению в школе. Спирограф также можно использовать в арт терапии. Автор не ограничился теоретическим изучением спирографа, но написал программный код и создал модель спирографа. Эта модель используется на уроках рисования, в работе кружка по черчению и по занимательной математике.

Ключевые слова: математические основы спирографа, гипотрохоида, гипоциклоида, эпитрохоида, роботизированное устройство, код на языке Pyhton.

Окружающие нас предметы не могут быть изображены на чертежах или рисунках с помощью прямых линий. Формы предметов содержат элементы кривых линий и поверхностей. Много знаний человечество накопило о кривых линиях: от улитки Паскаля до автоподобных фигур и фракталов, но в начертательной геометрии незаменимым прибором для вычерчивания кривых по-прежнему остается лекало. Однако, есть не менее интересный прибор для построения кривых. Это спирограф. Спирограф представляет собой набор, состоящий из внешней дуги, по которой двигаются круги разного диаметра с отверстиями. Изучение математических основ работы спирографа позволило автору разработать роботизированное устройство, которое используют не только на уроках рисования, но и для проведения исследований в разных областях наук (геометрии, черчении, архитектуре, генетике и др.).

В 1827 году инженер Питер Хьюберт Десвинь разработал устройство «Speiragraph» для создания сложных спиральных рисунков. Готовый макет он представил в 1845–1848 годах в Вене. Предполагалось, что данное устройство будет использоваться для защиты банкнот от подделки, так как любую созданную им кривую было сложно предугадать (рис1). Далее идея Хьюберта использована в начале 19 века при разработке токарного станка с гильошировкой для печати банкнот и почтовых марок. Прибор мог создавать пересекающиеся и переплетающиеся узоры различной формы. Станок использовался многими национальными монетными дворами. Более «игрушечная» версия станка впервые появилась в 1908 году в каталоге Sears. Статья, описывающая, как сделать такой станок, появилась в издании Boys Mechanic в 1913 году (рис.2).

Рис. 1. Образцы кривых

Рис. 2. Станок Wondergraph

Окончательно спирограф был представлен как детская игрушка в 1965 году Денисом Фишером, который в 1962 работал над взрывателями для авиабомб. Понадобилось устройство, которое могло бы начертить плавно изгибающиеся линии. Созданный спирограф не решил проблему, но понравился его детям, поэтому был адаптирован под игрушку. С 1965 по 1969 годы спирограф признан лучшей обучающей игрушкой. Он развивает воображение, мышление, даёт возможность реализовывать способность к рисованию, тренирует моторику рук, способствует увеличению скорости письма и улучшению почерка. При создании узора появляется множество вариантов разнообразить итоговый рисунок. Можно поменять цвет карандаша или ручки, сменить радиус колеса и добавить в рисунок другую фигуру, можно менять дальность отведения карандаша от центра окружности, что тоже влияет на результат.

Каковы математические основы работы спирографа? Пусть внутри круга или на продолжении его радиуса отмечена некоторая точка. При движении без скольжения по прямой она будет описывать некоторую кривую. Общее название данного класса кривых — трохоида. Если направляющая — прямая линия, то трохоида является циклоидой, если направляющая круг, то трохоида будет являться гипотрохоидой (качение происходит по внутренней стороне направляющего круга) или эпитрохоидой (качение происходит по внешней стороне направляющего круга). Трохоиды задаются системой уравнений (1.1):

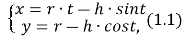
где h — расстояние точки от центра окружности, r — радиус окружности; окружность катится по прямой, совпадающей с горизонтальной осью координат. Если h = r, то трохоида называется циклоидой. Если h < r, то кривая называется укороченной циклоидой. Если h > r, то кривая называется удлиненной циклоидой.

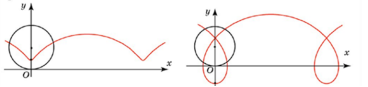
Рис. 3. . Графики укороченной и удлиненной циклоид

Фигуры, нарисованные спирографом, являются трохоидами, завёрнутыми или развёрнутыми в круг. Простейшая фигура (гипотрохоида), нарисована спирографом, состоящим из 2-х кругов, один с маленьким радиусом (внутри), второй с большим радиусом (снаружи). Гипотрохоида — завёрнутая в круг трохоида (рис.4). Плоская кривая задаётся параметрическим уравнением (1.2) в декартовой (прямоугольной) системе координат:

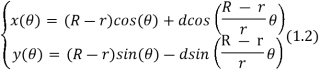
где R — радиус статической окружности; r — радиус динамической окружности;

d — длина от центра динамической окружности до точки черчения; θ — угол, образованный горизонталью и внутренней окружности.

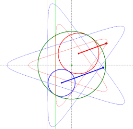
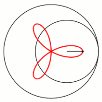
Рис. 4. Графики гипотрохоид

При измерении в радианах область значений угла ограничивается. θ принимает значения от 0 до значения, высчитываемого при помощи формулы (1.3):

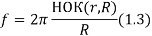
R — радиус внешней окружности; r — радиус внутренней окружности; f — максимальное значение для θ; НОК (значение 1, значение 2) — наименьшее общее кратное. Существует частный случай — гипоциклоида (рис.5). Она образуются, когда радиус статического круга равен радиусу динамического круга, умноженного на определённый коэффициент — k. Формула (1.4) принимает вид:

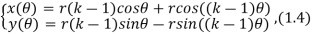
где r — радиус динамической окружности; θ — угол, образованный горизонталью и радиусом внутренней окружности; k — коэффициент, равный отношению радиуса внешнего круга к внутреннему: k=R/r. По рис. 5 можно сделать вывод, что k — количество точек касания фигуры с внешней окружностью, когда k — натуральное число, и фигура не выходит за пределы статической окружности.

Рис. 5. Графики гипоциклоид с натуральным значением k

У гипоциклоид есть своё название. Если k = 3, то фигура называется дельтоидой, если k = 4 — фигура называется астроидой. Если же коэффициент k — конечная десятичная дробь, то фигуры будут выглядеть по-другому.

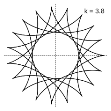
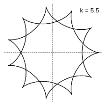
Рис. 6. Графики гипоциклоид при значениях k — конечной десятичной дроби

Вторая фигура, образованная спирографом, состоящим из 2-х кругов: с маленьким радиусом (снаружи), с большим радиусом (внутри). Такая фигура называется эпитрохоидой. Эпитрохоида — это трохоида, развёрнутая в круг. Эпитрохоида (рис.7) задается формулами (1.2, 1.3), как гипотрохоида.

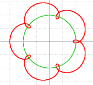
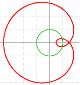
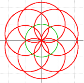
Рис. 7. Графики эпитрохоид: удлиненная, улитка Паскаля, Роза

Существует частный случай эпитрохоиды, называемый эпициклоидой. Он образуется, если радиус катящейся окружности равен расстоянию от центра этой окружности до точки, которая рисует фигуру. Формула (1.6) будет принимать следующий вид:

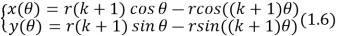
где r — радиус динамической окружности; k — коэффициент (1.5); θ — угол, образованный горизонталью и внешней окружностью. Коэффициент k — количество точек соприкосновения фигуры со статической окружностью, при этом коэффициент k — натуральное число.

Основываясь на этих математических законах, автор статьи разработал устройство «Спирограф» на платформе Arduino Uno. Рассмотрим подробнее конструкцию разработанного устройства. Плата Arduino Uno является самым важным элементом в конструкции спирографа, на базе которого работает вся электронная часть. С ее помощью программируется устройство. К ней подключена плата расширения Troyka Shield, которая увеличивает число пинов для подключения датчиков, моторов, узлов. К плате Troyka Shield подключены два драйвера для шаговых двигателей. Они нужны для управления движением шаговых двигателей, направлением вращения и регулировкой числа шагов поворота двигателя. Один шаг считается за 1.8 градуса. Полный оборот двигателя происходит при выполнении 200 шагов. Для питания драйверов в батарейном отсеке есть литий-ионные аккумуляторы форм-фактора 18650. Второй важный элемент — шаговый двигатель 42STH60–1206A. В модели использовались 2 двигателя. Третьим элементом является сервопривод постоянного вращения. Он нужен, чтобы вращать платформу, на которой будет рисовать спирограф. Помимо электрической части, для спирографа была разработана конструкция, которая удерживает и передвигает элемент для рисования. Данные детали соединяются с двигателями. Пластиковые детали для передачи вращения двигателя в поступательные движения представляют собой:

– две шайбы с одним центральным отверстием и отверстиями, располагающимися на разном расстоянии от центра окружности;

– два луча с отверстиями; на одном из лучей на малом расстоянии от крайнего есть отверстие, которое будет соединено с крайним отверстием другого луча.

В центральное отверстие шайб закрепляется вал двигателя, а к остальным отверстиям закрепляются лучи, чтобы регулировать размер получившейся кривой. Чтобы рисунок без изменений параметров движения спирографа был всегда одинаковый, надо сделать корпус, который соединяет и фиксирует на определенном расстоянии два двигателя. 3D-модели элементов данной конструкции были созданы в САПР «Компас-3D» и напечатаны на 3D-принтере с использованием PLA-пластика.

Рис. 8. Печать конструктивных элементов устройства

Далее дана схема подключения шагового двигателя с использованием драйвера и сервопривода к плате расширения (2-й двигатель подключается аналогично):

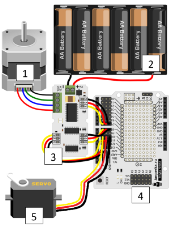
Рис. 9. Схема подключения шагового двигателя. На схеме цифрами обозначены: 1 — шаговый двигатель; 2- аккумуляторный отсек с литий-ионными батарейками; 3 — драйвер для шагового двигателя; 4 — плата расширения Troyka Shield; 5 — сервопривод постоянного вращения

Тестовый стенд представлен на рисунке 10. В качестве корпуса для сервопривода и основы для поворотного столика был использован «#структор», изготовленный из вспененного ПВХ. Сверху на сервопривод прикреплена основа вращающегося стола, где закреплён лист бумаги.

Рис. 10. Устройство «Спирограф» в сборке

Программирование устройства на платформе Arduino Uno осуществляется в среде разработки Arduino IDE на языке wiring (C++ с дополнительными модулями и библиотеками).

Основные блоки программного кода (скетча) работы устройства:

1. Подключение необходимых библиотек для работы с сервоприводами.
2. Создание объекта для работы с сервоприводом.
3. Объявление переменных, отвечающих за регулировку скорости вращения и переменных, содержащих направление вращения механических элементов.
4. Создание переменных для хранения пути к сервоприводу и двигателям.
5. Настройка пинов, к которым подключены элементы.
6. Корректировка рисунка изменением скорости и направления вращения мотора.

Алгоритм построения изображения основан на циклично повторяющихся действиях шаговых двигателей и сервопривода. В коде установлено постоянное вращение сервомотора и скорость вращения двигателей. При выполнении заданного количества шагов, направление движения двигателей изменяется.

Функционирование блоков

1. Сервопривод.

– подключаем библиотеку для использования сервопривода: AmperkaServo.h

– создаём объект, над которым будет вестись управление: AmperkaServo servo;

– задаём имя пина, к которому подключен сервомотор: SERVO_PIN = 10;

– подключение сервомотора с параметрами: minPulseWidth, maxPulseWidth — минимальная и максимальная ширина импульса в соответствии с максимальной скоростью вращения по часовой и против часовой стрелки. В блоке void setup (), где производится установка режимов работы и инициализация устройств, указываем: servo.attach(SERVO_PIN, 544, 2400);

– в основном блоке — бесконечном цикле void loop () — надо задать скорость вращения сервопривода: servo.writeSpeed(50);

2. Шаговые двигатели (на примере одного из двух).

– объявляем константы, которые хранят в себе пин, к которому подключён шаговый двигатель: stepPin = 7; directionPin = 8; enablePin = 11;

– объявляем переменную регулировки скорости двигателя: delayTime = 3;

– в блоке void setup() настраиваем нужные контакты на выход сигнала, подаём питание на двигатель и настраиваем изначальное направление вращения:

pinMode(stepPin, OUTPUT); pinMode(directionPin, OUTPUT); pinMode(enablePin, OUTPUT);

digitalWrite(enablePin, HIGH); digitalWrite(directionPin, true);

Чтобы шаговый двигатель сделал поворот на 1.8 градуса, нужно подать напряжение на двигатель и остановить подачу. Магниты внутри двигателя притягивают к себе ротор, делая один поворот, и выключаются. Подача напряжения происходит на пин — «stepPin», в параметрах указывается значения — HIGH или LOW. HIGH — подача напряжения 7.2 В (логическая единица), LOW — подача напряжения 0 В (логический ноль). Еще надо выставить задержку между подачами напряжения (управление скоростью вращения) при помощи встроенной функции delay(), в параметрах указывается переменная delayTime. В алгоритм добавлено условие для смены направления вращения шагового двигателя при выполнении 100 шагов или поворота на 180 градусов. Счётчиком выполненных шагов является переменная k, объявленная в начале программы, с каждым шагом к ней добавляется единица. В алгоритм можно встроить динамическое изменение скорости вращения двигателя при помощи счётчика. И все действия надо повторить для второго двигателя, но с другими переменными и условиями. Далее приведен полный скетч с некоторыми комментариями:

Рис. 11

Чтобы проанализировать работу созданного устройства и сопоставить создаваемые им рисунки с теми, которые должны получаться по формулам при определенных параметрах, было разработано приложение на языке Python. Полный код приложения можно увидеть по ссылке: https://github.com/raidfb/Project---Spirograph.

В языке программирования Python существует библиотека для работы с графикой. Turtle graphics — реализация популярных инструментов геометрического рисования. На ее основе создают спирограф, с помощью которого можно подбирать параметры для тестового стенда. В программном коде есть функции для настройки параметров фигуры, параметры для ручки и окна, в которое выводится результат. Спирограф рисует фигуру при помощи решения параметрического уравнения (1.2), вот так уравнение выглядит в коде:

R — радиус внешней окружности; r — радиус внутренней окружности; d — расстояние от рисующей точки до центра внешней окружности; angle — угол, который с каждым выполнением цикла добавляет значение. При уменьшении величины угла усиливается точность рисовки фигуры.

При помощи пяти команд можно нарисовать любой объект в графике Turtle:

– turtle.pendown() — опускает ручки для начала рисования

– turtle.goto(x,y) — перемещает ручки по заданным координатам

– turtle.penup() — поднимает ручку для прекращения рисования

– turtle.getscreen().update() — обновляет экран

– window.mainloop() — зацикливает картинку при выполнении всех команд

Прошло тестирование работы шаговых двигателей по написанному алгоритму вращения двух моторов в разные стороны. При выполнении данного кода получена фигура (рис.12 а). Сдвиг ручки в основном обусловлен сдвигом моторов от вибрации. Данный рисунок не напоминает фигуру, нарисованную спирографом. Но если добавить вращающийся стол, то получится фигура, которая очень похожа на фигуру, образованную спирографом.

Фигура (рис.12 б) была образована при данных параметрах:

– servo.writeSpeed(50); — скорость вращения сервопривода равно значению 50;

– int delayTime1 = 3; — выдержка для регулировки скорости 1;

– int delayTime2 = 3; — выдержка для регулировки скорости 2;

– использован цикл, который меняет направление вращения каждый 101 шаг.

Получившаяся фигура также похожа на фигуру (рис.12 в), нарисованную при помощи приложения на Python при следующих параметрах:

– R — внешней окружности (125);

– r — внутренней окружности (45);

– d — расстояние от рисующей точки до центра внешней окружности (125).

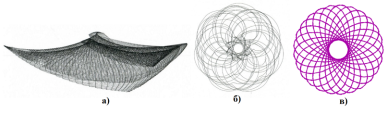
Рис. 12. Изображения, созданные спирографом (а,б) и в программе (в)

В дальнейшем планируется отладить прибор так, чтобы получилось совместить график, построенный программой на Python, с физическим устройством, а также сделать интерфейс для работы с программой устройства. Для этого надо провести много тестов и адаптировать код, исходя из полученных закономерностей. При этом программный код устройства будет дополнен, чтобы рисовать несколькими спирографами по элементам на одном листке. Так можно будет изобразить фигуру, которая задается математической формулой, но при этом расшифровать эту формулу очень сложно.

Литература:

1. Амперка. База знаний (wiki) — URL: https://wiki.amperka.ru/
2. Спирограф как одна из самых высокоинтеллектуальных игр 20 века — URL: https://7centr.ru/wp-content/uploads/2015/09/Spirograf-kak-odna-iz-samyh-vysokointellektualnyh-igr-20-veka-10062020062324.pdf
3. Спирограф (игрушка) — URL: https://ru.wikipedia.org/wiki/Спирограф_(игрушка)
4. Трохоида — URL: https://ru.wikipedia.org/wiki/Трохоида
5. Гипотрохоида — URL: https://ru.wikipedia.org/wiki/Гипотрохоида
6. Гипоциклоида — URL: https://ru.wikipedia.org/wiki/Гипоциклоида
7. Эпитрохоида — URL: https://ru.wikipedia.org/wiki/Эпитрохоида
8. Эпициклоида — URL: https://ru.wikipedia.org/wiki/Эпициклоида
9. Простое устройство на Arduino для рисования сложных паттернов — URL: https://robocraft.ru/projects/4216
10. Arduino Powered Pattern Making Machine — URL: https://www.instructables.com/Arduino-Powered-Pattern-Making-Machine/